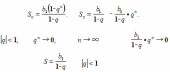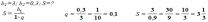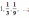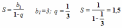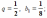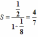| Краткосрочный план № 37 | ||
| Раздел долгосрочного плана: Раздел: Последовательности | Школа: Архиповская СШ | |
| Дата: 04.12.19 | ФИО учителя: Тарасенко Е. Л. | |
| Класс: 9 | Количество присутствующих: | отсутствующих: |
| Тема урока | Бесконечно убывающая геометрическая прогрессия | |
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 9.2.3.8 применять формулу суммы бесконечно убывающей геометрической прогрессии для перевода десятичной периодической дроби в обыкновенную дробь; | |
| Цели урока | Учащиеся будут:
| |
| Критерии оценивания |
| |
| Языковые цели | Учащиеся будут:
Предметная лексика и терминология
Серия полезных фраз для диалога/письма
| |
| Межпредметные связи | геометрия, экономика | |
| Предварительные знания | Числовая последовательность, арифметическая прогрессия, геометрическая прогрессия |
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Краткосрочный план урока на тему "Бесконечно убывающая геометрическая прогрессия".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Краткосрочный план урока на тему "Бесконечно убывающая геометрическая прогрессия".»
Полезное для учителя
Распродажа видеоуроков!
1220 руб.
1740 руб.
1950 руб.
2780 руб.
2030 руб.
2900 руб.
1700 руб.
2430 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
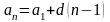
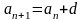 )
)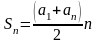 или
или 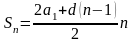 )
)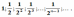 образующих геометрическую прогрессию со знаменателем
образующих геометрическую прогрессию со знаменателем 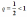 .
.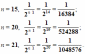
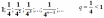 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.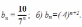

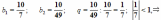 данная геометрическая прогрессия является бесконечно убывающей.
данная геометрическая прогрессия является бесконечно убывающей.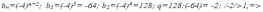 данная последовательность не является бесконечно убывающей геометрической прогрессией.
данная последовательность не является бесконечно убывающей геометрической прогрессией.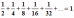 Но в левой части этого равенства – сумма бесконечного числа слагаемых. Рассмотрим сумму n первых слагаемых.
Но в левой части этого равенства – сумма бесконечного числа слагаемых. Рассмотрим сумму n первых слагаемых. 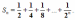 По формуле суммы n первых членов геометрической прогрессии, она равна
По формуле суммы n первых членов геометрической прогрессии, она равна 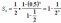 . Если n неограниченно возрастает, то
. Если n неограниченно возрастает, то 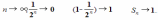
 . Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии. Рассмотрим формулу n первых членов геометрической прогрессии.
. Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии. Рассмотрим формулу n первых членов геометрической прогрессии.