Урок алгебры в 8 классе по теме "Площади фигур на клетчатой бумаге". Применение формул площадей квадрата, прямоугольника, треугольника и формулы Пика.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Площади фигур на клетчатой бумаге
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Площади фигур на клетчатой бумаге»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1650 руб.
2350 руб.
1760 руб.
2520 руб.
1370 руб.
1960 руб.
1620 руб.
2320 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

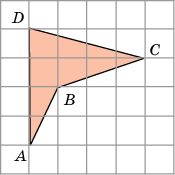 зобьем фигуру АВСD на части (1, 2, 3 и 4).
зобьем фигуру АВСD на части (1, 2, 3 и 4).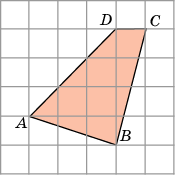 адача 3. Найдём площадь фигуры АВСD . Если клетки размером 1х1см.
адача 3. Найдём площадь фигуры АВСD . Если клетки размером 1х1см.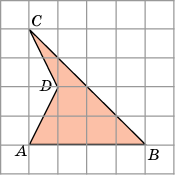 пишем около фигуры АВСD прямоугольник.
пишем около фигуры АВСD прямоугольник.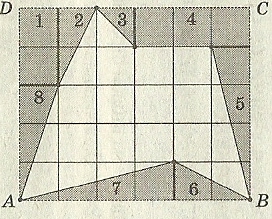 инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.
инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. ик .
ик .
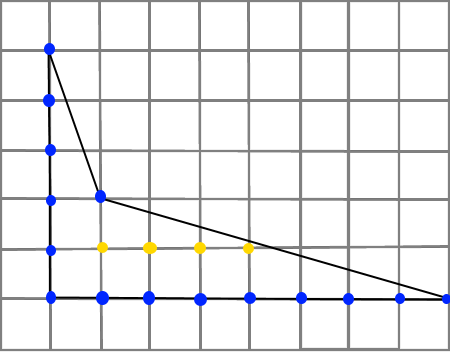
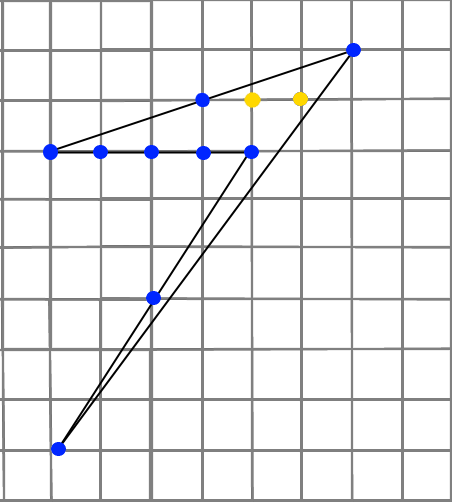
 метим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:
метим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника: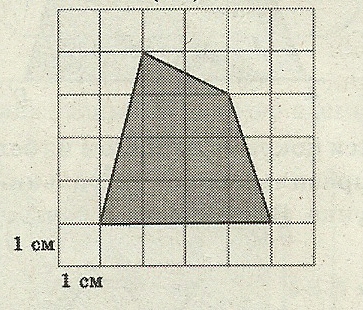 йдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В +
йдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В + 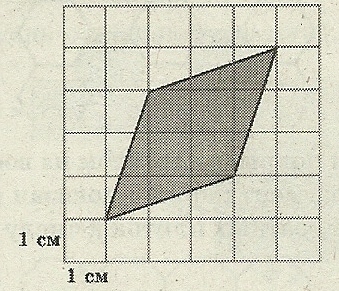 адача 4. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м .
адача 4. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м .