Данная работа представляет из себя презентацию с условием задач и предложенной технологией их решения по теме "Логика". Рассматриваются четыре вида задач. Материал поможет учителю при подготовке к ОГЭ выпускников 9 класса. Также может быть использован педагогом и для организации самостоятельной работы учащихся.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
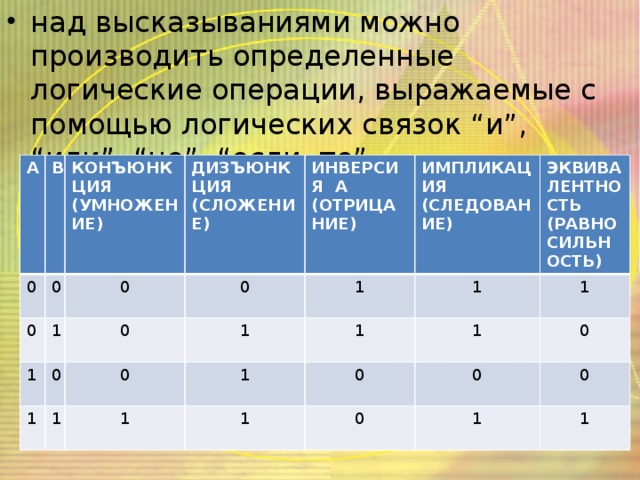
Логика в заданиях ОГЭ по информатике.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Логика в заданиях ОГЭ по информатике. »
Полезное для учителя
Распродажа видеоуроков!
1440 руб.
2060 руб.
1670 руб.
2390 руб.
1700 руб.
2430 руб.
1410 руб.
2020 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
















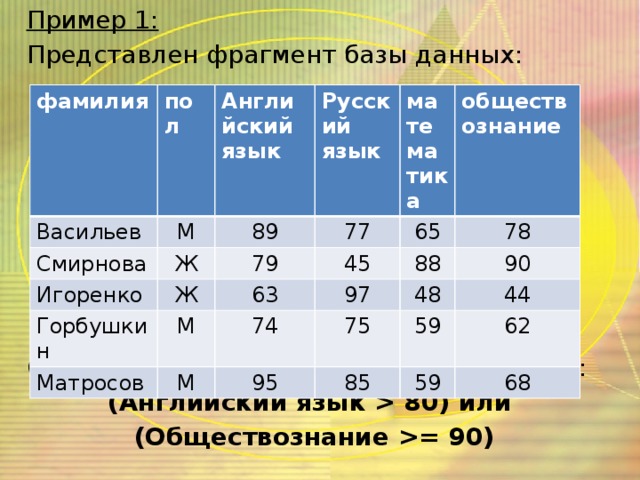 80) или (Обществознание = 90) фамилия Васильев пол Английский язык Смирнова М Русский язык Игоренко 89 Ж 79 Ж 77 математика Горбушкин 65 45 обществознание 63 Матросов М 78 88 97 74 М 48 90 75 95 44 59 85 62 59 68" width="640"
80) или (Обществознание = 90) фамилия Васильев пол Английский язык Смирнова М Русский язык Игоренко 89 Ж 79 Ж 77 математика Горбушкин 65 45 обществознание 63 Матросов М 78 88 97 74 М 48 90 75 95 44 59 85 62 59 68" width="640"
 80) или (Обществознание = 90) примет значение ИСТИНА , если истинным будет хотя бы одно из двух высказываний. 2. Обозначим высказывание (Английский язык 80) - «А», высказывание (Обществознание = 90) - «В» и составим таблицу истинности" width="640"
80) или (Обществознание = 90) примет значение ИСТИНА , если истинным будет хотя бы одно из двух высказываний. 2. Обозначим высказывание (Английский язык 80) - «А», высказывание (Обществознание = 90) - «В» и составим таблицу истинности" width="640"
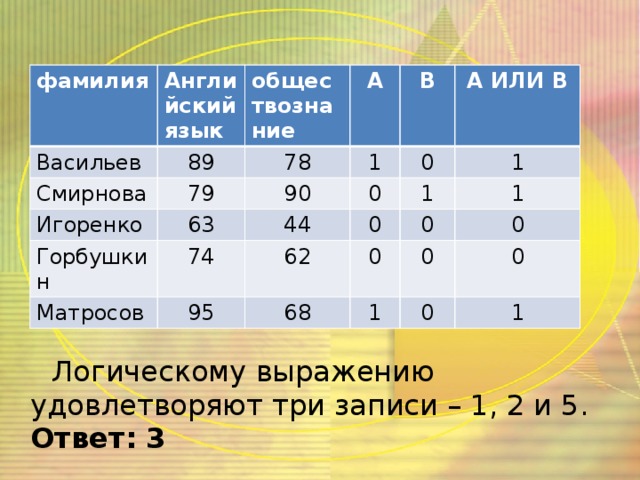
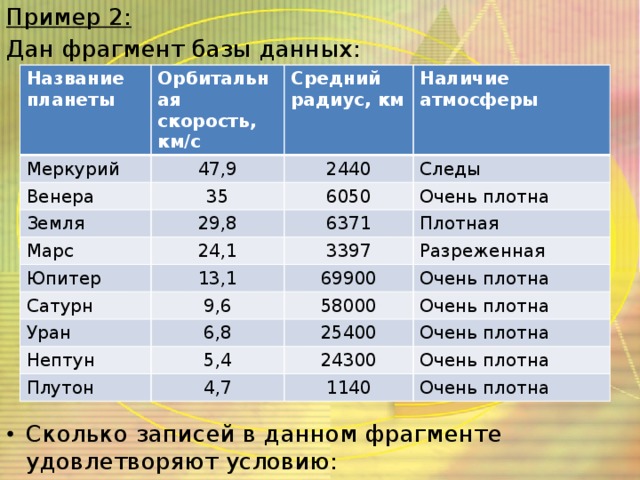
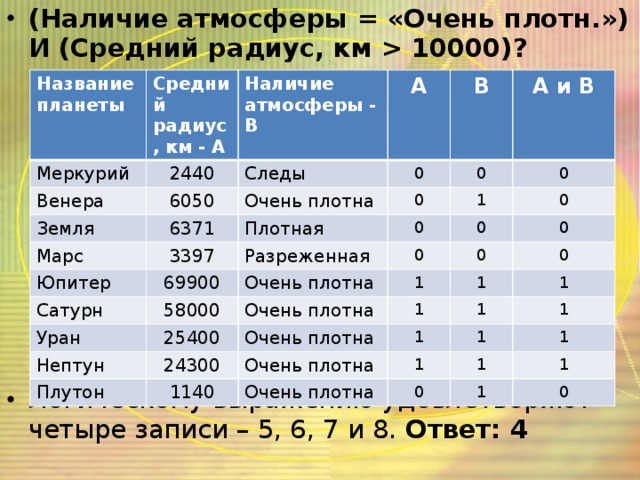 10000)? Логическому выражению удовлетворяют четыре записи – 5, 6, 7 и 8. Ответ: 4" width="640"
10000)? Логическому выражению удовлетворяют четыре записи – 5, 6, 7 и 8. Ответ: 4" width="640"





























