Появление компьютеров изменило все сферы современной науки и общественной, и даже личной, жизни. Появилась возможность проводить сложнейшие вычислительные эксперименты, что экономит не только деньги, но и время. Последнее обстоятельство особенно важно для научных работников, педагогов и студентов. Однако в нашей стране именно в области образования применение современных компьютерных методов и систем оставляет желать лучшего. Частично это связано с объективными причинами (дороговизна оборудования, программных продуктов и т. д.), однако очень часто и с субъективными — нежеланием что-либо менять, поскольку наше образование и так «самое лучшее в мире».
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Презентация на тему "Реализация рациональной арифметики в системах символьной математики"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация на тему "Реализация рациональной арифметики в системах символьной математики"»
Полезное для учителя
Распродажа видеоуроков!
1710 руб.
2440 руб.
1480 руб.
2110 руб.
1610 руб.
2300 руб.
1550 руб.
2220 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



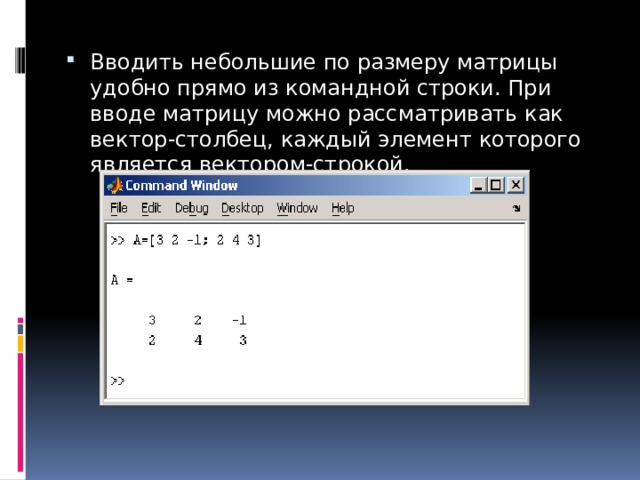
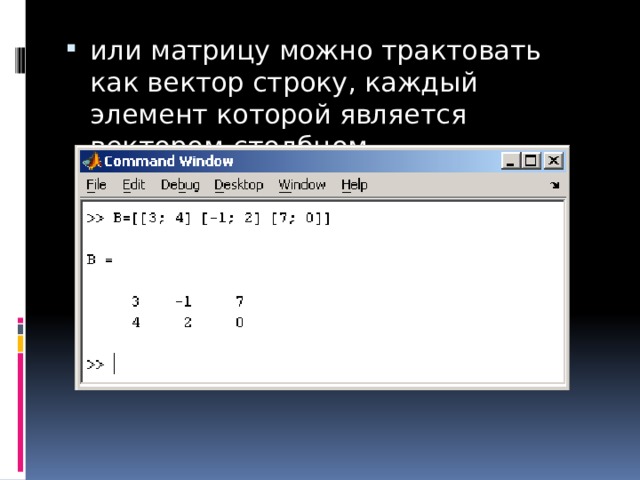
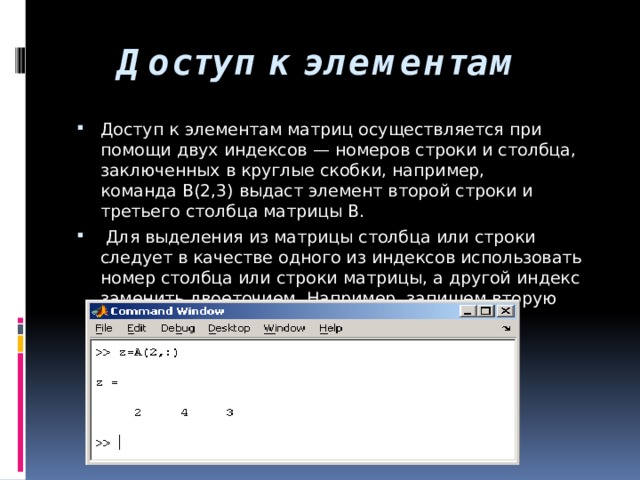
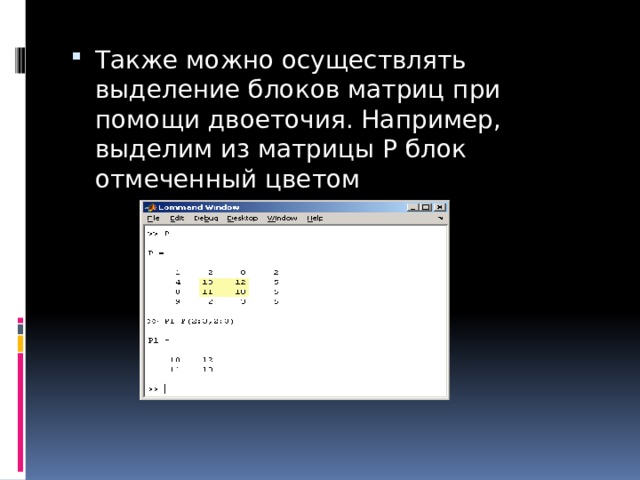
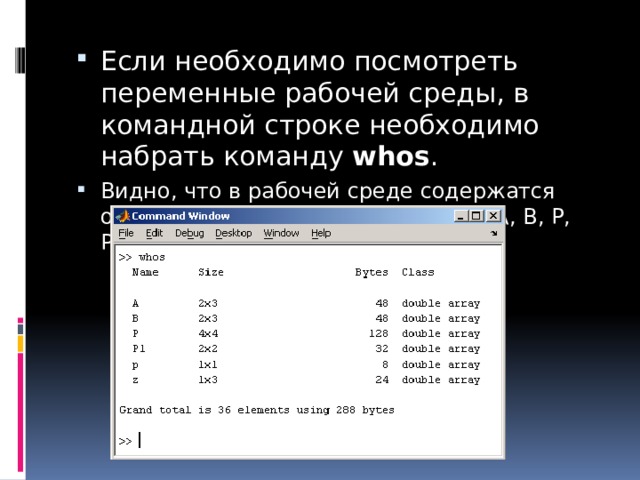
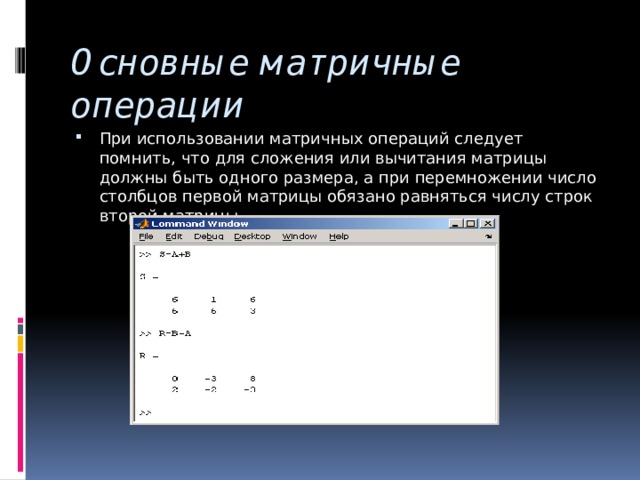
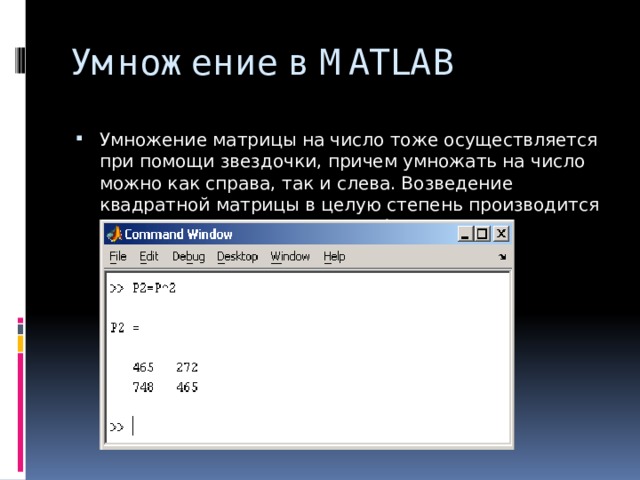
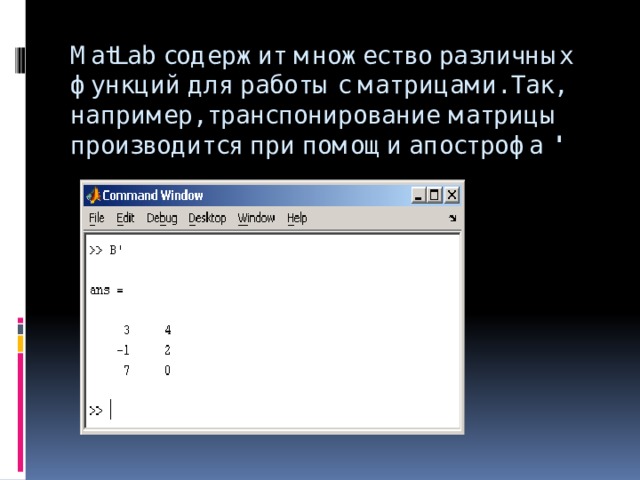
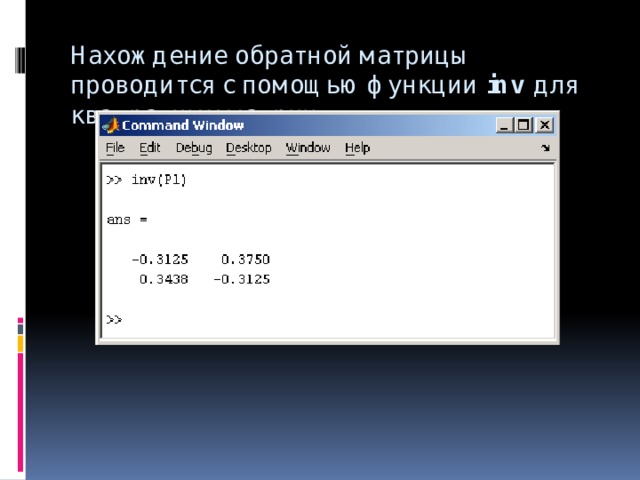
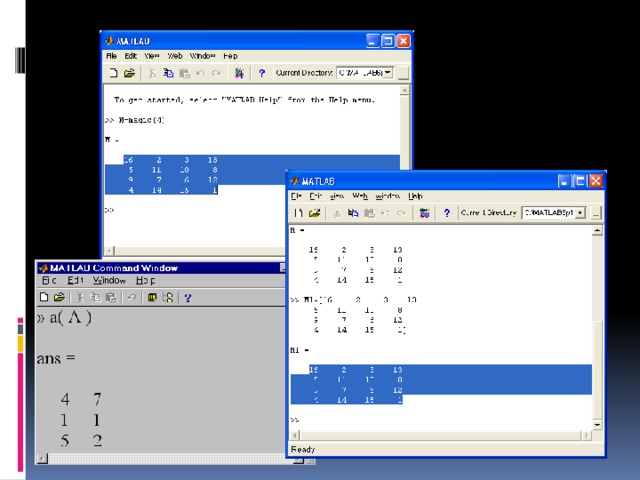

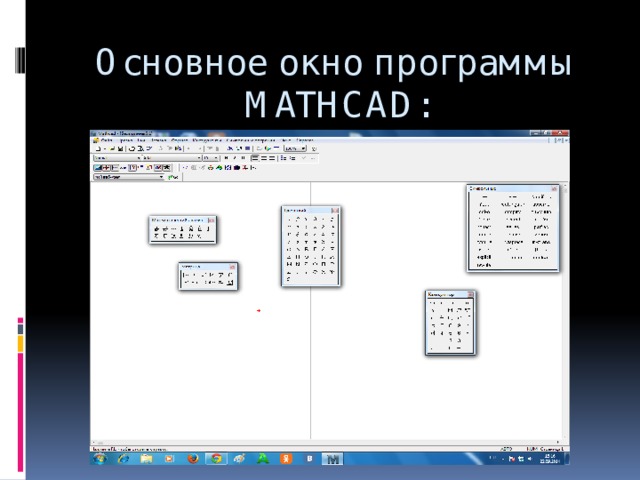

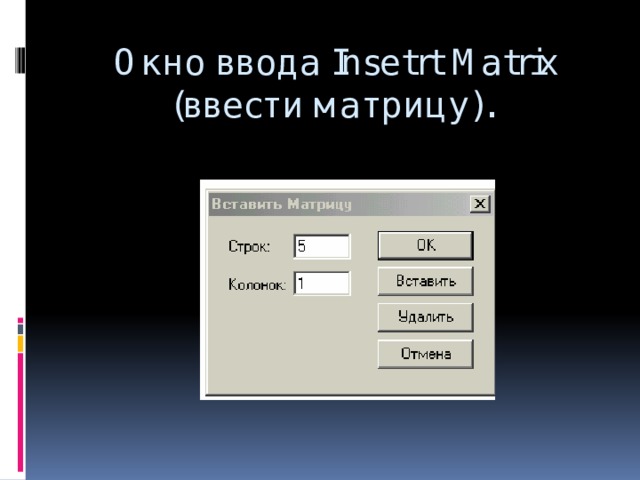





![Определение матрицы: matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…,[an1,an2,…,anm]]),](https://fsd.kopilkaurokov.ru/up/html/2020/03/24/k_5e7a398a554bf/img_user_file_5e7a398be154c_26.jpg)
 A:=matrix([[1,2,3],[-3,-2,-1]]);" width="640"
A:=matrix([[1,2,3],[-3,-2,-1]]);" width="640"
 J:=diag(1,2,3); 1 0 0 J:= 0 2 0 0 3 0" width="640"
J:=diag(1,2,3); 1 0 0 J:= 0 2 0 0 3 0" width="640"



 v:=vector([2,4]); v := [2,4] multiply(A,v); [2,−4]" width="640"
v:=vector([2,4]); v := [2,4] multiply(A,v); [2,−4]" width="640"
 С:=matrix([[1,1],[2,3]]): evalm(2+3*С); 5 3" width="640"
С:=matrix([[1,1],[2,3]]): evalm(2+3*С); 5 3" width="640"




















