Районная научно-исследовательская конференция школьников Лахденпохского муниципального района
«Шаг в будущее»
Проект по математике на тему:
«Признаки делимости натуральных чисел»
Выполнила: Галкина Наталья
ученица 7 класса
МКОУ «Элисенваарской СОШ»
Руководитель: Васильева
Лариса Владимировна
учитель математики
МКОУ «Элисенваарской СОШ»
2014 г.
Оглавление:
Введение 3 стр.
Из истории математики 4 стр.
Основные понятия 4 стр.
Классификация признаков делимости: 5 стр.
Делимость чисел определяется по последней(им) цифре(ам) 5 – 6 стр.
Делимость чисел определяется по сумме цифр числа: 6 стр.
Делимость чисел определяется после выполнения каких-то действий над цифрами числа 6 - 9 стр.
Для определения делимости числа используются другие признаки 9 – 10 стр.
Применение признаков делимости на практике 10 – 11 стр.
Заключение 11 стр.
Библиографический список 12 стр.
Введение
Актуальность исследования: Признаки делимости всегда интересовали ученых разных времен и народов. При изучении на уроках математики темы «Признаки делимости чисел на 2, 3, 5, 9, 10» у меня возник интерес к исследованию чисел на делимость. Было предположено, что если можно определить делимость чисел на эти числа, то должны быть признаки, по которым можно определить делимость натуральных чисел и на другие числа. В некоторых случаях, для того, чтобы узнать делится ли какое-либо натуральное число a на натуральное число b без остатка, не обязательно делить данные числа. Достаточно знать некоторые признаки делимости.
Гипотеза – если существуют признаки делимости натуральных чисел на 2, 3, 5, 9 и 10, то существуют и другие признаки, по которым можно определить делимость натуральных чисел.
Цель исследования – дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе и систематизировать эти признаки делимости.
Для достижения этой цели необходимо решить следующие задачи:
Объект исследования – изучение всевозможных признаков делимости.
Предмет исследования – признаки делимости.
Методы исследования – сбор материала, обработка данных, сравнение, анализ, обобщение.
Новизна: в ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Из истории математики
Блез Паскаль (родился в 1623 году) - один из самых знаменитых людей в истории человечества. Паскаль умер, когда ему было 39 лет, но, несмотря на столь короткую жизнь, вошел в историю как выдающийся математик, физик, философ и писатель. Его именем названы единица давления (паскаль) и весьма популярный сегодня язык программирования. Блез Паскаль нашёл общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число.
Признак Паскаля — метод, позволяющий получить признаки делимости на любое число. Своего рода «универсальный признак делимости».
Признак делимости Паскаля: Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.
Например: число 2814 делится на 7, так как 2·6+8·2+1·3+4=35 делится на 7. (Здесь 6-остаток отделения 1000 на 7, 2- остаток от деления 100 на 7 и 3- остаток от деления 10 на 7).
Основные понятия
Вспомним некоторые математические понятия, которые нам будут необходимы при изучении данной темы.
Признак делимости - это правило, по которому, не выполняя деления, можно установить, делится ли одно число на другое.
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Простыми называются натуральные числа, которые не имеют других натуральных различных делителей, кроме единицы и самого себя.
Составными называются числа, которые имеют и другие натуральные делители кроме 1 и самого себя.
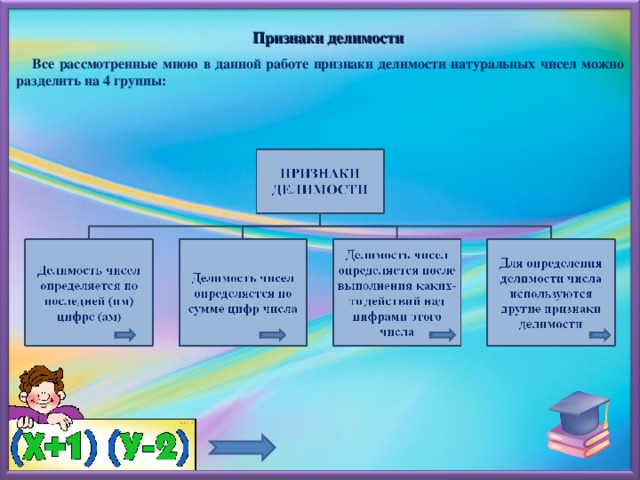
Признаки делимости
Все рассмотренные мною в данной работе признаки делимости натуральных чисел можно разделить на 4 группы:

Рассмотрим более подробно каждую из этих групп.
Делимость чисел определяется по последней (им) цифре (ам)
К первой группе рассмотренных мною признаков делимости натуральных чисел относятся признаки делимости на 2, 4, 5, 8, 20, 25, 50, 125 и разрядные единицы 10, 100 и т.д.
Признак делимости на 2: число делится на 2 тогда, когда последняя цифра этого числа делится на 2 (т.е. последняя цифра является чётным числом).
Например: 32217864 : 2
Признак делимости на 4: число делится на 4 тогда, когда две его последние цифры – нули, либо когда двузначное число, образованное двумя его последними цифрами, делится на 4.
Например, 35324 : 4; 6600 : 4
Признак делимости на 5: число делится на 5 тогда, когда его последняя цифра - 5 или 0.
Например: 36780 : 5 или 123265 : 5
Признак делимости на 8: число делится на 8 тогда, когда на 8 делится трехзначное число, образованное из трех последних цифр этого числа.
Например: 432240 : 8
Признак делимости на 20: число делится на 20 тогда, когда число, образованное двумя последними цифрами, делится на 20. (Другая формулировка: число делится на 20 тогда, когда последняя цифра числа — 0, а предпоследняя — чётная).
Например: 59640 : 20
Признак делимости на 25: на 25 делятся числа, две последние цифры которых нули или образуют число, которое делится на 25.
Например: 667975 : 25 или 7768900 : 25
Признак делимости на 50: число делится на 50 тогда, когда число, образованное двумя его младшими десятичными цифрами, делится на 50.
Например: 564350 : 50 или 554300 : 50
Признак делимости на 125: число делится на 125, если три его последние цифры нули или образуют число, которое делится на 125.
Например: 32157000 : 125 или 3216250 : 125
Признаки делимости на разрядную единицу 10, 100, 1000 и т.д.: на разрядную единицу делятся те натуральные числа, у которых количество нулей больше или равно количеству нулей разрядной единицы.
Например, 12 000 делится на 10, 100 и 1000.
Делимость чисел определяется по сумме цифр числа
К этой группе признаков делимости натуральных чисел относятся рассмотренные мною признаки делимости на 3, 9, 11.
Признак делимости на 3: число делится на 3, если его сумма цифр делится на 3.
Например: 5421 : 3 т.к. 5+4+2+1=12, (12:3)
Признак делимости на 9: число делится на 9, если его сумма цифр делится на 9.
Например: 653022 : 9 т.к. 6+5+3+0+2+2=18, (18:9)
Признак делимости на 11: на 11 делятся те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, кратное 11.
Например: 865948732:11 т.к. 8+5+4+7+2=26 и 6+9+8+3=26 (26=26); 815248742:11 т.к. 8+5+4+7+2=26 и 1+2+8+4=15, 26-15=11, (11:11)
Делимость чисел определяется после выполнения каких-то действий над цифрами этого числа
К этой группе признаков делимости натуральных чисел относятся признаки делимости на: 6, 7, 11, 13,17, 19, 23, 27, 29, 31, 33, 37, 41, 59, 79, 101
Признак делимости на 6:
Признак 1: число делится на 6 тогда, когда результат вычитания удвоенного числа сотен из числа, стоящего после сотен делится на 6.
Например, 138 : 6 т.к. 1·2=2, 38 – 2=36, (36:6); 744:6 т.к. 44 – 7·2=30, (30:6)
Признак 2: число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц делится на 6.
Например, 768:6 т.к. 76·4+8=312, 31·4+2=126, 12·4+6=54 (54:6)
Признаки делимости на 7:
Признак 1: число делится на 7 тогда, когда утроенное число десятков, сложенное с числом единиц, делится на 7.
Например, число 154:7, т.к. на 7 делятся 15·3 + 4 = 49 (49:7)
Признак 2: число делится на 7 тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по три цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 7.
Например, 138689257:7, т.к. ǀ138-689+257ǀ=294 (294:7)
Признаки делимости на 11:
Признак 1: число делится на 11 тогда, когда модуль разности между суммой цифр, занимающих нечётные позиции, и суммой цифр, занимающих чётные места делится на 11.
Например, 9163627:11, т.к. ǀ(9+6+6+7)-(1+3+2)ǀ=22 (22:11)
Признак 2: число делится на 11 тогда, когда на 11 делится сумма чисел, образующих группы по две цифры (начиная с единиц).
Например, 103785:11, т.к. 10+37+85=132 и 01+32=33 (33:11)
Признаки делимости на 13:
Признак 1: число делится на 13 тогда, когда сумма числа десятков с учетверенным числом единиц делится на 13.
Например, 845 :13, т.к. 84+5·4=104, 10+4·4=26 (26:13)
Признак 2: число делится на 13 тогда, когда разность числа десятков с девятикратным числом единиц делится на 13.
Например, 845 :13, т.к. 84-5·9=39 (39:13)
Признак делимости на 17: число делится на 17 тогда, когда модуль разности числа десятков и пятикратного числа единиц делится на 17.
Например, 221:17, т.к. ǀ22-5·1ǀ=17
Признаки делимости на 19: число делится на 19 тогда, когда число десятков, сложенное с удвоенным числом единиц, делится на 19.
Например, 646:19, т.к. 64+6·2=76, 7+2·6=19, (19:19)
Признаки делимости на 23:
Признак 1: число делится на 23 тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23.
Например, 28842:23, т.к. 288+3·42=414, 4+3·14=46 (46:23)
Признак 2: число делится на 23 тогда, когда число десятков, сложенное с семикратным числом единиц, делится на 23.
Например, 391:23, т.к. 39+7·1=46 (46:23)
Признак 3: число делится на 23 тогда, когда число сотен, сложенное с семикратным числом десятков и утроенным числом единиц, делится на 23.
Например, 391:23, т.к. 3+7·9+3·1=69 (69:23)
Признак делимости на 27: число делится на 27 тогда, когда на 27 делится сумма чисел, образующих группы по три цифры (начиная с единиц).
Например, 2705427:27 т.к. 427+705+2=1134, 134+1=135, (135:27)
Признак делимости на 29: число делится на 29 тогда, когда число десятков, сложенное с утроенным числом единиц, делится на 29.
Например, 261:29, т.к. 26+3·1=29 (29:29)
Признак делимости на 31: число делится на 31 тогда, когда модуль разности числа десятков и утроенного числа единиц делится на 31.
Например, 217:31, т.к. ǀ21-3·7ǀ= 0, (0:31)
Признаки делимости на 33: если сумма, составленная при разбивании числа справа налево на группы по две цифры, делится на 33, то и число делится на 33.
Например, 396:33, т.к. 96+3=99 (99:33)
Признаки делимости на 37:
Признак 1: число делится на 37 тогда, когда при разбиении числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 37.
Например, число 100048:37, т.к. 100+048=148, (148:37)
Признак 2: число делится на 37 тогда, когда на 37 делится модуль утроенного числа сотен, сложенного с учетверённым числом десятков, за вычетом числа единиц, умноженного на семь.
Например, число 481:37, так как на 37 делится ǀ3·4+4·8-7·1ǀ=37
Признаки делимости на 41:
Признак 1: число делится на 41 тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41.
Например, 369:41, т.к. ǀ36-4·9ǀ=0, (0:41)
Признак 2: чтобы проверить, делится ли число на 41, его следует справа налево разбить на группы по 5 цифр в каждой. Затем в каждой группе первую справа цифру умножить на 1, вторую цифру умножить на 10, третью — на 18, четвёртую — на 16, пятую — на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и само число будет делиться на 41.
Признак делимости на 59: число делится на 59 тогда, когда число десятков, сложенное с числом единиц, умноженное на 6, делится на 59.
Например, 767:59, т.к. 76+7·6=118, 11+8·6=59, (59:59)
Признак делимости на 79: число делится на 79 тогда, когда число десятков, сложенное с числом единиц, умноженное на 8, делится на 79.
Например, 711:79, т.к. 71+8·1=79, (79:79)
Признак делимости на 99: число делится на 99 тогда, когда на 99 делится сумма чисел, образующих группы по две цифры (начиная с единиц).
Например, 12573:99, т.к. 1+25+73=99, (99:99)
Признак делимости на 101: число делится на 101 тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по две цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «–» делится на 101.
Например, 590547:101, т.к. ǀ59-5+47ǀ=101, (101:101)
Для определения делимости числа используются другие признаки делимости
К этой группе признаков делимости натуральных чисел относятся признаки делимости на: 6, 12, 14, 15, 27, 30, 60 и т.д. Эти все числа - составные. Признаки делимости составных чисел строятся на признаках делимости простых чисел, на которые можно разложить любое составное число.
Признак делимости на 6:
Признак 1: число делится на 6 тогда, когда оно делится и на 2, и на 3, то есть, если оно четное и сумма его цифр делится на 3.
Например, 768:6, т.к. 7+6+8=21 (21:3) и последняя цифра в числе 768 – четная.
Признак делимости на 12: число делится на 12, тогда, когда оно одновременно делится на 3 и на 4.
Например, 408:12, т.к. 4+0+8=12 (12:3) и две последние цифры делятся на 4 (08:4)
Признак делимости на 14: число делится на 14 тогда, когда оно делится на 2 и на 7.
Например, число 45612:14 т. к. оно делится и на 2 и на 7 , значит, оно делится и на 14.
Признак делимости на 15: число делится на 15 тогда, когда оно делится на 3 и на 5.
Например, 1146795:15 т.к. это число делится и на 3 и на 5.
Признаки делимости на 27: число делится на 27 тогда, когда оно делится на 3 и на 9.
Например, 511704:27 т.к. 5+1+1+7+0+4=18, (18:3 и 18:9)
Признаки делимости на 30: число делится на 30 тогда, когда оно заканчивается на 0 и сумма всех цифр делится на 3.
Например, 510:30 т.к. 5+1+0=6 (6:3) и в числе 510 (последняя цифра 0)
Признаки делимости на 60: для того, чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось на 4, на 3, на 5.
Например, 1620:60 т.к. 1+6+2+0=9 (9:3), число 1620 заканчивается 0, т.е. делится на 5 и 1620 : 4 т.к. две последние цифры 20:4
Применение признаков делимости на практике
Работа имеет практическое применение. Ее могут использовать школьники и взрослые при решении реальных ситуаций; учителя, как при проведении уроков по математике, так и на факультативных курсах и дополнительных занятий на повторение.
Данное исследование будет полезным для учащихся при самостоятельной подготовке к выпускным и вступительным экзаменам. А также будет полезно и для учеников, целью которых стали высокие места на городских олимпиадах.
Задача № 1. Можно ли, используя только цифры 3 и 4, записать:
число, которое делиться на 10;
четное число;
число, кратное 5;
нечетное число
Задача № 2
Напишите какое-нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 1.
Напишите наибольшее из таких чисел.
Напишите наименьшее из таких чисел.
Ответ: 987652413; 102347586
Задача № 3
Найдите наибольшее четырехзначное число, все цифры которого различны и которое делится на 2, 5, 9, 11.
Ответ: 8910
Задача № 4
Оля задумала простое трехзначное число, все цифры которого различны. На какую цифру оно может заканчиваться, если его последняя цифра равна сумме первых двух. Приведите примеры таких чисел.
Ответ: только на 7. Есть 4 числа удовлетворяющие условию задачи: 167, 257, 347, 527
Задача № 5
В двух классах вместе 70 учеников. В одном классе 7/17 учеников не явились на занятия, а в другом 2/9 получили отличные отметки по математике. Сколько учеников в каждом классе?
Решение: В первом из этих классов могло быть: 17, 34, 51… - числа, кратные 17. Во втором классе: 9, 18, 27, 36, 45, 54… - числа, кратные 9. Нам нужно выбрать 1 число из первой последовательности, а 2 число из второй так, чтобы они в сумме давали 70. Причем в этих последовательностях только небольшое число членов могут выражать возможное количество детей в классе. Это соображение существенно ограничивает перебор вариантов. Возможным единственным вариантом оказалась пара (34, 36).
Задача № 6
В 9 классе за контрольную работу 1/7 учеников получили пятёрки, 1/3 – четверки, ½ - тройки. Остальные работы оказались неудовлетворительными. Сколько было таких рабо
Решение: Решением задачи должно являться число, кратное числам: 7, 3, 2. Найдем сначала наименьшее из таких чисел. НОК (7, 3, 2) = 42. Можно составить выражение по условию задачи: 42 – (42 : 7 + 42 : 3 + 42 : 2) = 1 – 1 неуспевающий. Математические отношение отношения задачи допускают, что число учеников в классе 84, 126 и т.д. человек. Но из соображений здравого смысла следует, что наиболее приемлемым ответом является число 42.
Ответ: 1 работа.
Заключение:
В результате выполнения данной работы я узнала, что кроме известных мне признаков делимости на 2, 3, 5, 9 и 10 существуют еще и другие признаки делимости натуральных чисел. Полученные знания значительно ускоряет решение многих задач. И я смогу использовать эти знания в своей учебной деятельности, как на уроках математики, так и во внеклассных занятиях. Следует так же отметить, что формулировки некоторых признаков делимости сложные. Может быть, поэтому они не изучаются в школе. Предполагаю и в дальнейшем продолжить работу по изучению признаков делимости натуральных чисел.
Библиографический список:
Энциклопедический словарь юного математика. Савин А.П. Москва «Педагогика» 1989.
Математика. Дополнительные материалы к уроку математики 5-11 классы. Рязановский А.Р., Зайцев Е.А. Москва «Дрофа» 2002.
За страницами учебника математики. Виленкин Н.Я., Депман И.Я. М.: Просвещение, 1989.
Внеклассная работа по математике в 6-8 классах. Москва. «Просвещение» 1984 г. В. А. Гусев, А. И. Орлов, А. Л. Розенталь.
«1001 вопрос и ответ. Большая книга знаний» Москва. «Мир книги» 2004.
Факультативный курс по математике. Никольская И.Л. – Москва. Просвещение 1991.
Олимпиадные задачи по математике и методы их решения. Фарков А. В. - Москва. 2003г.
Интернет ресурсы.
13