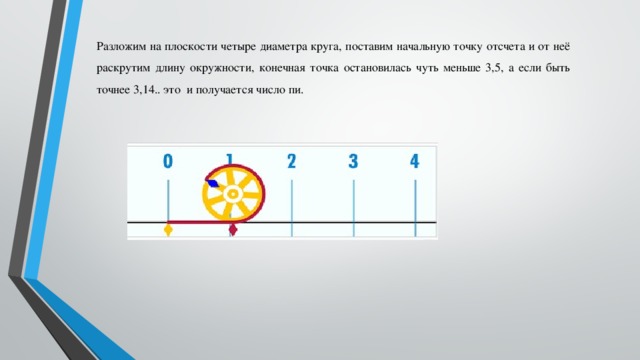
ГОБУ СПО ВО «ВАТ им. В.П. Чкалова»
Исследовательская работа:
«Знакомство с числом π»
Выполнил:
студент группы ТМ-143
Валяев Дмитрий
Проверил:
преподаватель математики
Гетманская С.А.
2014 г
Содержание
| Введение | 3 |
| История числа «пи» | 4 |
| Рекорд запоминания числа | 6 |
| Мистика числа | 8 |
| Забавные факты | 9 |
| Загадка числа: π= 2 или π=4? | 10 |
| Эксперимент по вычислению приближенного значения | 12 |
| День рождения «пи» | 12 |
| Буква π в архитектуре | 13 |
| Число π в школьной жизни | 14 |
| Заключение | 20 |
| Используемая литература | 21 |
Введение
Никакое другое число не является таким загадочным, как "Пи" с его знаменитым никогда не кончающимся числовым рядом. Во многих областях математики и физики ученые используют это число и его законы.
Его можно встретить в теории вероятностей, в решении задач с комплексными числами и прочих неожиданных и далеких от геометрии областях математики. Английский математик Август де Морган назвал как-то "пи" “…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу”. Это таинственное число, связанное с одной из трех классических задач Античности - построение квадрата, площадь которого равна площади заданного круга - влечет за собой шлейф драматических исторических и курьезных занимательных фактов.
Кто разгадал загадку этого числа, к сожалению, не знает никто. Но многие математики пытались приоткрыть завесу тайны…
Определенная часть людей на нашей планете знает, что существует число пи. Почти половина из этого количества может сказать, что оно обозначает и где применяется. И уж совсем немногие могут рассказать, как появилось это загадочное число и почему оно так прочно укоренилось в нашей жизни. В своей исследовательской работе я рассмотрела многие вопросы, касающиеся данного значения, а также где в школьном курсе встречается данное число, чем оно может нам «помочь». В связи с этим считаю свою работу актуальной.
Цель работы- показать важность проблемы вычисления числа Пи, раскрыть необходимость точных вычислений значения Пи на современном этапе, а также показать огромное трудолюбие и работоспособность ученых, занимавшихся этим вопросом на протяжении многих столетий, где в школьной жизни мы применяем данное значение.
Исследовательская работа включает в себя презентацию и текстовую работу.
Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы нам не ошибаться,
Чтоб окружность верно счесть,
Надо только постараться
И запомнить все как есть
Три — четырнадцать —
пятнадцать — девяносто два и
шесть!
С.Бобров
История числа "пи"
Число π (произносится «пи») — математическая константа, выражающая отношение длины окружности к длине её диаметра. Обозначается буквой греческого алфавита «пи».
В священной книге джайнизма (одной из древнейших религий, существовавших в Индии и возникшей в VI в. до н.э.) имеется указание, из которого следует, что число π в то время принимали равным  , что даёт дробь 3,162... Древние греки Евдокс, Гиппократ и другие измерение окружности сводили к построению отрезка, а измерение круга - к построению равновеликого квадрата. Следует заметить, что на протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом.
, что даёт дробь 3,162... Древние греки Евдокс, Гиппократ и другие измерение окружности сводили к построению отрезка, а измерение круга - к построению равновеликого квадрата. Следует заметить, что на протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом.
Архимед в III в. до н.э. обосновал в своей небольшой работе "Измерение круга" три положения:
Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
Отношение любой окружности к её диаметру меньше 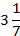 и больше
и больше  .
.
Последнее предложение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. Сначала он удвоил число сторон правильных описанного и вписанного шестиугольников, затем двенадцати угольников и т.д., доведя вычисления до периметров правильного вписанного и описанного многоугольников с 96 сторонами.
По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 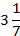 и
и  , а это означает, что π = 3,1419... Истинное значение этого отношения 3,1415922653... В V в. до н.э. китайским математиком Цзу Чунчжи было найдено более точное значение этого числа: 3,1415927...
, а это означает, что π = 3,1419... Истинное значение этого отношения 3,1415922653... В V в. до н.э. китайским математиком Цзу Чунчжи было найдено более точное значение этого числа: 3,1415927...
В первой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил πс 16 десятичными знаками. Ал-Каши произвёл уникальные расчёты, которые были нужны для составления таблицы синусов с шагом в 1'. Эти таблицы сыграли важную роль в астрономии.
Спустя полтора столетия в Европе Ф. Виет нашёл число πтолько с 9 правильными десятичными знаками, сделав 16 удвоений числа сторон многоугольников. Но при этом Ф. Виет первым заметил, что π можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, так как позволило вычислить πс какой угодно точностью. Только через 250 лет после ал-Каши его результат был превзойдён.
Первым ввёл обозначение отношения длины окружности к диаметру современным символом π английский математик У.Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова "periferia", что в переводе означает "окружность". Введённое У.Джонсоном обозначение стало общеупотребительным после опубликования работ Л.Эйлера, который воспользовался введённым символом впервые в 1736 г.
В конце XVIII в. А.М.Лажандр на основе работ И.Г.Ламберта доказал, что число π иррационально. Затем немецкий математик Ф.Линдеман, опираясь на исследования Ш.Эрмита, нашёл строгое доказательство того, что это число не только иррационально, но и трансцендентно, т.е. не может быть корнем алгебраического уравнения. Из последнего следует, что с помощью только циркуля и линейки построить отрезок, равный по длине окружности, н е в о з м о ж н о, а следовательно, не существует решения задачи о квадратуре круга.
Поиски точного выражения пи продолжались и после работ Ф.Виета. В начале XVII в. голландский математик из Кёльна Лудольф ван Цейлен (1540-1610) нашёл 32 правильных знака. С тех пор (год публикации 1615) значение числа π с 32 десятичными знаками получило название числа Лудольфа.
К концу XIX в., после 20 лет упорного труда, англичанин Вильям Шенкс нашёл 707 знаков числа π. Однако в 1945 г. обнаружено с помощью ЭВМ, что Шенкс в своих вычислениях допустил ошибку в 520-м знаке и дальнейшие его вычисления оказались неверными.
После разработки методов дифференциального и интегрального исчисления было найдено много формул, которые содержат число "пи". Некоторые из этих формул позволяют вычислить "пи" приёмами, отличными от метода Архимеда и более рациональными.
Рекорд запоминания числа
Запомнить знаки π человечество пытается уже давно. Но как уложить в память бесконечность? Любимый вопрос мнемонистов-профессионалов. Разработано множество уникальных теорий и приёмов освоения огромного количества информации. Многие из них опробованы на π.
Мировой рекорд, установленный в прошлом столетии в Германии - 40 000 знаков. Российский рекорд значений числа π 1 декабря 2003 года в Челябинске установил Александр Беляев. За полтора часа с небольшими перерывами на школьной доске Александр написал 2500 цифр числа π.
До этого рекордным в России считалось перечислить 2000 знаков, что удалось сделать в 1999 году в Екатеринбурге. По словам Александра Беляева - руководителя центра развития образной памяти, такой эксперимент со своей памятью может провести любой из нас. Важно лишь знать специальные техники запоминания и периодически тренироваться.
Последний рекорд, достигнутый на суперкомпьютерах - это 500 млрд. знаков.
На данный момент известно 12 тысяч 411 триллионов знаков после запятой.
Это результат математических изысканий японского ученого Исумасо Канадае.
Фанаты загадочного числа Пи пытаются заучить как можно больше цифр после запятой.
Рекорд принадлежит колумбийцу Хайме Гарсия. Он умудрился воспроизвести 150 тысяч знаков. На это ему потребовалось три дня.
Математики вычислили уже около пяти триллионов знаков в числе Пи, а мы в своем обиходе используем только три. Однако если вам необходимо использовать более точное значение, есть несколько простых способов его запомнить.
1 способ:
Если вам достаточно знать всего на пару знаков больше, чем обычно, вам поможет фраза: «Что я знаю о кругах». Подсчитав количество букв в каждом слове, вы получите следующую комбинацию цифр: 3,1415.
2 способ:
Если вам нужно знать больше знаков после запятой или же первый способ просто кажется неудобным, вам поможет следующее стихотворение:
Нужно только постараться
И запомнить все как есть.
Три, четырнадцать, пятнадцать,
Девяносто два и шесть!
3 способ:
С помощью другого стихотворения можно запомнить 10 знаков после тройки (3,1415926535):
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
4 способ:
Классический способ запомнить 11 знаков после запятой – выучить следующее двустишие:
Это я знаю и помню прекрасно –
Пи. Многие знаки мне лишни, напрасны.
Количество букв в каждом слове поможет вам получить число 3,14159265358.
5 способ:
Если же вам нужна еще более высокая точность, то вам поможет продолжение одного из мнемонических стихотворений:
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим -
Это будет пять, три, пять,
Восемь, девять, восемь.
В итоге вы с легкостью запомните число 3,1415926535898, содержащее целых 13 знаков после запятой.
Мистика числа
Считается, что каждому, кто попытается разгадать число Пи, грозит смерть. Несколько веков подряд его боялись и считали проклятым.
В 1829 году норвежский математик Нильс Абель заявил, что число ПИ разумно и даже умеет разговаривать. Ученый утверждал, что в беседах число просит остаться неразгаданным. Но Абель решил, во что бы то ни стало раскрыть его тайну. Через 2 месяца он умер.
Профессор Оксфордского университета Годфри Харди и вовсе заявил, что он женат на числе Пи - царице этого мира. Со своей возлюбленной ученый беседовал каждый день, когда пытался вычислить все новые цифры после запятой.
Хотя π является, безусловно, интересным числом, его мистичность обусловлена, по-видимому, тем, что «пи» - одно из самых древних математических понятий, которое мы в состоянии проследить в истории. Некоторые ученые приписывают честь открытия этого числа Архимеду, другие утверждают, что оно было известно гораздо раньше. Одним из самых интересных свойств числа «пи» является возможность рассчитать с его помощью длину окружности большой сферы. Такой расчет можно провести с очень высокой точностью благодаря бесконечному числу цифр после запятой в десятичной форме этого числа.
«Пи» - одно из тех необычных чисел, к которым относятся омега, дельта и другие и которые, как пишет сэр Мартин Риз, вне всякого сомнения, будут теми же и для пришельца из другой вселенной. Число «пи» представляет отношение, которое будет тем же самым независимо от того, в какой вселенной вы пребываете, и независимо от объекта измерения. «Пи» - это «пи», вне зависимости от того, куда вы направляетесь.
Такой тип константы буквально вплетен в ткань нашей Вселенной и, возможно, многих других вселенных.
«Пи» обладает репутацией несколько «противоречивого» числа, поддающегося нескольким интерпретациям. Согласно Майклу Хэйесу, автору книги «Герметический код ДНК: сакральные принципы организации Вселенной», число π ассоциируется с музыкой, гармонией и с самой ДНК. При желании можно найти любой номер телефона или даже код к кредитной карточке.
Посмотрим на начало этого бесконечного числа: π = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Забавные факты
В штате Индиана (США) в 1897 был выпущен билль, законодательно устанавливающий значение числа πравным 3,2. Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью, присутствовавшем во время рассмотрения принятия данного закона.
Выход нового диска Кейт Буш "Aerial" заставил сердца математиков забиться сильнее. В песне, которую певица так и назвала – "Пи", прозвучали 124 числа из знаменитого числового ряда 3,141…
Пи заворожило не только Кейт Буш. С давних времен загадка этого числа не давала покоя многим ученым, особенно математикам - именно в этой области многие разделы науки не могут обойтись без законов этого таинственного числа.
Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему…целый дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи. Сейчас волшебный дворец находится под охраной ЮНЕСКО.
Как пишет "Die Welt", существует и Пи-клуб, члены которого, являясь фанатами загадочного математического феномена, собирают все новые сведения о Пи и пытаются разгадать его тайну. Чтобы вступить в него, для начала надо вызубрить наизусть как можно большее количество чисел Пи после запятой. Пока рекорд принадлежит японцу Акира Харагучи, запомнившему 83 431 цифру.
А вот певицу Кейт Буш, несмотря на то, что она увековечила в своей песне знаменитое число, в клуб фанатов Пи не примут. В ее песне неправильно названо 25-е число последовательности, да и потом исчезли куда-то целых 22 числа. Так что ей предстоят упорные тренировки.
Существует даже аромат, который назван в честь загадочного числа «пи» - основы многих вычислений, открытий и инноваций. Этот аромат был создан под руководством Александра МакКуина (Alexander McQueen) - коренного англичанина в Париже, поэтому он не мог не получиться неординарным и уникальным, ведь в нем смешалось два мира: английское спокойствие и французская любовь к праздникам. Флакон аромата - отдельное произведение искусства. Он был создан знаменитым дизайнером Сержем Мансо (Serge Mansau) и представляет собой прозрачную пирамиду с вытесненными геометрическими узорами.
Даже на улицах некоторых городов можно встретить число π в виде названия улицы или украшения здания.
Вполне очевидно, что о роли числа π знают и представители высокоразвитых внеземных цивилизаций. Это может подтвердить случай, произошедший в 2009 году, когда примерно в 130 километрах от Лондона на полях в графстве Уилтшир (Wiltshire), около местечка Barbury Castle появились загадочные знаки.
Рядом с этим полем сохранились остатки построек древней доримской эпохи. На поле появился рисунок из полегших колосьев. Астрофизик из США Михаэль Рид (Michael Reed) смог прочитать этот узор и увидел, что в нем зашифровано число «Пи» с точностью до 9 знаков после запятой.
Результат этой расшифровки просто очевиден и понятен и доступен даже людям, далеким от математики и геометрии.
Михаэль Рид вспоминает: «Сначала это показалось мне забавным. Я продолжил. За дугой из четырех секторов - после очередной ступеньки - оказалась дуга в один сектор. Затем в пять, в девять, в два, и так далее. В результате получилось 3.141592654 - это число "Пи" с точностью до девятого знака! И кому понадобилось об этом сообщить..?»
Выходит, что инопланетяне дают нам знать о возможностях загадочного числа «Пи», лежащего в основе мироздания. Значит, даже они считают это число основой всей жизни во Вселенной.
В Лейпциге было обнаружено таинственное яйцо с нанесенными на нем 2345 цифрами числа пи.
Автомобиль «Мазда π» был обнаружен в американском штате Массачусетс.
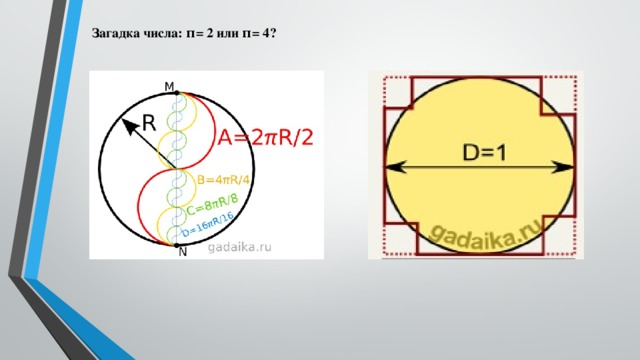
Загадка числа: π= 2 или π=4?
Докажем, что π=2.
Дано: окружность радиуса R. Кривая А (на рисунке красная) построена из двух полуокружностей радиуса R/2. Следовательно, длина кривой А равна π*R. Кривая B построена из четырёх полуокружностей радиуса R/4, её длина также равна π *R. Аналогично, кривая C построена из восьми полуокружностей радиуса R/8 и длина её так же составляет π *R. Продолжая построение, получим последовательность кривых, составленных из полуокружностей радиуса, стремящегося к нулю, длина всех этих кривых равна π *R.
Очевидно, что кривые, с увеличением числа составляющих полуокружностей и с уменьшением их радиуса, стремятся к отрезку MN, длина которого равна 2R. Таким образом, получаем:
π *R = 2R, следовательно, π = 2
А теперь - вопрос: доказано, что число Пи равно двум. Почему же повсеместно используется более длинное и неудобное значение 3.1415...?
Ответ: С уменьшением радиуса полуокружностей, составляющих кривую, она приближается к отрезку-диаметру MN, однако форма полуокружностей не меняется. Сколь "мелкими" они бы ни становились, их длина всё равно будет равняться π*R.
Поэтому, как это ни печально, число π не равно двум. А как было бы удобно, если бы это было правдой!
Так же есть загадка, что число π равно 4.
Рассмотрим пример. Начертим окружность с диаметром, равным единице:
Теперь опишем квадрат вокруг этой окружности. Периметр этого квадрата будет равен четырём, ведь каждая сторона равна единице.
Теперь "отрежем" углы у квадрата, чтобы получившаяся фигура более точно повторяла окружность. Отрезать будем прямоугольные кусочки, поэтому периметр фигуры, которая раньше была квадратом, не изменится.
Повторяем "отрезание", чтобы оставшаяся от квадрата часть была похожа на круг. Кое-где можно не отрезать, а наоборот, "добавлять" прямоугольные кусочки, чтобы максимально приблизить фигуру к окружности. Периметр при этом, опять же, не меняется.
Проделав это бесконечное число раз (с каждым разом фигура приближается к окружности), получим точный контур окружности. А ведь фигура, которую мы "превратили" в круг, имеет всё тот же периметр, равный четырём! Этот периметр теперь - длина окружности, получившейся из квадрата. Диаметр этой окружности равен единице. Найдём теперь число π из определения:
π = 4 / D = 4.
Итак, доказано: число Пи равно четырём.
«Правильное» решение: данное «доказательство» представляет собой софизм. Кажется, что фигура, которая получается из квадрата, и в самом деле будет в точности повторять круг: ведь все отрезки, из которых состоит фигура, будут находиться сколь угодно близко к окружности.
Несмотря на это, фигура кругом никогда не станет, потому что сколь малыми бы ни были её элементы, они представляют собой "угловатую" ломаную линию, периметр которой не меняется.
Далее рассмотрим «правильное» вычисление значения π.
Эксперимент по вычислению приближенного значения отношения длины окружности к диаметру.
Возьмём 4 любые предметов: стакан, кружку, баночку с кремом, шоколадную медаль.
Измерим диаметр каждого предмета и длину окружности с помощью нити и линейки, имеющей цену деления 1 мм и соответственно погрешность 0,5 мм.
Вычислим для каждого случая значение числа π, округлив результат до тысячных.
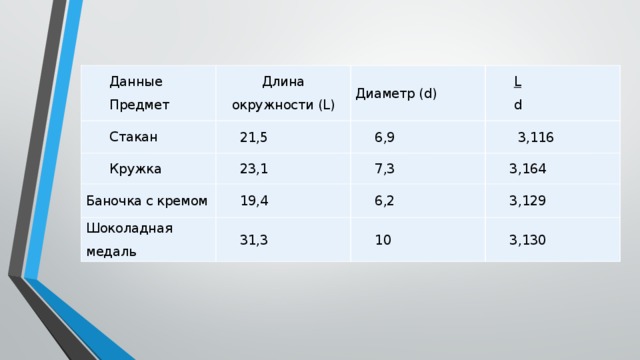
Составим таблицу по найденным данным :
| Данные Предмет | Длина окружности (L) | Диаметр (d) | L d |
| Стакан | 21,5 | 6,9 | 3,116 |
| Кружка | 23,1 | 7,3 | 3,164 |
| Баночка с кремом | 19,4 | 6,2 | 3,129 |
| Шоколадная медаль | 31,3 | 10 | 3,130 |
Вывод: отношение длины окружности к диаметру приближается к 3,14. Точность вычисления числа «Пи» таким способом невелика.
День рождения «пи»
У числа π есть день рождение. Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта (в американском написании 3.14) ровно в 01:59 дата и время совпадут с первыми разрядами числа π= 3,14159.
14 марта 1879 года также родился создатель теории относительности Альберт Эйнштейн, что делает этот день еще более привлекательным для всех любителей математики.
Кроме того, математики отмечают и день приближенного значения π, который приходится на 22 июля (22/7 в европейском формате записи даты).
"В это время читают хвалебные речи в честь числа Пи и его роли в жизни человечества, рисуют антиутопические картины мира без Пи, едят пироги с изображением греческой буквы Пи или с первыми цифрами самого числа, решают математические головоломки и загадки, а также водят хороводы", – пишет Википедия.
На День Рождения числа Пи принято печь круглый пирог, с узором внутри пирога в виде значка .
Также в этот день заведено читать дифирамбы в честь числа «Пи», активисты подготавливают доклады о его роли в жизни всего человечества, решают математические задачи и головоломки, рисуют неидеальные картины мира без π.
Буква π в архитектуре
Египетские пирамиды. Они уже в древности считались одним из семи «чудес света». Само их существование, тайна возникновения и предназначения в течение тысячелетий будоражили воображение лучших человеческих умов. Вызывает любопытство и восхищение и становится интеллектуальным вызовом человечеству, демонстрацией его бессилия в раскрытии этих тайн. Пирамиды до сего времени — тайны втройне. Раскрытию этих тайн многие ученые посвятили всю свою жизнь. Однако на протяжении тысячелетий, начиная с Геродота, посетившего Египет еще до рубежа новой эры, и до сего времени, эти тайны не поддаются расшифровке.
Главные вопросы, всегда волновавшие исследователей пирамид Египта, можно свести к четырем позициям: кто, когда, как, и, главное, зачем построил эти величественные сооружения? Но мы не будем сейчас рассматривать эти вопросы, а коснемся только математических знаний, воплощенных в архитектуре пирамид.
Здесь тоже не обошлось без этого числа. Если принять диаметр за единицу, то длина окружности — это и есть число «пи» и равняется 3,1415926... Официально считается, что первым, кто предложил математический способ вычисления, был Архимед. Но как утверждают современные ученые, впервые число «пи» стало применяться в Египте около 1700 года до н. э. Упоминание об этой закономерности можно найти даже в папирусе Ахмеса, а это более тысячи лет до Архимеда, что говорит о том, что египетские математики не только знали, но и активно пользовались этим числом в инженерных расчетах. Но пирамиды предположительно были построены за тысячу лет до этих времен. Возможно, египтяне знали об этой величине задолго до указанной даты и все дело в том, что папирус Ахмеса — это один из немногих дошедших до нашего времени древних документов.
Стоит представить себе изумление ученых 19 века, которые впервые обнаружили, что пропорции пирамиды Хеопса тесно связаны с числом «пи». В частности, если разделить длину периметра основания этой пирамиды на ее удвоенную высоту, появляются знакомые каждому школьнику цифры. Проведенные советским исследователем Н. А. Васютинским исследования пропорций пирамиды Хеопса выявили некоторые погрешности между известным числом «пи» и соотношением высоты и размера основания этого древнего сооружения. Погрешность составила всего 15 десятитысячных долей процента. Продолжив свои исследования, Васютинский выяснил, что увеличение высоты пирамиды всего на один египетский «локоть» или уменьшение ее на ту же величину привело бы к появлению величины 3.135 и 3.154 соответственно, т.е. говорить о точности числа «пи» уже не приходилось бы. Но этого не произошло, т.е. древнеегипетские проектировщики использовали в своих расчетах именно число «Пи», а теми, кем была построена усыпальница Хеопса, были с поразительной точностью выдержаны запланированные пропорции. Каким образом им удалось это сделать, похоже, так и останется неразгаданной загадкой!
Пирамиды строго ориентированы по сторонам света, все их размеры связаны со значением числа Пи с точностью до нескольких знаков после запятой.
При изучении пирамид в Египте оказалось, что периметр пирамиды Хеопса, разделенный на удвоенную высоту, дает точное значение числа "пи" с точностью до 0,01
Это легко проверить:
сторона основания - 230,3 м, периметр - 203,3x4 = 921,2 м.
Высота пирамиды - 146,6 м, удвоенная - 293,2 м.
Делим первую величину на вторую и получаем: 921,2/293,2 = 3,14 (число "пи").
Так же числоπ использовалось при строительстве знаменитой Вавилонской башни. Однако недостаточно точное исчисление значения числа “ПИ” привело к краху всего проекта.
Есть предположения, эта математическая константа лежала в основе строительства легендарного Храма царя Соломона. В 7-й главе 1-й книги Шофтим (Судей) приводится описание медного моря, сделанного мастером Хирамом из Цура по приказу царя Соломона. «И сделал он море литое десять локтей от края до края круглое вокруг, и пять локтей высота его и линия в тридцать локтей опоясывала его вокруг» (стих 23). Поскольку диаметр сосуда был 10 локтей, а периметр 30, то следовательно их отношение равно трём. Довольно грубое приближение числа π=3.1415…!
Еще один интересный факт, уже из более близкой к нам истории: германский король Фридрих II был настолько очарован этим числом, что посвятил ему дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи.
Число π в школьном курсе
В современной математике число π — это не только отношение длины окружности к диаметру, оно входит в большое число различных формул, в том числе и в формулы неевклидовой геометрии. Входит она и в замечательную формулу Л. Эйлера, которая устанавливает связь числа Пи числа е. Эта и другие взаимосвязи позволили математикам ещё глубже выяснить природу числа. Число Пи одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки:
в уравнениях гравитационного поля Эйнштейна;
в уравнениях, связанных с образованием радуги;
в уравнениях описывающих распространение зыби при падении дождевой капли в воду;
в уравнении нормального распределения Гаусса;
в уравнении движения маятника, во многих геометрических задачах, в задачах связанных с волнами;
в задачах навигации и т.д.
В своей работе я рассмотрела при изучении каких тем в школьном курсе можно встретить число π и чем оно может помочь.
Первый раз мы встречаем букву π в учебнике Н.Я. Виленкин, В.И. Жохов и др. Математика 6 класс.
В учебнике приводится такое объяснение: Возьмем круглый стакан, поставим на лист бумаги и обведем карандашом. На бумаге получилась окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближено равна длине нарисованной окружности.
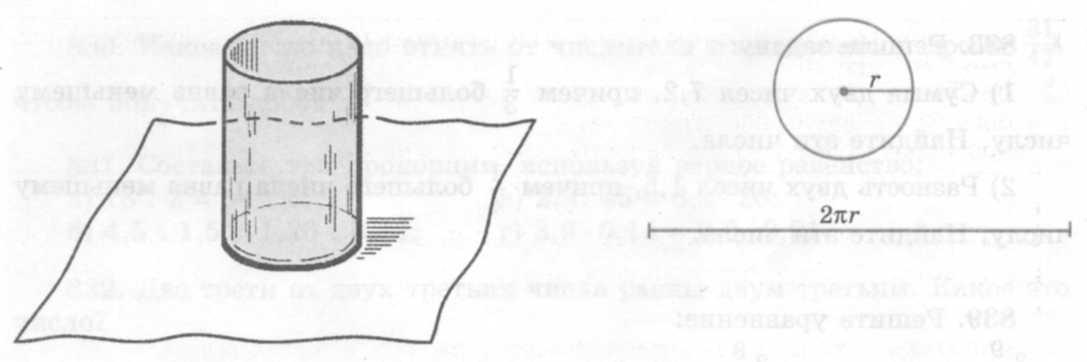
Также приводится формула для нахождения длины окружности и площади круга.
Н а рисунке изображены круг и два квадрата ABCD и EFKM. Радиус круга равен r, поэтому длина стороны квадрата ABCD равна 2r, а его площадь 4r2.
а рисунке изображены круг и два квадрата ABCD и EFKM. Радиус круга равен r, поэтому длина стороны квадрата ABCD равна 2r, а его площадь 4r2.
Площадь треугольника EOF вдвое меньше площади квадрата AEOF, поэтому площадь EFKM вдвое меньше площади квадрата ABCD, т. е. равна 2r2. Площадь круга S больше площади квадрата EFKM, но меньше площади квадрата ABCD:
2r2 S r2.
Примерно площадь круга равна 3r2. Можно доказать, что
S = πr2.
На применение формул даются такие задания: Выполните необходимые измерения и найдите длину половины окружности, изображенной на рисунке.
П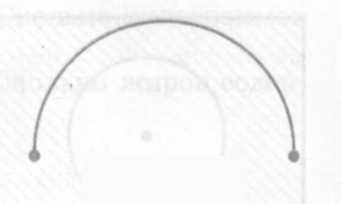 ри решении задач такого типа, необходимо линейкой измерить расстояние от точки до точки, разделить на 2. Применить формулу длины окружности, а так как на рисунке приведена только половина окружности, то разделить на 2.
ри решении задач такого типа, необходимо линейкой измерить расстояние от точки до точки, разделить на 2. Применить формулу длины окружности, а так как на рисунке приведена только половина окружности, то разделить на 2.
Задания такого типа не вызывают затруднений у учащихся, так как уровень сложности незначительный, но развивают аналитическое мышление.
Позже в 9 классе по геометрии мы так же встречаем букву π, когда проходим теорему об отношении длины окружности к ее диаметру: отношение длины окружности к ее диаметру не зависит от окружности, т.е. одно и то же для любых окружностей.
Докажем это.
Доказательство.
Возьмем две произвольные окружности. Пусть R1 и R2 — их радиусы, а l1 и l2 — их длины.
Д опустим, что утверждение теоремы не-
опустим, что утверждение теоремы не-
верно и � � , например:
� , например:
�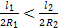 � (1)
� (1)
Впишем в наши окружности правильные выпуклые многоугольники с большим числом сторон п. Если п очень велико, то длины наших окружностей будут очень мало отличаться от периметров р1 и р2 вписанных многоугольников. Поэтому неравенство (1) не нарушится, если в нем заменить l1 на p1, а l2 на р2:
�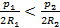 � (2)
� (2)
Но, как мы знаем, периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей:

Отсюда �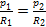 �
�
А это противоречит неравенству (2).
Теорема доказана.
Здесь же и вводится понятие «отношение длины окружности к диаметру» через букву π.
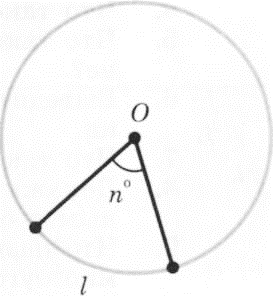 Далее мы встречаемся с π при изучении радианной меры угла.
Далее мы встречаемся с π при изучении радианной меры угла.
Найдем длину дуги окружности, отвечающей центральному углу в п°.
Развернутому углу соответствует длина полуокружности πR. Следовательно, углу в 1° соответствует дуга длины � �, а углу в п° соответствует дуга длины �
�, а углу в п° соответствует дуга длины � �.
�.
Р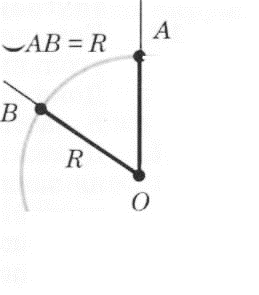 адианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности. Из формулы для длины дуги окружности следует, что
адианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности. Из формулы для длины дуги окружности следует, что
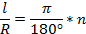
т. е. радианная мера угла получается из градусной
умножением на � �. В частности, радианная мера угла 180° равна π, радианная мера прямого угла равна �
�. В частности, радианная мера угла 180° равна π, радианная мера прямого угла равна � �
�
Единицей радианной меры углов является радиан. Угол в один радиан — это угол, у которого длина дуги равна радиусу. Градусная мера угла в один радиан равна � �.
�.
В практической части приводится ряд задач, решение которых не обходится без π.
В теме «Площадь круга и его частей» буква π просто незаменима.
�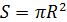 � –площадь круга
� –площадь круга
�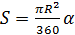 � –площадь кругового сектора
� –площадь кругового сектора
� � –площадь сегмента
� –площадь сегмента
Рассмотрим такой пример: Найдите отношение площади круга к площади вписанного в него квадрата.
Р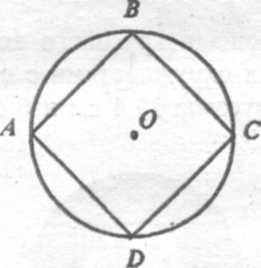 ешение: Пусть ABCD — квадрат, вписанный в круг. Тогда
ешение: Пусть ABCD — квадрат, вписанный в круг. Тогда 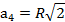 ,
, 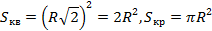 , следовательно: �
, следовательно: �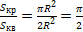 �
�
Геометрия 11 класса позволяет встречаться с данной буквой довольно часто при изучении тел вращения: конус, цилиндр, шар. Достаточно представить себе конус, цилиндр или шар и в каждом модно найти хотя бы один круг (в шаре их –бесконечность). Приведем такой пример.
Шар, радиус которого 41 дм, пересечен плоскостью на расстоянии 9дм от центра. Найдите площадь сечения.
Р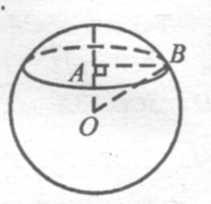 ешение: В прямоугольном АОВ по теореме Пифагора:
ешение: В прямоугольном АОВ по теореме Пифагора:
АВ = �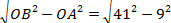 � =40 (дм).
� =40 (дм).
Тогда площадь сечения S = π-АВ2 = π402 = 1600π (дм2) = 16 π (м2).
Ответ: 16π м2.
Число π встречается и в формулах вычисления объемов и площади боковой поверхности тел вращения.
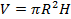 –объем цилиндра
–объем цилиндра
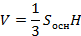 – объем конуса
– объем конуса
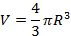 – объем шара
– объем шара
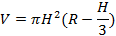 – объем шарового сегмента
– объем шарового сегмента
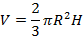 – объем шарового сектора
– объем шарового сектора
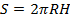 – боковая поверхность цилиндра
– боковая поверхность цилиндра
 – боковая поверхность конуса
– боковая поверхность конуса
 – боковая поверхность шара
– боковая поверхность шара
Рассмотрим пример, где при расчете обязательно понадобится буква π .
Задача: Куча щебня имеет коническую форму, радиус основания которой 2 м, а образующая 2,5 м. Найдите объем кучи щебня.
Р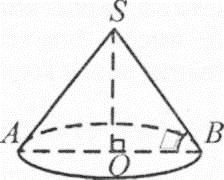 ешение: В S АО по теореме Пифагора получаем:
ешение: В S АО по теореме Пифагора получаем:
�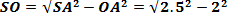 �=1,5 (м)
�=1,5 (м)
Тогда объем кучи:
�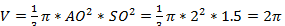 �(м3) �
�(м3) � �.
�.
Ответ: 6,3 м3.
Задача: Из деревянного цилиндра, высота которого равна диаметру основания, выточен наибольший шар. Сколько процентов материала сточено?
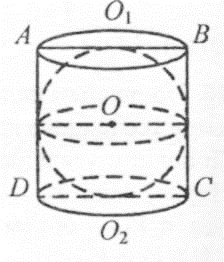 Решение: Радиус шара равен радиусу цилиндра и половине высоте цилиндра. Тогда, если R — радиус цилиндра, то объем шара
Решение: Радиус шара равен радиусу цилиндра и половине высоте цилиндра. Тогда, если R — радиус цилиндра, то объем шара 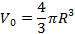 ��, а объем цилиндра �
��, а объем цилиндра �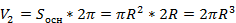 �.
�.
Тогда объем сточенного материала � �
�
А процентное соотношение:

Также в школьном курсе можно встретить букву π в физике. Приведем ряд формул, где встречается буква π:
 – циклическая или круговая частота
– циклическая или круговая частота
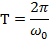 – период колебаний
– период колебаний
 –фаза колебаний
–фаза колебаний
 – третий обобщенный закон Кеплера
– третий обобщенный закон Кеплера
 –критическое значение плотности вещества
–критическое значение плотности вещества
Таким образом, можно сделать вывод, что число π довольно часто встречается в школьном курсе.
Заключение
Число π появляется в формулах, используемых во многих сферах. Физика, электротехника, электроника, теория вероятностей, строительство и навигация - это лишь некоторые из них. И кажется, что подобно тому как нет конца знакам числа π, так нет конца и возможностям практического применения этого полезного, неуловимого числа π.
В современной математике число пи - это не только отношение длины окружности к диаметру, оно входит в большое число различных формул.
Эта и другие взаимозависимости позволили математикам ещё глубже выяснить природу числа пи.
В ходе проведения практического исследования я пришла к следующим выводам: полученное на практике отношение длины окружности к её диаметру приближается к 3,14. Точность вычисления числа «Пи» таким способом невелика: только в одном случае из 5 найденное значение константы содержит верную цифру в разряде сотых, в остальных случаях достигнута точность только в разряде десятых.
В своей работе я хотела показать применение числа при расчетах в школьном курсе при изучении математики и физики и думаю, что достигла поставленной цели.
Используемая литература:
1. "Занимательная арифметика", Я.И.Перельман
2. "Путешествие в историю математики", А.А.Свечников, изд. "Педагогика-Пресс"
3. Еженедельник "Древо познания", изд. "МС ИСТ ЛИМИТЕД",
4. "Старинные занимательные задачи", С.Н.Олехник, Ю.В.Нестеренко, М.К.Потапов, изд. "Вита-Пресс".
5. "Окно в удивительный мир информатики", М.Г.Коляда, изд. "Сталкер".
6. "Устный счет и память", Д.Р.Гончар, А.Р.Лурия, В.В.Аткинсон, изд. "Сталкер"
7. Вездесущее число «пи». Жуков А.В. М.:
8. Физика. Г.Я. Мякшев, Б.Б. Буховцев. Москва. «Просвещение»
9. Геометрия. А.Н. Погорелов. Москва. «Просвещение»
Ссылки
http://crow.academy.ru/dm/materials_/pi/history.htm
http://hab.kp.ru/daily/24123/344634/
http://gadaika.ru/geometry/
4

 а рисунке изображены круг и два квадрата
а рисунке изображены круг и два квадрата  ри решении задач такого типа, необходимо линейкой измерить расстояние от точки до точки, разделить на 2. Применить формулу длины окружности, а так как на рисунке приведена только половина окружности, то разделить на 2.
ри решении задач такого типа, необходимо линейкой измерить расстояние от точки до точки, разделить на 2. Применить формулу длины окружности, а так как на рисунке приведена только половина окружности, то разделить на 2. опустим, что утверждение теоремы не-
опустим, что утверждение теоремы не-
 адианной мерой
адианной мерой ешение: Пусть
ешение: Пусть  ешение: В прямоугольном
ешение: В прямоугольном  ешение: В
ешение: В