| № п/п | Тема урока | Тип урока | Элементы содержания образования | Требования к уровню подготовки
| Формы диагностики и контроля | Домашнее задание (*повышенный уровень) | Дата проведения |
| План | Факт |
| Базовый уровень | Повышенный уровень |
| 1 | 2 | 3 | 4 | 5 | 5 | 6 | 9 | 10 | 11 |
| 1 | Повторение. Свойства степени
с натуральным показателем | Частично-поисковый
| Свойства степени с натуральным показателем, действия со степенями одинакового показателя | Упрощение сложных числовых и алгебраических выражений, используя свойства степени | Знать основные
свойства степени
с натуральным показателем. Уметь применять свойства при решении задач, отделить основную информацию от второстепенной | Взаимопроверка в парах; работа с опорным материалом | Повторить формулы степеней с одинаковыми основаниями.
|
|
|
| 2 | Формулы
сокращенного умножения | Проблемное изложение | Квадрат суммы, квадрат разности, разность квадратов, разность кубов, сумма кубов, разложение на множители по формулам сокращенного умножения | Применение формул сокращённого умножения для упрощения выражений, решения уравнений и неравенств; | Уметь выполнять преобразования многочленов, применяя формулы сокращенного умножения: квадрат суммы и разности, разность квадратов, куб суммы и разности, сумма и разность кубов | Взаимопроверка в парах;
тренировочные упражнения | повторить формулы сокращенного умножения.
|
|
|
| 3 | Функци у=kx + m,
y = x2 и ее график | Комбинированный | Функци у=kx + m,
y = x2, график функций, графическое решение уравнения | Алгоритм графического решения уравнений; решение уравнения графическим способом. | Уметь описывать геометрические свойства прямой и параболы, находить наибольшее и наименьшее значения функций у=kx + m и
y = x2 на заданном отрезке, точки пересечения параболы
с графиком линейной функции | Индивидуальный опрос; выполнение упражнений по образцу | Повторить свойства функций.
|
|
|
| 4 | Повторение. Действия с одночленами и многочленами
| Обобщение и систематизация знаний | Понятия одночлена и многочлена, действия с одночленами и многочленами, разложение многочлена на множители | Разложение многочлена с помощью комбинации нескольких способов, деление многочленов. | Уметь: умножать, делить, складывать и вычитать одночлены и многочлены, возводить одночлен и многочлен в степень; Знать способы разложения многочлена на множители
| Индивидуальное решение контрольных заданий | Дифференцированные задания по карточкам |
|
|
| 5 | Алгебраические дроби. Основные
понятия | Комбинированный | Алгебраическая дробь, числитель дроби, знаменатель дроби, область допустимых значений | Уметь находить рациональным способом значение алгебраической дроби, обосновывать своё решение, устанавливать, при каких значениях переменной не имеет смысла алгебраическая дробь | Иметь представление о числителе, знаменателе алгебраической дроби, значении алгебраической дроби и о значении переменной, при которой алгебраическая дробь не имеет смысла | Работа с конспектом, с книгой и наглядными пособиями по группам | §1, № 1.5(б,г), 1.10(а,б) |
|
|
| 6 | Основное свойство алгебраической дроби | Комбинированный | Основное свойство алгебраической дроби, сокращение дробей, приведение алгебраических дробей к общему знаменателю | Умение преобразовывать пары алгебраических дробей к дроби с одинаковыми знаменателями; раскладывать числитель и знаменатель дроби на простые множители несколькими способами | Иметь представление об основном свойстве алгебраической дроби, о действиях: сокращение дробей, приведение дроби к общему знаменателю.
| Составление опорного конспекта, решение задач | §2, № 2.3(б, г), 2.12, 2.188. |
|
|
| 7 | Основное свойство алгебраической дроби | Поисковый
| Умение преобразовывать тройки алгебраических дробей к дроби с одинаковыми знаменателями; раскладывать числитель и знаменатель дроби на простые множители несколькими способами | Уметь: – применять
основное свойство дроби при преобразовании алгебраических дробей
и их сокращении; – находить значение дроби при заданном значении переменной | Практикум; решение качественных задач | §2, № 2.22(а,г), 2.31, 2.35(б,в)8. |
|
|
| 8 | Сложение
и вычитание алгебраических дробей
с одинаковыми знаменателями | Комбинированный
|
Алгебраическая дробь, алгоритм
сложения
(вычитания) алгебраических дробей
с одинаковыми знаменателями | Уумение доказывать, что дробное выражение при всех допустимых значениях переменной принимает только положительные или отрицательные значения | Иметь представление о сложении
и вычитании дробей с одинаковыми знаменателями. Уметь использовать для решения познавательных задач справочную литературу | Работа с опорными конспектами, раздаточным материалом | §3, № 3.5, 3.7, 3.11(а,в). |
|
|
| 9 | Сложение
и вычитание алгебраических дробей
с одинаковыми знаменателями | Учебный практикум
| Умение находить все натуральные значения переменной, при которых заданная дробь является натуральным числом; излагать информацию, интерпретируя факты, разъясняя значение и смысл теории; развернуто обосновывать суждения | Знать алгоритм сложения и вычитания дробей с одинаковыми знаменателями. Уметь: – складывать и вычитать дроби с одинаковыми знаменателями; – находить общий знаменатель нескольких дробей | Практикум, индивидуальный опрос,
работа с наглядными
пособиями | §3, № 3.16, 3.19(б,г), 3.20(б,г). |
|
|
| 10 | Сложение
и вычитание алгебраических дробей
с разными знаменателями | Комбинированный
| Упрощение выражений, сложение и вычитание алгебраических дробей с разными знаменателями, наименьший общий знаменатель | Знание правила приведения алгебраических дробей к общему знаменателю. Умение упрощать выражения наиболее рациональным способом; развернуто обосновывать суждения | Иметь представление о наименьшем общем знаменателе, о дополнительном множителе,
о выполнении действия сложения и вычитания дробей с разными знаменателями | Работа с конспектом, с книгой и наглядными пособиями по группам | §4, № 4.4, 4.8, 4.13(б). |
|
|
| 11 | Сложение
и вычитание алгебраических дробей
с разными знаменателями | Поисковый
| Правило приведения алгебраических дробей к общему знаменателю, дополнительный множитель, допустимые значения переменных | Умение упрощать выражения, применяя формулы сокращенного умножения, доказывать тождества; | Знать алгоритм сложения и вычитания дробей с разными знаменателями. Уметь: – находить общий знаменатель нескольких дробей; – составить набор карточек с заданиями | Проблемные задания; взаимопроверка в парах; решение упражнения | §4, № 4.16, 4.19(а,б), 4.28(б,г)8. |
|
|
| 12 | Сложение
и вычитание алгебраических дробей
с разными знаменателями | Учебный практикум
| Умение упрощать выражения, применяя формулы сокращенного умножения, доказывать тождества; | Знать алгоритм сложения и вычитания дробей с разными знаменателями. Уметь: – находить общий знаменатель нескольких дробей; – добывать информацию по заданной теме в источниках различного типа | Фронтальный опрос, выборочный диктант, решение качественных задач | §4, № 4.37(б), 4.39(а), 4.518. |
|
|
| 13 | Контрольная работа №1по теме «Сложение и вычитание алгебраических дробей» | Контроль, оценка
знаний |
|
| Знать алгоритм сложения и вычитания дробей с одинаковыми и разными знаменателями. Уметь: – находить общий знаменатель нескольких дробей | Индивидуальное решение контрольных заданий |
|
|
|
| 14 | Анализ контрольной работы. Умножение
и деление алгебраических дробей. | Поисковый
|
Умножение
и деление алгебраических дробей, возведение алгебраических дробей в степень, преобразование выражений, содержащих алгебраические дроби | Умение упрощать выражения наиболее рациональным способом; развернуто обосновывать суждения | Иметь представление об умножении и делении алгебраических дробей, возведении их в степень. Уметь самостоятельно искать
и отбирать необходимую для решения учебных задач информацию | Проблемные задания, фронтальный опрос, упражнения | §5, № 5.2, 5.6, 5.12. |
|
|
| 15 | Возведение алгебраической дроби в степень | Комбинированный
| Умение упрощать выражения, применяя формулы сокращенного умножения, доказывать тождества; | Уметь: – пользоваться
алгоритмами умножения и деления дробей, возведения дроби в степень, упрощая выражения; – развернуто обосновывать суждения | Практикум, фронтальный опрос, упражнения | §5, № 5.14, 5.24, 5.348. |
|
|
| 16 | Преобразование рациональных выражений
| Проблемный | Умение выполнять преобразования рациональных выражений, используя все действия с алгебраическими дробями. Осуществление проверки выводов, положений, закономерностей, теорем | Иметь представление о преобразовании рациональных выражений, используя все действия с алгебраическими дробями. Уметь найти
и устранить причины возникших трудностей | Фронтальный опрос; работа
с демонстрационным материалом | §6, № 6.2(б,в), 6.8, 6.5(г). |
|
|
| 17 | Преобразование рациональных выражений | Поисковый | Выполнение преобразования рациональных выражений, используя все действия с алгебраическими дробями. Умение решать рациональные уравнения; развернуто обосновывать суждения | Знать, как преобразовывают рациональные выражения, используя все действия с алгебраическими дробями. Уметь формировать вопросы, задачи, создавать проблемную ситуацию | Построение алгоритма действия, решение упражнений | §6, № 6.11(б), 6.10(а). |
|
|
| 18 | Преобразование рациональных выражений | Комбинированный
| Умение доказывать тождества, решать рациональные уравнения, задачи, выделяя три этапа математического моделирования. Использование для решения познавательных задач справочной литературы | Уметь: – преобразовывать рациональные выражения, используя все действия с алгебраическими дробями; – участвовать
в диалоге, понимать точку зрения собеседника, признавать право на иное мнение | Работа
с опорными конспектами, раздаточным материалом | §6, № 6.15, 6.18. |
|
|
| 19 | Первые представления о рациональных уравнениях | Комбинированный |
Рациональное уравнение, способ освобождения от знаменателей, составление математической модели | Умение решать рациональные уравнения, применяя формулы сокращенного умножения при их упрощении; | Иметь представление о рациональных уравнениях, об освобождении от знаменателя при решении уравнений. Уметь определять понятия, приводить доказательства | Фронтальный опрос; работа
с демонстрационным материалом | §7, № 7.7, 7.13, 7.248. |
|
|
| 20 | Первые представления о рациональных уравнениях | Учебный практикум | Умение составлять и решать задачи, выделяя три этапа математического моделирования; | Иметь представление о составлении математической модели реальной ситуации. Уметь решать проблемные задачи и ситуации | Построение алгоритма действия, решение упражнений | §7, № 7.28(а,г), 7.31. |
|
|
| 21 | Степень
с отрицательным целым показателем | Комбинированный
|
Степень с натуральным показателем, степень с отрицательным показателем, умножение, деление и возведение в степень степени числа | Выполнение более сложных преобразований выражений, содержащих степень с отрицательным показателем. Умение доказывать тождества; | Иметь представление о степени с натуральным показателем, о степени с отрицательным показателем, умножении, делении и возведении в степень степени числа | Составление опорного конспекта, решение задач | §8, №8.13(а,б), 8.15, 8.17(б,г). |
|
|
| 22 | Степень
с отрицательным целым показателем | Проблемное изложение | Выполнение более сложных преобразований выражений, содержащих степень с отрицательным показателем. Умение доказывать тождества | Уметь: – упрощать выражения, используя определение степени с отрицательным показателем и свойства степени; – составлять текст научного стиля | Фронтальный опрос; решение развивающих задач
| §8, №8.19(а), 8.22, 8.24(б). |
|
|
| 23 | Степень
с отрицательным целым показателем | Контроль, обобщение и коррекция знаний |
| Умение самостоятельно выбрать рациональный способ преобразования рациональных выражений, доказывать тождества, решать рациональные уравнения способом освобождения от знаменателей, составляя математическую модель реальной ситуации | Уметь: – демонстрировать теоретические знания по теме «Алгебраические дроби»; – излагать информацию, интерпретируя факты, разъясняя значение и смысл теории | Индивидуальный опрос по теоретическому материалу | §8, Домашняя контрольная работа №18 (стр.51-53). |
|
|
| 24 | Контрольная работа №2 по теме «Алгебраические дроби» | Контроль, оценка
знаний |
|
| Уметь: – расширять и обобщать знания об упрощении выражений, сложении и вычитании, умножении и делении алгебраических дробей с разными знаменателями; – владеть навыками контроля и оценки своей деятельности | Индивидуальное решение контрольных
заданий |
|
|
|
| 25 | Анализ контрольной работы. Функция
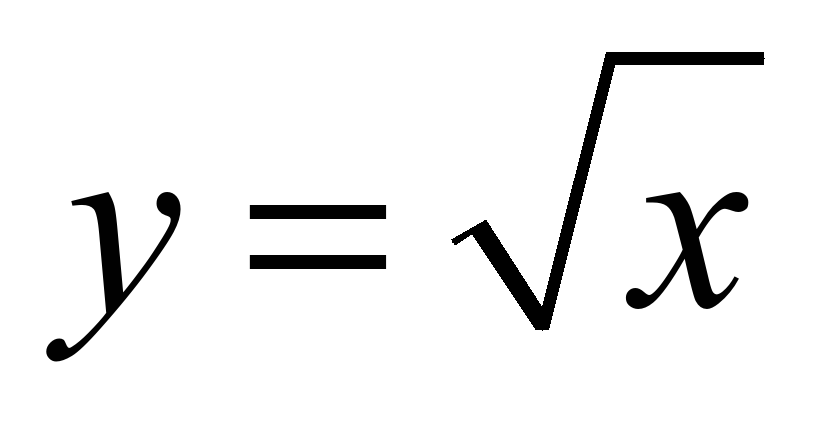 . Свойства . Свойства
квадратного корня Рациональные числа | Комбинированный | Множество рациональных чисел, знак принадлежности, знак включения, символы математического языка, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешанно периодическая дробь | Запись любого рационального числа в виде конечной десятичной дроби и наоборот; | Знать понятие
рациональные числа, бесконечная десятичная периодическая дробь. Уметь определять понятия, приводить доказательства | Индивидуальный опрос; выполнение упражнений
по образцу | §9, №9.16, 9.18, 9.22. |
|
|
| 26 | Понятие
квадратного корня из неотрицательного числа | Комбинированный | Квадратный корень, квадратный корень из неотрицательного числа, подкоренное выражение, извлечение квадратного корня, иррациональные числа, кубический корень | Квадратные уравнения, корнями которого являются иррациональные числа, простейшие иррациональные уравнения; | Знать действительные и иррациональные числа | Индивидуальный опрос; выполнение упражнений
по образцу | §10, №10.5, 10.17, 10.218. |
|
|
| 27 | Понятие
квадратного корня из неотрицательного числа | Комбинированный | Квадратный корень из неотрицательного числа, корень n-й степени из неотрицательного числа | Квадратные уравнения, корнями которого являются иррациональные числа, простейшие иррациональные уравнения; | Уметь: – извлекать квадратные корни из неотрицательного числа;
| Индивидуальный опрос; выполнение упражнений
по образцу | §10, №10.19, 10.28, 10.388 |
|
|
| 28 | Иррациональные числа | Комбинированный | Иррациональные числа, бесконечная десятичная непериодическая дробь, иррациональные выражения | Доказательство иррациональности числа; | Иметь представление о понятии «иррациональное число». Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах | Работа с конспектом, с книгой и наглядными пособиями по группам
| §11, №11.5, 11.8. |
|
|
| 29 | Множество действительных чисел | Проблемное изложение | Множество действительных чисел, сравнение действительных чисел, действия над действительными числами | Делимость целых чисел; деление
с остатком. Умение решать задачи с целочисленными неизвестными;
| Знать о делимости целых чисел; о делении с остатком. Уметь: – решать задачи
с целочисленными неизвестными; – объяснить изученные положения на самостоятельно подобранных конкретных примерах | Взаимопроверка в парах; тренировочные упражнения | §12, №12.16, 12.218. |
|
|
| 30 | Функция
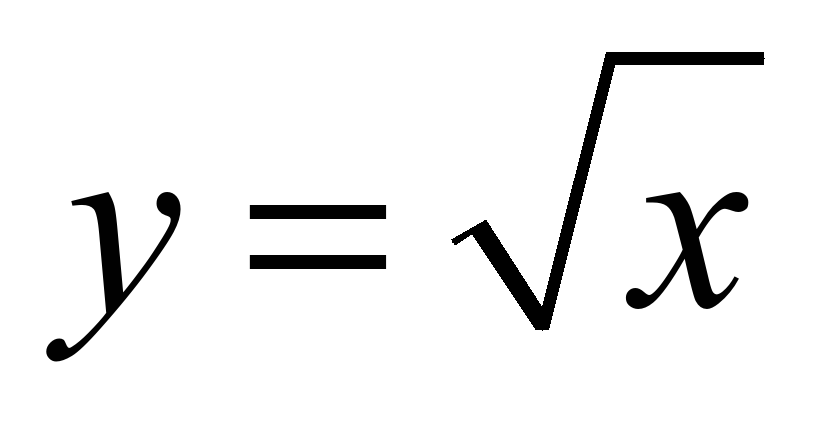 , ,
ее свойства
и график | Проблемное изложение
| Функция
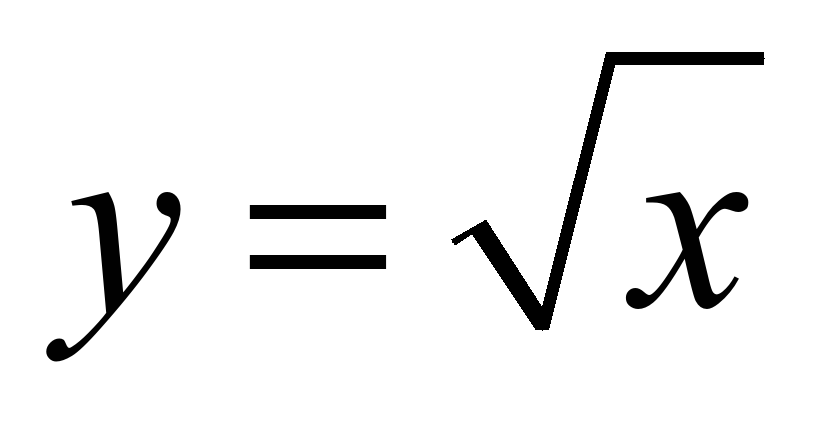 , график функции , график функции
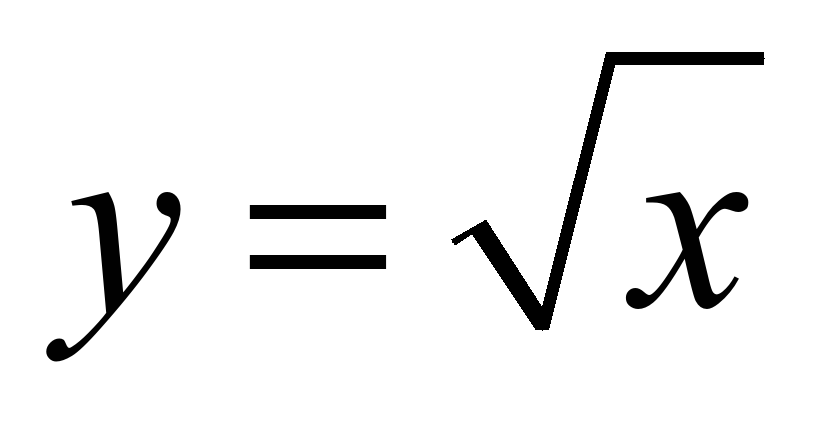 , свойства функции , свойства функции 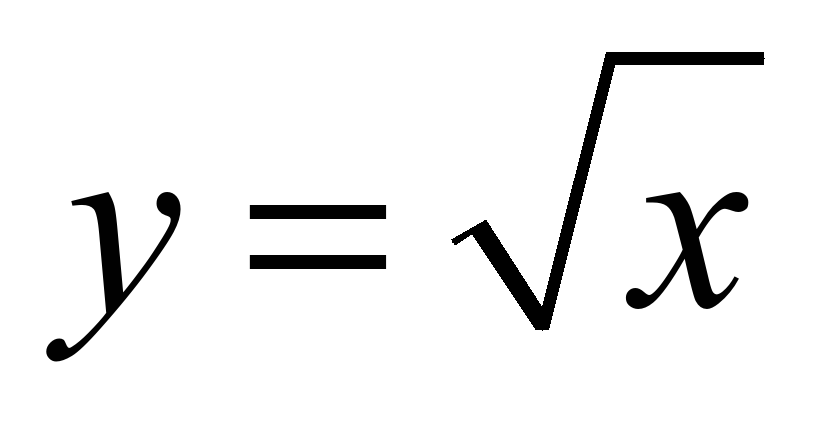 |
Умение читать графики функций, решать графически уравнения и системы уравнений; | Уметь: – строить график функции 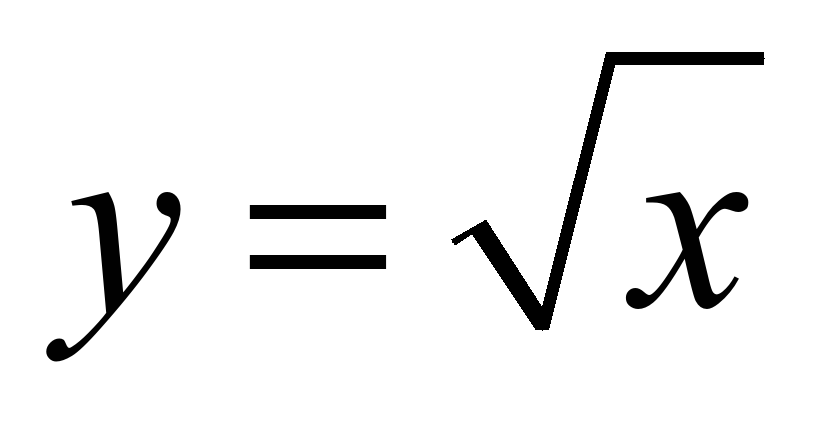 , ,
знать её свойства;
| Взаимопроверка в парах; тренировочные упражнения | §13, №13.6, 13.11(а,г), 13.24(б)8. |
|
|
| 31 | Функция
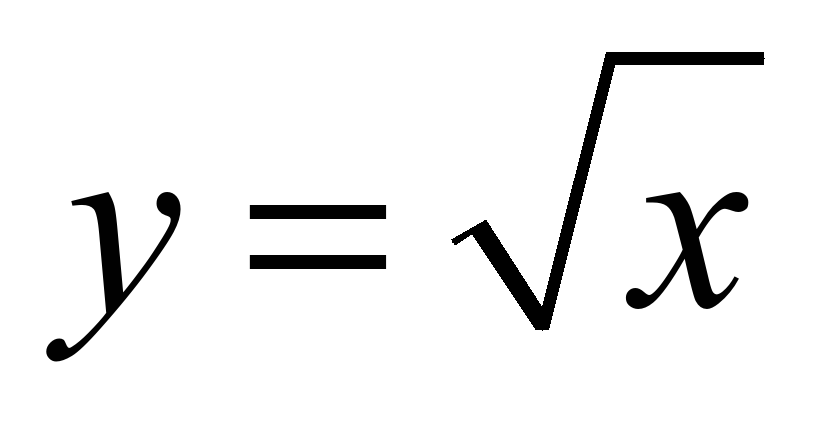 , ,
ее свойства
и график | Комбинированный | функция, выпуклая вверх, функция, выпуклая вниз | Индивидуальный опрос; выполнение упражнений
по образцу | §13, №13.17, 13.20, 13.29(г)8. |
|
|
| 32 | Свойства
квадратных корней | Комбинированный | Квадратный корень из произведения, квадратный корень из дроби,
вычисление корней
| Выполнение более сложных упрощений выражений наиболее рациональным способом. | Знать свойства квадратных корней. Уметь: – применять данные свойства корней при нахождении значения выражений; – добывать информацию по заданной теме в источниках различного типа | Работа с конспектом, с книгой и наглядными пособиями по группам
| §14, №14.4, 14.8, 14.11(а,б). |
|
|
| 33 | Свойства
квадратных корней | Поисковый
| Умение вычислять значения квадратных корней, не используя таблицу квадратов чисел; решать функциональные уравнения; | Уметь: – применять свойства квадратных корней для упрощения выражений и вычисления корней; – формировать
вопросы, задачи,
создавать проблемную ситуацию | Проблемные задания, фронтальный опрос, решение упражнения | §14, №14.18, 14.22, 14.298. |
|
|
| 34 | Преобразование выражений, содержащих операцию извлечения квадратного корня | Комбинированный
| Преобразование выражений, содержащих операцию извлечения квадратного корня, освобождение от иррациональности в знаменателе | Умение оценивать неизвлекающиеся корни, находить их приближённые значения; самостоятельно искать и отбирать необходимую для решения учебных задач информацию; | Иметь представление о преобразовании выражений, об операциях извлечения квадратного корня и освобождении от иррациональности в знаменателе | Проблемные задачи, фронтальный опрос, упражнения | §15, №15.2, 15.7, 15.10. |
|
|
| 35 | Преобразование выражений, содержащих операцию извлечения квадратного корня | Поисковый
| Умение раскладывать выражения на множители способом группировки, используя определение и свойства квадратного корня; | Знать о преобразовании выражений, об операциях извлечения квадратного корня и освобождение от иррациональности в знаменателе. Уметь развернуто обосновывать суждения | Проблемные задания, работа с раздаточным материалом
| §15, №15.22, 15.24, 15.25(г). |
|
|
| 36 | Преобразование выражений, содержащих операцию извлечения квадратного корня | Проблемный
| Умение раскладывать выражения на множители, используя формулу квадрата суммы и разности; | Уметь выполнять преобразования, содержащие операцию извлечения корня, освобождаться от иррациональности в знаменателе | Практикум,
индивидуальный опрос | §15, №15.26(б), 5.30(а, б), 15.368. |
|
|
| 37 | Преобразование выражений, содержащих операцию извлечения квадратного корня | Исследовательский
| Умение сокращать дроби, раскладывая выражения на множители, освобождаться от иррациональности в знаменателе;
| Уметь: – выполнять преобразования, содержащие операцию извлечения корня, освобождаться от иррациональности в знаменателе; – находить и использовать информацию | Проблемные задания, ответы на вопросы
| §15, №15.41, 15.49(б,г), 15.69(г)8 |
|
|
| 38 | Контрольная работа №3 по теме «Функция 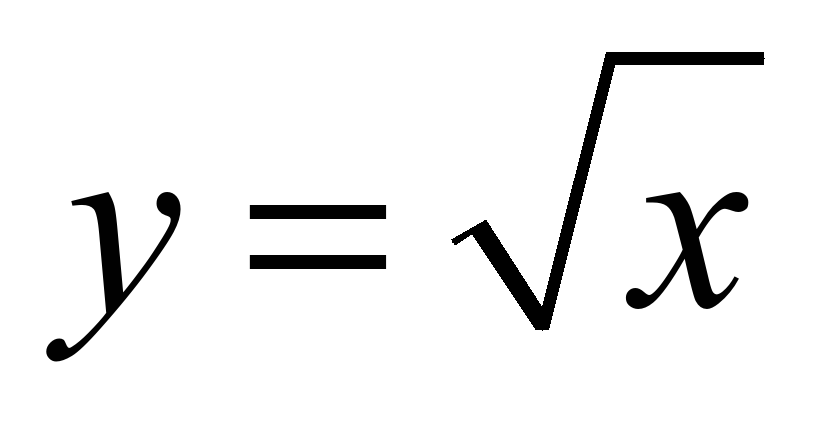 . Квадратные корни» . Квадратные корни» | Контроль, оценка
знаний |
|
| Уметь: – расширять и обобщать знания о преобразовании выражений, содержащих операцию извлечения квадратного корня, применяя свойства квадратных корней | Индивидуальное решение контрольных
заданий |
|
|
|
| 39 | Анализ контрольной работы. Модуль действительного числа | Комбинированный | Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного числа, совокупность уравнений, тождество 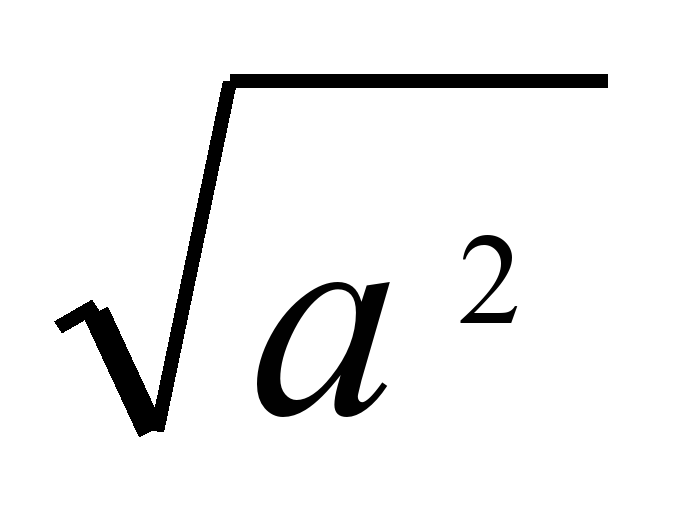 = а = а | Умение доказывать свойства модуля и решать модульные неравенства; ТС - составить набор карточек с заданиями. | Иметь представление об определении модуля действительного числа. Уметь: – применять свойства модуля; – составлять текст научного стиля; – находить и использовать информацию | Работа с опорными конспектами, раздаточным материалом | §16, №16.6, 16.9, 16.15. |
|
|
| 40 | Модуль действительного числа | Комбинированный |
|
| Работа с опорными конспектами, раздаточным материалом | §16, №16.18, 16.21(а,в), 16.258. |
|
|
| 41 | Модуль действительного числа
| Учебный практикум
| Умение доказывать свойства модуля и решать модульные неравенства; | Знать определение модуля действительного числа. Уметь: – применять свойства модуля; – развернуто обосновывать суждения; – проводить самооценку собственных действий
| Практикум, индивидуальный опрос, работа с наглядными пособиями | §16, №16.29(а), 16.31(в), 16.32(а,г). |
|
|
| 42 | Функция y = kx2, ее свойства и график | Комбинированный
| Кусочно-заданные функции, контрольные точки графика, парабола, вершина параболы, ось симметрии параболы, фокус параболы, функция y = kx2, график функции
y = kx2 | Графическое решение уравнения и системы уравнений, определение числа решений системы уравнений с помощью графического метода; | Иметь представления о функции вида y = kx2, о ее графике и свойствах. Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах | Практикум,
фронтальный опрос; математический диктант | §17, №17.4, 17.6, 17.10. |
|
|
| 43 | Функция y = kx2, ее свойства и график | Комбинированный
| Упрощение функциональных выражения, построение графиков кусочно- заданных функций; | Знать свойства функции и их описание по графику функции.
| Работа с опорными конспектами, раздаточным материалом | §17, №17.12, 17.19, 17.27*. |
|
|
| 44 | Функция y = kx2,
ее свойства и график | Поисковый
| Упрощение функциональных выражения, построение графиков кусочно- заданных функций | Уметь: – строить график функции y = kx2; – добывать информацию по заданной теме в источниках различного типа | Работа с опорными конспектами, раздаточным материалом | §17, №17.23, 17.29(а,в), 17.35*. |
|
|
| 45 | Функция
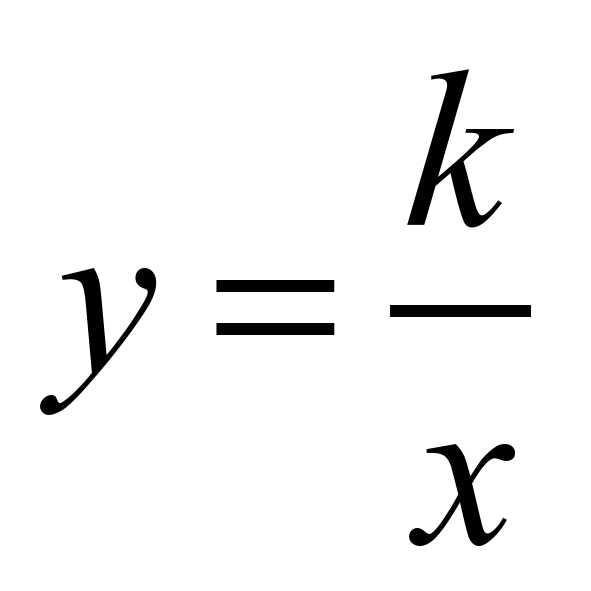 , ,
ее свойства
и график | Комбинированный
| Функция
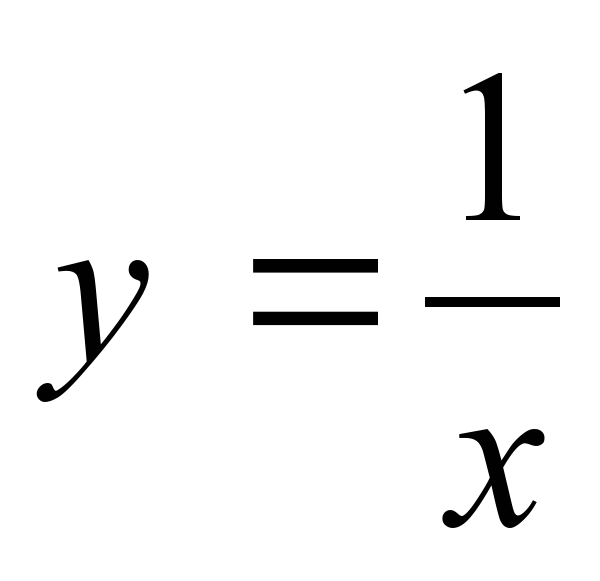 , гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы, функция , гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы, функция 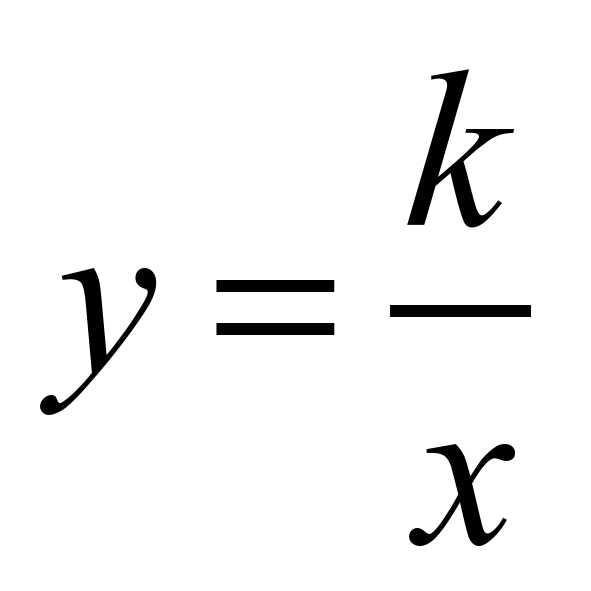 | Упрощение функциональных выражения, построение графиков кусочно- заданных функций | Иметь представления о функции вида 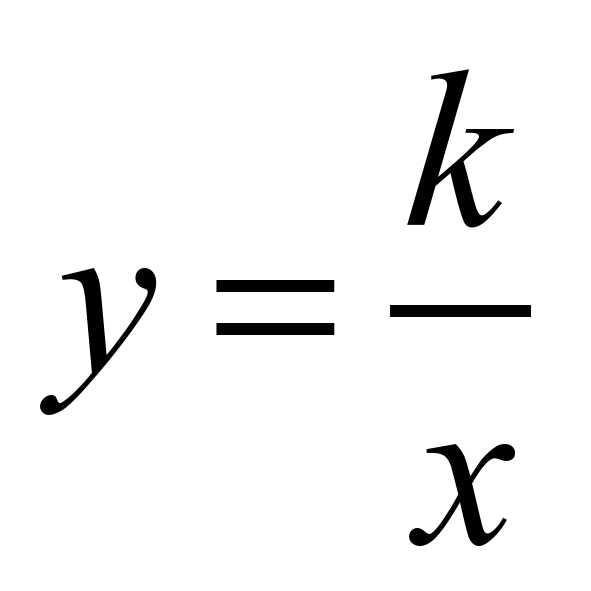 , о ее графике и свойствах. , о ее графике и свойствах. Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах | Фронтальный опрос; решение качественных задач | §18, №18.5, 18.11, 18.14. |
|
|
| 46 | Функция
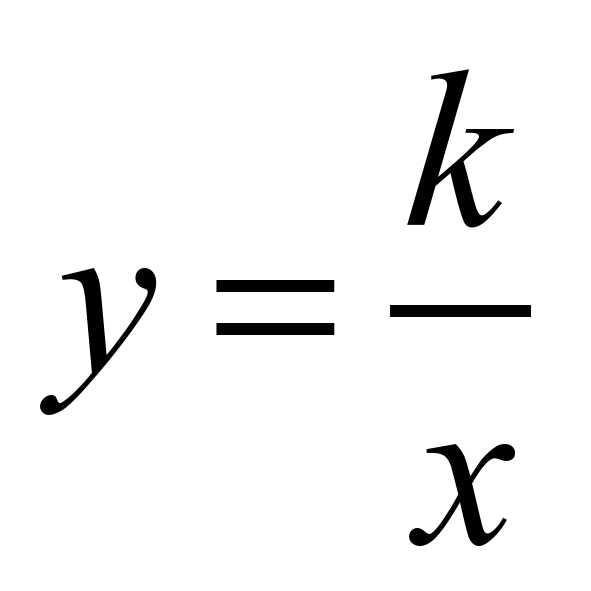 , ,
ее свойства
и график | Учебный практикум
| обратная пропорциональность, коэффициент обратной пропорциональности, свойства функции 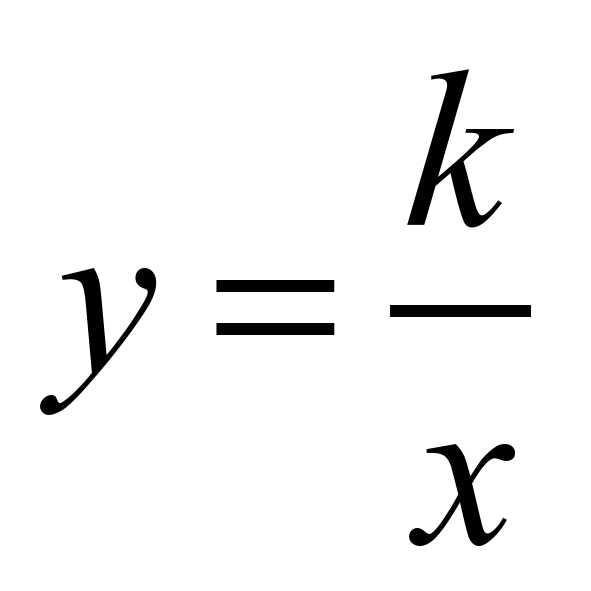 область значений функции, окрестность точки, точка максимума, точка минимума область значений функции, окрестность точки, точка максимума, точка минимума | Упрощение функциональных выражения, построение графиков кусочно- заданных функций | Знать свойства функции и их описание по графику функции. Уметь: – строить график функции 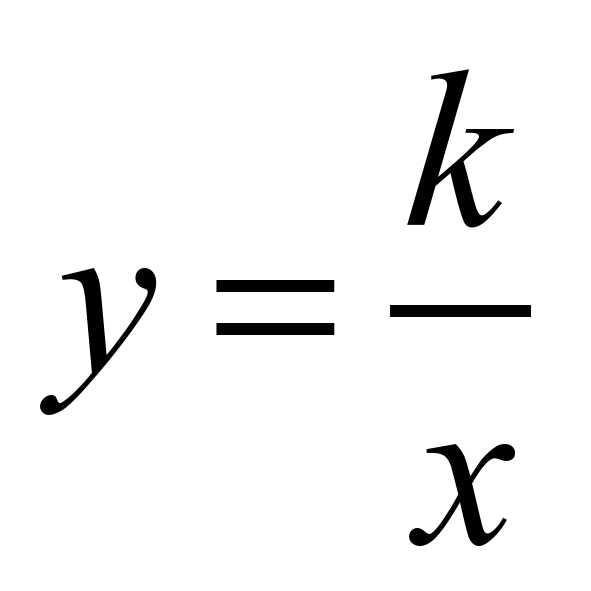 ; ;
| Построение алгоритма действия, решение упражнений | §18, №18.22 Домашняя контрольная работа №2* (стр.94-96). |
|
|
| 47 | Контрольная работа №4 по теме «Функция y = kx2, 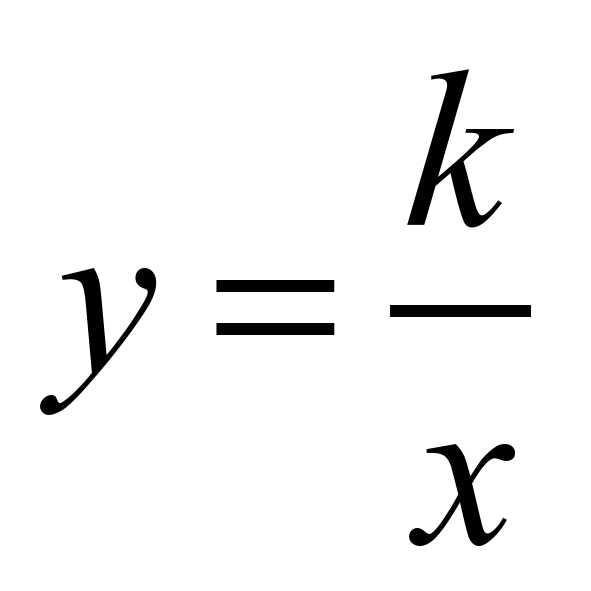 » »
| Контроль, оценка
знаний |
| Графическое решение уравнения и системы уравнений, определение числа решений системы уравнений с помощью графического метода; упрощение функциональных выражения, построение графиков кусочно- заданных функций | Знать свойства функции и их описание по графику построенной функции. Уметь: – строить графики функции
| Индивидуальное решение контрольных
заданий |
|
|
|
| 48 | Анализ контрольной работы. Как построить график функции
y = f(x + l),
если известен график
функции
y = f(x) | Комбинированный | Параллельный перенос, параллельный перенос вправо (влево), | Умение по алгоритму построить график функции
y = f(x + l), прочитать его и описать свойства; | Иметь представление, как с помощью параллельного переноса вправо или влево построить график функции y = f(x + l). | Взаимопроверка в парах; работа с текстом
| §19, №19.5, 19.11(б,г), 19.15. |
|
|
| 49 | Как построить график функции
y = f(x + l),
если известен график
функции
y = f(x) | Комбинированный | вспомогательная система координат, алгоритм построения графика функции
y = f(x + l) | Умение по алгоритму построить график функции
y = f(x + l), прочитать его и описать свойства; | Уметь строить графики с помощью параллельного переноса вправо (влево) | Взаимопроверка в парах; работа с текстом
| §19, №19.19, 19.22, 19.33*. |
|
|
| 50 | Как построить график функции
y = f(x) + m, если известен график функции
y = f(x) | Комбинированный | Параллельный перенос, параллельный
перенос верх (вниз), вспомогательная система координат, | Умение по алгоритму построить график функции
y = f(x) + m, прочитать его
и описать свойства; самостоятельно искать и выбирать необходимую для решения учебных задач информацию; | Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции y = f(x) + m.
| Взаимопроверка в парах; составление
опорного
конспекта | §20, №20.2, 20.7(б,г), 20.11. |
|
|
| 51 | Как построить график функции
y = f(x) + m, если известен график функции
y = f(x) | Комбинированный | алгоритм построения графика функции
y = f(x) + m | Излагать информацию, обосновывая свой собственный подход | Уметь строить графики с помощью параллельного переноса вверх (вниз) | Взаимопроверка в парах; составление
опорного
конспекта | §20, №20.15, 20.23, 20.33*. |
|
|
| 52 | Как построить график функции y = = f(x + l) + m, если известен график функции
y = f(x) | Комбинированный | Параллельный перенос, параллельный перенос вправо (влево), параллельный перенос вверх (вниз), | -Умение по алгоритму построить график функции y = f(x + l) + m, прочитать его и описать свойства; строить кусочно-заданные функции; ПиИД -объяснить изученные положения на самостоятельно подобранных конкретных примерах | Иметь представление, как с помощью параллельного переноса построить график функции
y = f(x + l) + m.
| Практикум, фронтальный опрос, работа с раздаточным матери-
алом | §21, №21.2(б,в), 21.5, 21.12. |
|
|
| 53 | Как построить график функции y = = f(x + l) + m, если известен график функции
y = f(x) | Комбинированный
| вспомогательная система координат, алгоритм постро-ения графика функции
y = f(x + l) + m | Умение решать графически систему уравнений, строить график функции вида y = a(x + l)2 + m; | Уметь: – строить график функции вида
y = f(x + l) + m,
описывать свойства функции по ее графику;
| Работа с опорными конспектами, раздаточным материалом
| §21, №21.15, 21.20, 21.26(б)*. |
|
|
| 54 | Функция y = ax2 + bx + c,
ее свойства и график | Поисковый
| Функция y =
= ax2 + bx + c, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы y = ax2 + bx+ +c | Умение переходить с языка формул на язык графиков и наоборот; определять число корней уравнения и системы уравнений; | Иметь представление о функции
y = ax2 + bx + c,
о ее графике и свойствах.
| Фронтальный опрос; решение качественных задач | §22, №22.7, 22.13, 22.16. |
|
|
| 55 | Функция y = ax2 + bx + c,
ее свойства и график | Комбинированный | Умение переходить с языка формул на язык графиков и наоборот; определять число корней уравнения и системы | Уметь: – строить графики, заданные таблично и формулой;
| Взаимопроверка в парах; составление
опорного
конспекта | §22, №22.18, 22.24, 22.28. |
|
|
| 56 | Функция y = ax2 + bx + c,
ее свойства и график | Комбинированный | -Умение упрощать функциональные выражения, находить значения коэффициентов в формуле функции
y = ax2 + bx + c, без построения графика функции | Уметь: – строить график функции
y = ax2 + bx + c,
описывать свойства по графику; | Построение алгоритма действия, решение упражнений | §22, №22.30, 22.41, 22.45*. |
|
|
| 57 | Графическое решение квадратных уравнений | Учебный практикум
| Квадратное уравнение, несколько способов графического решения уравнения | Умение свободно применять несколько способов графического решения уравнений; собрать материал для сообщения по заданной теме; составить набор карточек с заданиями | Знать графические способы решения квадратных уравнений, применять на практике.
| Взаимопроверка в парах; работа с текстом | §23, №23.4, 23.9, 23.20. |
|
|
| 58 | Квадратичная функция. Функция 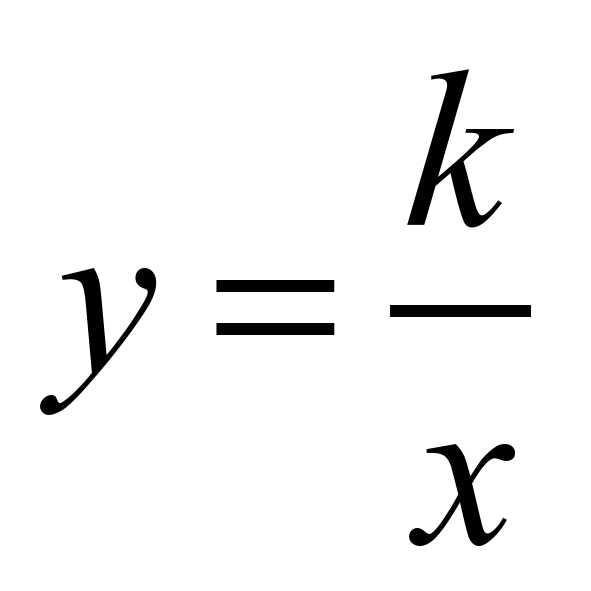 » » | Комбинированный
|
| Умение свободно излагать теоретический материал по теме «Квадратичная функция и функция обратной пропорциональности»; | Уметь: применять теоретические знания по теме «Квадратичная функция и функция обратной пропорциональности» для решения практических задач
| Индивидуальный опрос по теоретическому материалу | Домашняя контрольная работа №3* (стр.147-148). |
|
|
| 59 | Контрольная работа №5 по теме «Квадратичная функция. Функция 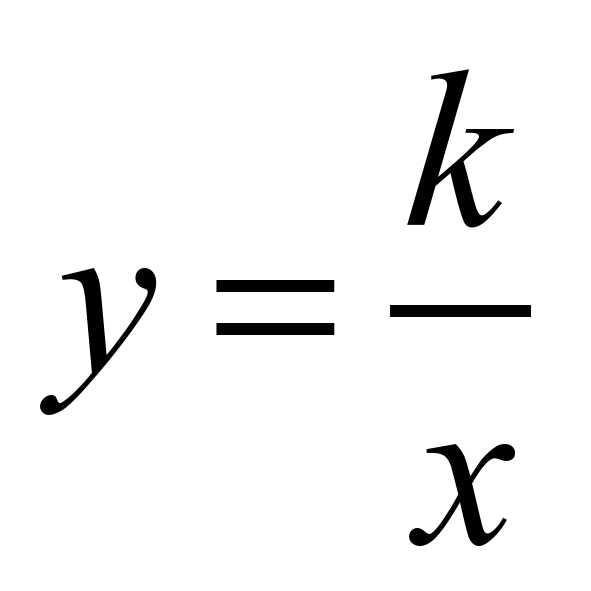 » » | Контроль, оценка
знаний |
|
| Уметь: – расширять и обобщать знания об использовании алгоритма построения графика функции
| Индивидуальное решение контрольных заданий |
|
|
|
| 60 | Анализ контрольной работы. Квадратные уравнения. Основные
понятия | Поисковый | Квадратное уравнение, старший коэффициент, второй коэффициент, свободный член, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения | Квадратные уравнения: приведенные полные, не приведенные полные, неполные; | Иметь представление о полном и неполном квадратном уравнении, о решении неполного квадратного уравнения. Уметь найти и устранить причины возникших трудностей | Проблемные задания, фронтальный опрос, упражнения | §24, №24.2, 24.5, 24.8. |
|
|
| 61 | Квадратные уравнения. Основные
понятия | Комбинированный
| Рациональные уравнения и задачи на составление рациональных уравнений; | Уметь решать
неполные квадратные уравнения и полные квадратные уравнения, разложив его левую часть на множители | Практикум,
индивидуальный опрос
| §24, №24.16, 24.25, 24.34*. |
|
|
| 62 | Формулы
корней квадратного уравнения | Комбинированный
| Формулы корней квадратного уравнения, если второй коэффициент четный; | Иметь представление о дискриминанте квадратного уравнения, формулах корней квадратного уравнения, об алгоритме решения квадратного уравнения | Работа с конспектом, книгой и наглядными пособиями по группам | §25, №25.5(а,б), 25.9(в), 25.22*. |
|
|
| 63 | Формулы
корней квадратного уравнения | Поисковый
| Простейшие квадратные уравнения с параметрами; исследование всех корней квадратного уравнения с параметром; | Знать алгоритм вычисления корней квадратного уравнения, используя дискриминант. Уметь решать квадратные уравнения по алгоритму, привести примеры, подобрать аргументы, сформулировать выводы | Проблемные задания, фронтальный опрос, решение упражнений | §25, №25.18(а), 25.23, 25.37(в)*. |
|
|
| 64 | Формулы
корней квадратного уравнения | Учебный практикум
| Задачи
на составление квадратных уравнений; оценка информации, фактов, процессов, определение их актуальности; | Уметь: решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант;
| Работа с конспектом, с книгой и наглядными пособиями по группам | §25, №25.20(г), 25.32, 25.46(б)*. |
|
|
| 65 | Рациональные уравнения | Комбинированный
| Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней уравнения, посторонние корни | Решение рациональных уравнений, используя метод введения новой переменной.
| Иметь представление о рациональных уравнениях и об их решении.
| Взаимопроверка в парах; тренировочные упражнения | §26, №26.3, 26.6(б,в), 26.8(г). |
|
|
| 66 | Рациональные уравнения | Проблемное изложение | Решение рациональных уравнений, используя метод введения новой переменной.
| Знать алгоритм решения рациональных уравнений. Уметь отделить основную информацию от второстепенной | Проблемные задания, фронтальный опрос, упражнения | §26, №26.10(в), 26.12(б), 26.14(в,г). |
|
|
| 67 | Рациональные уравнения | Комбинированный
| Решение биквадратных уравнений, уравнений
с применением нескольких способов упрощения выражений, входящих
в уравнение. | Уметь: решать рациональные уравнения по заданному алгоритму и методом введения новой переменной; формировать вопросы, задачи, создавать проблемную ситуацию | Взаимопроверка в парах; тренировочные упражнения | §26, №26.17(а), 26.19(в), 26.25(г). |
|
|
| 68 | Контрольная работа №6 по теме «Квадратные уравнения» | Контроль, оценка
знаний |
|
| Уметь: решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант; решать рациональные уравнения по заданному алгоритму и методом введения новой переменной | Индивидуальное решение контрольных заданий |
|
|
|
| 69 | Анализ контрольной работы. Рациональные уравнения как математические модели реальных ситуаций | Комбинированный
| Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений | Решение задач на числа с выделением основных этапов математического моделирования. Использование для решения познавательных задач справочной литературы | Уметь: решать задачи
на числа, выделяя
основные этапы математического моделирования; привести примеры, подобрать аргументы, сформулировать выводы | Работа с конспектом, с книгой и наглядными пособиями по группам | §27, №27.2, 27.6, 27.10. |
|
|
| 70 | Рациональные уравнения как математические модели реальных ситуаций | Поисковый
| Решение задач на движение по дороге, выделение основных этапов математического моделирования.
| Уметь: решать задачи
на движение по дороге, выделяя основные этапы математического моделирования; участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение | Проблемные задания; взаимопроверка в парах; решение упражнения | §27, №27.13, 27.15, 27.18. |
|
|
| 71 | Рациональные уравнения как математические модели реальных ситуаций | Учебный практикум |
Решение задач на движение по воде с выделением основных этапов математического моделирования. |
Уметь: решать задачи
на движение по воде, выделяя основные этапы математического моделирования; | Фронтальный опрос; выборочный диктант; | §27, №27.20, 27.23, 27.27*. |
|
|
| 72 | Рациональные уравнения как математические модели реальных ситуаций | Учебный практикум | Решение качественных задач | §27, №27.33, 27.38, 27.41*. |
|
|
| 73 | Еще одна формула корней квадратного уравнения
| Поисковый
|
Квадратное уравнение
с четным вторым коэффициентом, формулы корней квадратного уравнения с четным вторым коэффициентом | Простейшие квадратные уравнения с четным вторым коэффициентом с параметрами; исследование всех корней квадратного уравнения с четным вторым коэффициентом с параметром; | Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант. Уметь: решать квадратные уравнения с четным вторым коэффициентом по алгоритму;
привести примеры, подобрать аргументы, сформулировать выводы | Проблемные задания, фронтальный опрос, упражнения | §28, №28.2(в), 28.6(а,г), 28.8. |
|
|
| 74 | Еще одна формула корней квадратного уравнения | Комбинированный
| Задачи на составление квадратных уравнений с четным вторым коэффициентом; | Уметь: решать квадратные уравнения с четным вторым коэффициентом по формулам корней квадратного уравнения с четным вторым коэффициентом через дискриминант; | Практикум, индивидуальный опрос | §28, №28.15, 28.19(в,г), 28.21(б). |
|
|
| 75 | Теорема Виета | Комбинированный | Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными
| Умение составлять квадратные уравнения по его корням, раскладывать на множители квадратный трехчлен; | Иметь представление о теореме Виета и об обратной теореме Виета, о симметрических выражениях с двумя переменными.
| Фронтальный опрос; решение качественных задач | §29, №29.6, 29.9(в,г), 29.13. |
|
|
| 76 | Теорема Виета | Учебный практикум
| Обратная теорема Виета | Уметь: применять теорему Виета и обратную теорему Виета, решая квадратные уравнения; | Построение алгоритма действия, решение упражнений
| §29, №29.15(в), 29.21(а,в), 29.22(а). |
|
|
| 77 | Контрольная работа №7 по теме «Квадратные и рациональные уравнения» | Контроль, оценка
знаний |
|
| Уметь: решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант, теорему Виета; решать рациональные уравнения по заданному алгоритму и методом введения новой переменной | Индивидуальное решение контрольных заданий | §30, №30.1, 30.6(в,г), 30.10(в). |
|
|
| 78 | Анализ контрольной работы. Иррациональные уравнения | Проблемный | Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнения, | Умение решать иррациональные уравнения, совершая равносильные переходы в преобразованиях; | Иметь представление об иррациональных уравнениях, о равносильных уравнениях, о равносильных преобразованиях уравнений, о неравносильных преобразованиях уравнения | Проблемные задачи, индивидуальный опрос | §30, №30.12(б), 30.14(б,г), 30.16(а,б). |
|
|
| 79 | Иррациональные уравнения | Комбинированный | неравносильные преобразования уравнения | Иррациональные уравнения, равносильные переходы в преобразованиях; проверка корней, получившихся при неравносильных преобразованиях; | Уметь: решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований;
| Практикум, фронтальный опрос, работа с раздаточным материалом | §30, №30.19(в), 30.8(б,г), 30.18(в). |
|
|
| 80 | Иррациональные уравнения | Контроль, обобщение | Иррациональные уравнения, равносильные переходы в преобразованиях; проверка корней, получившихся при неравносильных преобразованиях; | Уметь: демонстрировать теоретические знания по теме «Квадратные уравнения»; излагать информацию, интерпретируя факты, разъясняя значение и смысл теории | Индивидуальный опрос по теоретическому материалу | §30, №30.20(г), 30.22(в), 30.23(а). |
|
|
| 81 | Свойства числовых
неравенств | Комбинированный
| Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши | Умение выполнять действия с числовыми неравенствами; доказывать справедливость числовых неравенств при любых значениях переменных; Умение доказать справедливость числового неравенства методом выделения квадрата двучлена и используя неравенство Коши; собрать материал для сообщения по заданной теме | Знать свойства числовых неравенств.
| Работа с конспектом, с книгой и наглядными пособиями
по группам | §31.№ 31.7 – 31.9(в,г); 31.12 ; 31.24* |
|
|
| 82 | Свойства числовых
неравенств | Поисковый
| Иметь представление о неравенстве одинакового смысла, противоположного смысла, о среднем арифметическом и геометрическом, о неравенстве Коши | Проблемные задания, фронтальный опрос, решение упражнения | §31.№ 31.39 – 31.45(в,г); 31.36* |
|
|
| 83 | Свойства числовых
неравенств | Комбинированный
| Уметь: применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств; формировать вопросы, задачи, создавать проблемную ситуацию | Работа с конспектом, с книгой и наглядными пособиями
по группам |
§31.№ 31.49; 31.52 – 31.56 (в,г); 31.57 – 31.65* |
|
|
| 84 | Исследование функции на монотонность | Комбинированный | Монотонная, возрастающая и убывающая на промежутке функции. Построение кусочных функций и чтение их графиков. | Умение исследовать различные функции на монотонность; решать уравнения, используя свойство монотонности; | Иметь представление о возрастающей, убывающей, монотонной функции на промежутке.
| Составление опорного конспекта, решение задач | §31, №31.26, 31.29, 31.40*. |
|
|
| 85 | Исследование функции на монотонность | Проблемное изложение | Умение исследовать кусочно-заданные функции на монотонность; решать уравнения и неравенства, | Уметь построить график
и исследовать на монотонность функции: линейную, квадратичную, обратную пропорциональность, функцию корень квадратный из х | Фронтальный опрос; решение развивающих задач | §32, .№ 32.12; 32.14 |
|
|
| 86 | Исследование функции на монотонность | Проблемное изложение | Фронтальный опрос; решение развивающих задач | §32, №32.6, 32.11. |
|
|
| 87 | Решение линейных
неравенств | Комбинированный
| Неравенство
с переменной, решение неравенства с переменной, множество решений, система линейных неравенств, пересечение решений неравенств системы |
Геометрический смысл линейного неравенства с двумя переменными. | Иметь представление о неравенстве с переменной, о системе линейных неравенств, пересечении решений неравенств системы.
| Работа с опорными конспектами, раздаточным материалом |
§33.№ 33.4 – 33.9 (в,г); 33.14 – 33.15 (в,г); |
|
|
| 88 | Решение линейных
неравенств | Учебный практикум
| Уметь: решать неравенства с переменной и системы неравенств с переменной;
| Практикум, индивидуальный опрос, работа с наглядными пособиями |
§33.№ 33.27 –33.30 (в,г); 33.36* |
|
|
| 89 | Решение квадратных
неравенств | Комбинированный
| Квадратное неравенство, знак объединения множеств, алгоритм решения квадратного неравенства, метод интервалов | Метод интервалов. Равносильность неравенств. Неравенства с параметрами | Иметь представление о квадратном неравенстве, о знаке объединения множеств, об алгоритме решения квадратного неравенства, о методе интервалов.
| Работа с конспектом, книгой и наглядными пособиями по группам | §34.№ 34.2 – 34.10 (в,г); |
|
|
| 90 | Решение квадратных
неравенств | Поисковый
|
Умение решать
квадратные неравенства методом интервалов. Представление о решении квадратичных неравенств с параметром.
| Знать, как решать квадратное неравенство по алгоритму и методом интервалов. Уметь самостоятельно искать и отбирать необходимую для решения учебных задач информацию | Проблемные задания; взаимопроверка в парах; решение упражнения
| §.34№ 34.11 – 34.18 (в,г); |
|
|
| 91 | Решение квадратных
неравенств | Учебный практикум
| Уметь: решать квадратные неравенства
по алгоритму и методом интервалов; дать оценку информации, фактам, процессам, определять их актуальность | Фронтальный опрос; выборочный диктант; решение качественных задач
| §34, №34.29, 34.34, 34.41(а,в)*. |
|
|
| 92 | Контрольная работа №8 по теме «Неравенства» | Контроль, оценка
знаний
|
|
| Уметь расширять
и обобщать знания
о числовых неравенствах, о неравенстве с одной переменной, о модуле действительного числа | Индивидуальное решение контрольных
заданий
|
|
|
|
| 93 | Анализ контрольной работы. Приближенное значение действительных чисел | Частично-поисковый
| Приближенное значение по недостатку, приближенное значение по избытку, | Приближенное значение по недостатку, по избытку, | Знать о приближенном значении по недостатку, по избытку, об округлении чисел, о погрешности приближения, абсолютной и относительной погрешностях. | Взаимопроверка в парах;
| §35, №35.1, 35.4, 35.6. |
|
|
| 94 | Приближенное значение действительных чисел | Частично-поисковый
| округление чисел, погрешность приближения, абсолютная погрешность, правило округления, относительная погрешность | Округление чисел,
погрешности приближения, абсолютная и относительная погрешности | работа с опорным материалом | §35, №35.8, 35.10(а,б). |
|
|
| 95 | Стандартный вид числа
| Комбинированный
| Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме
| Умение использовать знания о стандартном виде положительного числа, о порядке числа, о записи числа в стандартном виде | Знать формулу стандартного вида положительного числа, иметь представление о порядке числа, о записи числа в стандартном виде | Взаимопроверка в группе; практикум
| §36, №36.5, 36.9, 36.15(б). |
|
|
| 96 | Повторение. Алгебраические дроби
| Комбинированный
| Преобразование рациональных
выражений,
решение рациональных уравнений
| Умение доказывать тождества, решать рациональные уравнения, задачи, выделяя три этапа математического моделирования | Уметь: применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении; находить значение дроби при заданном значении переменной преобразовывать рациональные выражения, используя все действия с алгебраическими дробями;
| Взаимопроверка в группе; решение логических задач
| Гл.6. № 103-106 |
|
|
| 97 | Функции и их свойства. | Учебный практикум
| Функции и их графики | Исследование функции с помощью её графика, исследование на монотонность | Уметь выполнять построение графиков функций, проводить соответствующие исследования | Взаимопроверка в группе; практикум
| Гл.6,№ 32, 33, 45 |
|
|
| 98 | Преобразование рациональных выражений. | Комбинированный
| Преобразование рациональных выражений и выражений, содержащих операцию извлечения квадратного корня. | Освобождение от иррациональности в знаменателе | Уметь выполнять преобразование рациональных выражений и выражений, содержащих операцию извлечения квадратного корня. | Решение качественных задач; работа
с раздаточным материалом
|
|
|
|
| 99 | Решение уравнений. | Учебный практикум
| Формулы корней квадратного уравнения, теорема Виета, разложение квадратного трехчлена на множители
| Уравнения с параметрами | Уметь решать рациональные, иррациональные, квадратные уравнения с помощью алгоритмов и графическим методом. | работа
с раздаточным материалом
| Гл.6, №74, 78,81, 93. |
|
|
| 100 | Решение неравенств | Комбинированный
| Решение линейных и квадратных неравенств, исследование функции на монотонность
| Обобщённый метод интервалов | Иметь представление о решении линейных и квадратных неравенств с одной переменной. Знать, как проводить исследование функции на монотонность.
| Решение качественных задач; работа
с раздаточным материалом
| Гл.6, №141, 143, 147, 153 |
|
|
| 101 | Итоговая
контрольная работа
| Контроль, оценка
знаний
|
|
|
| Индивидуальное решение
контрольных
заданий
|
|
|
|
| 102 | Заключительный урок. Работа над ошибками. |
|
|
|
|
|
|
|
|




















