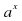Управление образования Администрации г. Усть-Илимска
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 9»
| Рассмотрена и одобрена на заседании предметной кафедры/МО «……» Руководитель ____________ФИО Протокол №… от…….2015 г. |
| «СОГЛАСОВАНО» Заместитель директорапо УВР МБОУ СОШ № 9 _________________ ФИО ________________2015 г. |
| «УТВЕРЖДАЮ» Директор МБОУ СОШ № 9 _____________ФИО __________________2015 г. |
Рабочая программа
по
алгебре и началам математического анализа
для 10 класса
(профильныйуровень)
Программа составлена на основе:
- Федерального компонента государственного стандарта общего образования (2004 г.);
- Авторской программы учебного предмета «Алгебра и начала анализа» С.М.Никольский («Программы общеобразовательных учреждений: Алгебра и начала математического анализа. 10-11 кл.»/ Сост. Т.А.Бурмистрова.- М. Просвещение. – 2010г.)
Разработчик программы:
учитель математики высшей квалификационной категории
Дрозд Л.В.
г.Усть-Илимск
2015/2016 уч. год
Пояснительная записка
Данная рабочая программа ориентирована на учащихся 10 классов и реализуется на основе следующих документов:
Федеральный компонент государственного образовательного стандарта, утвержденный Приказом Минобразования РФ № 1089 от 05.03.2004;
Программа для общеобразовательныхучрежедний:
Сборник “Программы общеобразовательных учреждений: Алгебра и начала математического анализа. 10-11 кл.”/ Сост. Т.А.Бурмистрова.- М. Просвещение. – 2010 г.
Учебник «Алгебра и начала математического анализа. 10 класс»: учеб.для общеобразовательных организаций: базовый и углубленный уровни/ [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. Просвещение, 2014 г.
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
При изучении курса математики на профильном уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
совершенствование проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решение широкого класса задач из различных разделов курса, развитие поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
планирование и осуществление алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использование самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнение расчетов практического характера;
построение и исследование математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
совершенствование самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
развитие представлений о вероятностно-статистических закономерностях в окружающем мире.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану на изучение предмета на профильном уровне отводится 4 часа в неделю, итого 136часов за учебный год, что соответствует учебному плану школы.В том числе контрольных работ - 10 часов. Используется учебник «Алгебра и начала математического анализа. 10 класс»: учеб.для общеобразовательных организаций: базовый и углубленный уровни/ [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. Просвещение, 2014 г.
Содержание:
Целые и действительные числа (12 часов).Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными. Понятие действительного числа. Свойства действительных чисел. Множества чисел и операции над множествами чисел. Доказательство неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач.
Рациональные уравнения и неравенства(18 часа, из них контрольные работы – 1 час). Рациональные выражения. Формула бинома Ньютона, свойства биноминальных коэффициентов, треугольник Паскаля, формулы разности и суммы степеней. Многочлены от одной переменной. Деление многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Решение целых алгебраических уравнений. Схема Горнера. Теорема Безу. Число корней многочлена.Рациональные уравнения и неравенства, системы рациональных неравенств.
Корень степени n(12 часов, из них контрольные работы – 1 час)Понятие функции, ее области определения и множества значений. Функция y = xn, где n N, ее свойства и график. Понятие корня степени n1 и его свойства, понятие арифметического корня.
N, ее свойства и график. Понятие корня степени n1 и его свойства, понятие арифметического корня.
Степень положительного числа (13 часов, из них контрольные работы – 1 час)Понятие степени с рациональным показателем, свойства степени с рациональным показателем. Понятие о пределе последовательности. Теоремы о пределах последовательностей. Существование предела монотонной и ограниченной. Ряды, бесконечная геометрическая прогрессия и ее сумма. Число e. Понятие степени с иррациональным показателем. Преобразование выражений, содержащих возведение в степень. Показательная функция, ее свойства и график.
Логарифмы (6 часов).Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени, переход к новому основанию. Десятичный и натуральный логарифмы. Преобразование выражений, содержащих логарифмы. Логарифмическая функция, ее свойства и график.
Простейшие показательные и логарифмические уравнения и неравенства методы их решения (11 часов, из них контрольные работы – 1 час). Показательные и логарифмические уравнения и неравенства и методы их решения.
Синус и косинус угла и числа (7часов).Радианная мера угла. Синус, косинус, тангенс и котангенс произвольного угла и действительного числа. Основное тригонометрическое тождество для синуса и косинуса. Понятия арксинуса, арккосинуса.
Тангенс и котангенс угла и числа (6 часов, из них контрольные работы – 1 час).Тангенс и котангенс угла и числа. Основные тригонометрические тождества для тангенса и котангенса. Понятие арктангенса и арккотангенса.
Формулы сложения(11 часов).Синус, косинус и тангенс суммы и разности двух аргументов. Формулы приведения. Синус и косинус двойного аргумента. Формулы половинного аргумента. Преобразование суммы тригонометрических функций в произведения и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование тригонометрических выражений.
Тригонометрические функции числового аргумента (9часов, из них контрольные работы – 1 час).Тригонометрические функции, их свойства и графики, периодичность, основной период.
Тригонометрические уравнения и неравенства (12 часов, из них контрольные работы – 1 час). Решение простейших тригонометрических уравнений и неравенств. Основные способы решения уравнений. Решение тригонометрических неравенств.
Элементы теории вероятностей (8 часов, из них практические работы – 1 час). Табличное и графическое представление данных. Числовые характеристики рядов данных. Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
Повторение курса алгебры и математического анализа за 10 класс (11 часов, из них контрольная работа– 1 часа).
Примерное поурочное планирование
| № пункта | Содержание учебного материала | Кол-во часов |
|
1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10
2.1 2.2 2.6 2.7 2.8 2.9 2.10 2.11
3.1 3.2 3.3 3.4 3.5 3.6 3.7
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
5.1 5.2 5.3
6.1 6.2 6.3 6.4 6.5 6.6
7.1, 7.2 7.3 7.4 7.5 7.6
8.1 8.2 8.3 8.4
9.1 9.2 9.3 9.4 9.5 9.6 9.7
10.1 10.2 10.3 10.4
11.1 11.2 11.3
11.4 11.5 11.6 11.7 11.8
12.1 12.2 12.3 12.4 | Действительные числа.12ч. Понятие действительного числа Множества чисел. Свойства действительных чисел. Метод математической индукции Перестановки Размещения Сочетания Доказательство числовых неравенств Делимость целых чисел Сравнения по модулю m Задачи с целочисленными неизвестными Рациональные уравнения и неравенства.18ч. Рациональные выражения Формула бинома Ньютона, суммы и разности степеней. Рациональные уравнения Системы рациональных уравнений Метод интервалов решения неравенств Рациональные неравенства Нестрогие неравенства Системы рациональных неравенств. Контрольная работа № 1 Корень степени n.12ч. Понятие функции и её графика Функция у= хn Понятие корня стерениn Корни четной и нечетной степени Арифметический корень Свойства корней степени n Функция у=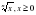 Контрольная работа № 2
Степень положительного числа.13ч. Степень с рациональным показателем Свойства степени с рациональным показателем Понятие предела последовательности Свойства пределов Бесконечно убывающая геометрическая прогрессия Число е Степень с иррациональным показателем Показательная функция Контрольная работа № 3 Логарифмы.6ч.
Понятие логарифма Свойства логарифмов Логарифмическая функция
Показательные и логарифмические уравнения и неравенства.11ч. Простейшие показательные уравнения Простейшие логарифмические уравнения Уравнения, сводящиеся к простейшим заменой неизвестного Простейшие показательные неравенства Простейшие логарифмические неравенства Неравенства, сводящиеся к простейшим заменой неизвестного Контрольная работа № 4
Синус, косинус угла.7ч. Понятие угла. Радианная мера угла Определение синуса и косинуса угла Основные формулы для sinх и cosх Арксинус Арккосинус Тангенс и котангенс угла. 6ч. Определение тангенса и котангенса угла Основные формулы для tgх и ctgх Арктангенс Арккотангенс Контрольная работа № 5 Формулы сложения.11ч. Косинус разности и косинус суммы двух углов. Синус суммы и синус разности двух углов. Формулы для дополнительных углов Сумма и разность синусов и косинусов Формулы для двойных и половинных углов Произведение синусов и косинусов Формулы для тангенсов Тригонометрические функции числового аргумента.9ч. Функция у= sinx Функция у= cosx Функция у= tgx Функция у= ctgx Контрольная работа № 6 Тригонометрические уравнения и неравенства.12ч. Простейшие тригонометрические уравнения Уравнения, сводящиеся к простейшим заменой неизвестного Применение основных тригонометрических формул для решения уравнений Однородные уравнения Простейшие неравенства для синуса и косинуса Простейшие неравенства для тангенса и котангенса Неравенства, сводящиеся к простейшим заменой неизвестного Введение вспомогательного угла Контрольная работа № 7
Элементы теории вероятностей.8ч. Понятие вероятности события Свойства вероятностей Относительная частота события Условная вероятность. Независимость событий Повторение. Итоговая контрольная работа Резерв
|
2 ч 2 ч 1 ч 1 ч 1 ч 1 ч 1 ч 1 ч 1 ч 1 ч
1 ч 2 ч 2 ч 2 ч 3 ч 3 ч 3 ч 1 ч 1 ч
1 ч 2 ч 1 ч 2 ч 2 ч 2 ч 1 ч 1 ч
1 ч 2 ч 2 ч 2 ч 1 ч 1 ч 1 ч 2 ч 1 ч
2 ч 3 ч 1 ч
1 ч 1 ч 2 ч 2 ч 2 ч 2 ч 1 ч
1 ч 1 ч 1 ч 2 ч 1 ч 1 ч
1 ч 2 ч 1 ч 1 ч 1 ч
2 ч 1 ч 2 ч 2 ч 2 ч 1 ч 1ч
2 ч 2 ч 2 ч 2 ч 1 ч
2 ч 2 ч 2 ч
1 ч 1 ч 1 ч 1 ч 1 ч 1 ч
3 ч 3 ч 1ч 1 ч 9 ч 2 ч 4 ч
|
Характеристика 10А класса Совершенно очевидно, что результативность осуществления учебной деятельности зависит от мотива. Большая часть обучающихся класса – это дети с высоким уровнем способностей и высокой мотивацией учения. Большинство из них приходят в школу учиться, им важно получить хорошие знания по предмету, так как они понимают, что от этого напрямую зависит их выбор дальнейшей профессии. Они в большинстве своем усваивают учебную программу на профильном уровне, с удовольствием и интересом выполняют задания повышенного уровня сложности. Ученики этого класса отличаются высокой организованностью, дисциплинированностью, ответственным отношением к выполнению учебных и домашних заданий. С учётом этого в содержание уроков включён материал повышенного уровня сложности, предлагаются дифференцированные задания как на этапе отработки зунов, так и на этапе контроля. В организации работы с этой группой обучающих учтен и тот факт, что они отличаются высоким уровнем самостоятельности в учебной деятельности и успешны в выполнении заданий творческого характера. Эти ребята уверены в себе, не боятся ошибиться и высказать свою точку зрения и предложить свой способ решения предложенных заданий. С учетом большого количества заинтересованных в изучении алгебры учеников на уроках, при проведении контрольных и самостоятельных работ и в домашних заданиях предлагаются задания, как базового, так профильного уровня.
Лишь небольшая часть детей пассивны, стесняются давать ответы в устной форме, грамотной математической речью не отличаются, такие дети боятся быть осмеянными, сделать что-то не так, выглядеть «слабыми» в глазах других. Для таких учащихся важно, чтобы в классе подчеркивалась их компетентность, обращалось внимание на то, что они умеет, могут. Им необходимо давать посильные задания для повышения их уровня самооценки.
На уроках высокая дисциплина, уважительное отношение к ответам одноклассников, частая работа в парах помогает им лучше освоить учебный материал и научить учиться. В целом, класс испытывает потребность в открытости, т.е. нуждается в поддержке, похвале, искренности педагога.
При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей их реализацией.
Образовательные технологии:
информационно-коммуникационные;
технология модульного обучения;
здоровьесберегающие;
использования в обучении игровых методов: ролевых, деловых и других видов обучающих игр;
проблемно-поисковый метод;
Признано, что основными технологиями развивающего обучения являются проблемно – поисковая, исследовательская технологии. Именно они позволяют создать такое образовательное пространство, в котором ученик является субъектом процесса обучения. Применение этих технологий обеспечивается строгим соблюдением такого дидактического принципа, как принцип систематичности и последовательности изложения материала.
Формы организации учебного процесса: индивидуальные, групповые,
индивидуально-групповые, фронтальные.
На уроках используются такие формы занятий как:
практические занятия;
тренинг;
консультация;
лекция.
Формы контроля: текущий и итоговый. Проводится в форме контрольных работ, рассчитанных на 40 минут, а итоговая на 90 минут, тестов и самостоятельных работ на 15 – 20 минут с дифференцированным оценивание.Текущий контроль проводится с целью проверки усвоения изучаемого и проверяемого программного материала; содержание определяются учителем с учетом степени сложности изучаемого материала, а также особенностей обучающихся класса. Итоговые контрольные работы проводятся:
после изучения наиболее значимых тем программы,
в конце учебной четверти,
в конце полугодия.
Основные типы учебных занятий:
урок изучения нового учебного материала;
урок закрепления и применения знаний;
урок обобщающего повторения и систематизации знаний;
урок контроля знаний и умений.
Основным типом урока является комбинированный.
Общеучебные умения, навыки и способы деятельности: В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:
- проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательствалогического обоснования выводов;
- различения доказанных и недоказанных утверждений;
- решения широкого класса задач из различных разделов курса, поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
- планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале;
- использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента;
- выполнения расчетов практического характера;
- построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни;
- проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
- самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
- самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Результаты обучения
Результаты обучения представлены в требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все выпускники, изучавшие курс математики напрофильному уровню, и достижение которых является обязательным условием положительной аттестации ученика за курс средней (полной) школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние две компоненты представлены отдельно по каждому из разделов, содержания.
Требования к уровню подготовки выпускников:
В результате изучения математики на профильном уровне ученик должен
Знать/понимать
существо понятия математического доказательства; приводить примеры доказательств;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.Находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна - две ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
- незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
- незнание наименований единиц измерения;
- неумение выделить в ответе главное;
- неумение применять знания, алгоритмы для решения задач;
- неумение делать выводы и обобщения;
- неумение читать и строить графики;
- неумение пользоваться первоисточниками, учебником и справочниками;
- потеря корня или сохранение постороннего корня;
- отбрасывание без объяснений одного из них.
УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
основная литература:
1. Программы общеобразовательных учреждений. Алгебра и начала математического анализа 10-11 классы.: Т. А. Бурмистрова. – М.: Просвещение, 2010.
С.М. Никольский, М.К. Потапов, и другие «Алгебра и начала математического анализа, 10 класс», базовый и профильный уровни. Просвещение, 2014г.
М.К. Потапов, А.В. Шевкин «Алгебра и начала математического анализа, 10 класс» – дидактические материалы, Просвещение, 2014г.
дополнительная литература:
Приложение к газете 1 сентября «Математика».
Сборники КИМов ЕГЭ.
Кодификатор элементов содержания математики для составления КИМов ЕГЭ 2015 года.
ЕГЭ 2015. Математика. Типовые тестовые задания; под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Экзамен», 2011.. (Серия «ЕГЭ 2015.Типовые тестовые задания»)
ЕГЭ 2015. Математика. Типовые задания ; под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Экзамен», 2015. (30 вариантов заданий + 800 заданий части 2 (С). Ответы и решения. Критерии оценок. Бланки ответов).
Лаппо, Л.Д. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие / Л.Д. Лаппо, М.А. Попов. — М.: Издательство «Экзамен», 2015 (Серия «ЕГЭ.Практикум»)
Методические рекомендации к учебникам математики для 10-11 классов, журнал «Математика в школе» №2-2005год;
Математика. Задачи М.И. Сканави с решениями. Сост. С.М. Марач, П.В. Полуносик. – Мн.: изд. В.М. Скакун, 1998г.
Тригонометрия. И.М. Гельфанд, С.М. Львовский, А.Л. Тоом. М.: МЦНМО, 2003г.
Математика. Повышенный уровень ЕГЭ-2015 (С1, С3). Тематические тесты. Уравнения, неравенства, системы./ под редакцией Ф.Ф. Лысенко, С,Ю. Кулабухова. – Ростов-на Дону: Легион-М, 2015г.
Перечень сайтов
http://www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)
http://www.center.fio.ru/som- методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
http://www.edu.ru- Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.
http://www.internet-scool.ru- сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ.
http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
http://www.fipi.ru - портал информационной поддержки ЕГЭ
http://mathege.ru. открытый банк заданий единого государственного экзамена по математике (ЕГЭ).
ttp://www.ege.edu.ru - Портал информационной поддержки проекта «Единый государственный экзамен»
http://www.moiege.ru - Портал для подготовки выпускников к госэкзаменам по 13 предметам. Интернет-среда предоставляет возможность пройти тесты с упражнениями, составленными на основе предыдущих экзаменов.
www.festival.1september.ru
МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Кабинет оборудован:
Компьютер
Медиа установка
Экран
Видео уроки
Алгебра 7-11 класс. Образовательная коллекция «1С-паблишинг»
Алгебра и начала анализа 10-11 класс. Просвещение-МЕДИА.
Алгебра и начала анализа итоговая аттестация выпускников. Просвещение-МЕДИА.
Математика. Экспресс подготовка к экзамену 9-11 класс. Новая школа
Интерактивный курс подготовки к ЕГЭ. Математика. Медиахауз
 N
N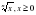
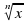 ,при х≥0
,при х≥0