| Сложение и вычитание натуральных чисел 33 ч |
| 20 | 1. Сложение натуральных чисел и его свойство | 1 |
| Актуализация знаний учащихся о сложении многозначных чисел. Свойства сложение натуральных чисел. Применение свойств сложения при устных вычислениях. Работа с текстовыми задачами. Повторение разрядных составов числа и правила его замены суммой разрядных слагаемых. Повторение понятия периметра треугольника | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам
| Числа, которые складывают, называют слагаемыми. Сумма - число получающееся при сложении чисел. Сумма чисел не изменяется при перестановки слагаемых. Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме – второе слагаемое. От прибавления нуля число не изменяется. Периметр - сумма длин сторон многоугольника | Слагаемое, сумма, переместительное свойство, сочетательное свойство, периметр |
| 21 | 2. Сложение натуральных чисел и его свойство | 1 |
| КУ |
| 22 | 3. Сложение натуральных чисел и его свойство | 1 |
| УПЗУ |
| 23 | 4. Сложение натуральных чисел и его свойство | 1 |
| УПЗУ |
| 24 | 5. Вычитание натуральных чисел и его свойство | 1 |
| Систематизация знаний учащихся о действии вычитания, полученные в начальной школе. Повторение свойства вычитания суммы из числа и числа из суммы, применение этих свойств при вычислениях. Работа над текстовыми задачами | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Вычитание - действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое. Число из которого вычитают, называют уменьшаемым, чисто, которое вычитают, -вычитаемым. Разность - результат вычитания. Разность двух чисел показывает, на сколько первое число больше второго. Для того чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности - второе слагаемое. Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое | Вычитание, уменьшаемое, вычитаемое, разность, свойство вычитания суммы из числа, свойство вычитания числа из суммы, вычесть, отнять |
| 25 | 6. Вычитание натуральных чисел и его свойство | 1 |
| КУ |
| 26 | 7. Вычитание натуральных чисел и его свойство | 1 |
| УПЗУ |
| 27 | 8. Вычитание натуральных чисел и его свойство | 1 |
| УПЗУ |
| 28 | 9. Вычитание натуральных чисел и его свойство | 1 |
| УПЗУ |
| 29 | 10. Вычитание натуральных чисел и его свойство | 1 |
| УОИСЗ |
| 30 | 11. Числовые и буквенные выражения | 1 |
| Понятие буквенного выражения, записывание и чтение буквенных выражений. Записывание решение задач способом составления числового или буквенного выражения. Решение текстовых задач | УИНМ | При решении задач записывают действия, эти полученные записи, называют числовыми выражениями. Буквенные выражения - выражения, содержащие буквы. Значение буквы - число, которым заменяют букву | Числовое выражение, буквенное выражение, значение буквы, значение выражения |
| 31 | 12. Числовые и буквенные выражения | 1 |
| КУ |
| 32 | 13.Числовые и буквенные выражения | 1 |
| КУ |
| 33 | 14. Числовые и буквенные выражения | 1 |
| УПЗУ |
| 34 | 15. Буквенная запись свойств сложения и вычитания | 1 |
| Ознакомление учащихся с буквенной записью свойств сложения и вычитания. Совершенствование вычислительных навыков учащихся | УИНМ | В переместительном и сочетательном свойствах сложения буквы могут принимать любые натуральные значения и значение 0. Свойство вычитания суммы из числа записывают при условии, что сумма чисел меньше или равна уменьшаемого. Свойство вычитания числа из суммы записывают при условии, что вычитаемое меньше или равно уменьшаемого | Уменьшаемое, вычитание, разность, слагаемое. сумма, свойство сложения, свойство вычитания, натуральные числа |
| 35 | 16. Буквенная запись свойств сложения и вычитания | 1 |
| КУ |
| 36 | 17. Упрощение выражения | 1 |
| Упрощение выражения с опорой на свойства сложения и вычитания. Совершенствование вычислительных навыков учащихся. Решение текстовых задач | КУ |
| 37 | 18. Упрощение выражения | 1 |
| КУ |
| 38 | 19. Упрощение выражения | 1 |
| КУ |
| 39 | 20. Упрощение выражения | 1 |
| УПЗУ |
| 40 | 21. Подготовка к контрольной работе | 1 |
| Проверка умений выполнять сложение и вычитание натуральных чисел. Решение текстовых задач на сложение и вычитание | УЗЗ | См. урок № 1 - № 20 темы «Сложение и вычитание натуральных чисел»
См. урок № 1 - № 20 темы «Сложение и вычитание натуральных чисел» |
| 41 | 22. Контрольная работа № 2 по теме «Сложение и вычитание натуральных чисел» | 1 |
|
| КР |
| 42 | 23. Уравнения. Решение уравнений | 1 |
| Актуализация знания учащихся об уравнениях, полученные в начальной школе. Понятие корня уравнения. Ознакомление учащихся с алгебраическим способом решения задач. Формирование умений решать уравнения и задачи способом составления уравнений. | УИНМ | Уравнением называют равенство, содержащее букву, значение которой надо найти. Корень уравнения - это значение буквы, при котором из уравнения получается верное числовое равенство. Решить уравнение - значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня). Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
| Уравнение, равенство, значение, корни уравнения, неизвестное слагаемое, неизвестное уменьшаемое, неизвестное вычитаемое, сумма, разность |
| 43 | 24. Уравнения. Решение уравнений | 1 |
| КУ |
| 44 | 25. Уравнения. Решение уравнений | 1 |
| КУ |
| 45 | 26. Решение задач при помощи уравнений | 1 |
| Формирование умений решать задачи способом при помощи уравнений. Совершенствовать вычислительные навыки учащихся | КУ |
| 46 | 27. Решение задач при помощи уравнений | 1 |
| КУ |
| 47 | 28. Решение задач при помощи уравнений | 1 |
| УПЗУ |
| 48 | 29. Решение задач при помощи уравнений | 1 |
| Решение уравнений и задач. Составление уравнения по задачам | УПЗУ |
| 49 | 30. Решение задач при помощи уравнений | 1 |
| Решение уравнений и задач. Составление уравнения по задачам | УПЗУ |
| 50 | 31. Решение задач при помощи уравнений | 1 |
| Решение уравнений. Продолжение работы по обучению учащихся алгебраическому способу решения задач | УЗЗ |
| 51 | 32. Подготовка к контрольной работе | 1 |
| Повторение пройденного материала. Подготовка к контрольной работе | УЗЗ |
| См. урок № 13 - № 31 темы «Сложение и вычитание натуральных чисел» | См. урок № 13 - № 31 темы «Сложение и вычитание натуральных чисел» |
| 52 | 33. Контрольная работа № 3 по теме «Числовые и буквенные выражения. Уравнение» | 1 |
| Контрольная работа № 3 по теме «Числовые и буквенные выражения. Уравнение» | КР |
| Умножение и деление натуральных чисел 30 ч |
| 53 | 1. Умножение натурального числа и его свойства | 1 |
| Актуализация знаний учащихся о действии умножения, полученные в начальной школе. Работа над текстовыми задачами | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Умножить число m на натуральное число n- значит найти сумму n слагаемых, каждое из которых равно m. Выражение m ∙ n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями. Произведение двух чисел не изменяется при перестановки множителей. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель | Натуральное число, сумма, множитель, произведение, переместительное свойство умножения, сочетательное свойство умножения, скобка, знак, первый множитель, второй множитель |
| 54 | 2. Умножение натурального числа и его свойства | 1 |
| КУ |
| 55 | 3. Умножение натурального числа и его
свойства | 1 |
| Совершенствование навыков умножения натуральных чисел. Использование в устных вычислениях свойства умножения. Работа над текстовыми задачами. Рациональный прием вычислений. Чтение и запись выражения, содержащие действие умножения. Совершенствование вычислительных навыков учащихся. Ознакомления с приемом умножения двухзначного числа на 11 | КУ |
| 56 | 4. Умножение натурального числа и его свойства | 1 |
| КУ |
| 57 | 5. Умножение натурального числа и его свойства | 1 |
| КУ |
| 58 | 6. Умножение натурального числа и его свойства | 1 |
| УПЗУ |
| 59 | 7. Умножение натурального числа и его свойства | 1 |
| УЗЗ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
|
| 60 | 8. Вынесение общего множителя за скобки | 1 |
| Вынесение общего множителя за скобки. Совершенствование вычислительных навыков учащихся. Работа над текстовыми задачами | КУ |
| 61 | 9. Вынесение общего множителя за скобки | 1 |
| КУ |
| 62 | 10. Вынесение общего множителя за скобки | 1 |
| КУ |
| 63 | 11. Деление натуральных чисел | 1 |
| Актуализация знаний учащихся о действии деления. Повторение алгоритма письменного деления. Работа над текстовыми задачами | УИНМ | Деление - это действие, с помощью которого по произведению и одному из множителей находят другой множитель. Число которое делят называется делимым. Число на которое делят, называют делителем. Результат деления называют частным. Частное показывает, во сколько раз делимое больше, чем делитель. Ни одно число нельзя делить на нуль. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель. Чтобы найти неизвестное делимое, надо частное умножить на делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное | Деление, делимое, делитель, произведение, множитель, частное, нуль, неизвестный множитель, неизвестное делимое, неизвестный делитель
|
| 64 | 12. Деление натуральных чисел | 1 |
| КУ |
| 65 | 13. Деление натуральных чисел | 1 |
| КУ |
| 66 | 14. Деление натуральных чисел | 1 |
| Формирование умения выполнять деление в столбик и проверку деления. Чтение и записывание выражения, содержащие действия деления | КУ |
| 67 | 15. Деление натуральных чисел | 1 |
| УПЗУ |
| 68 | 16. Деление натуральных чисел | 1 |
| УПЗУ |
| 69 | 17. Деление натуральных чисел | 1 |
| Совершенствование вычислительных навыков учащихся. Рассмотрение случаев деления с нулями в частном. Работа над текстовыми задачами | УПЗУ |
| 70 | 18. Деление с остатком |
|
| Повторение деления с остатком. Выполнение деление с остатком | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Деление одного натурального числа на другое нацело не всегда возможно, иногда получается деление с остатком. Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток | Деление с остатком, делимое, делитель, неполное частное, остаток, без остатка, нацело |
| 71 | 19. Деление с остатком |
|
| Формирование навыков выполнения деления с остатком. Работа над текстовыми задачами | КУ |
| 72 | 20. Порядок выполнения действий | 1 |
| Порядок выполнения действий. Действие первой ступени и действие второй ступени. Решение текстовых задач | КУ | Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку с лева на право. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2) | Действия первой ступени, действия второй ступени, скобки, выражение, сложение, вычитание, умножение, деление |
| 73 | 21. Порядок выполнения действий | 1 |
| КУ |
| 74 | 22. Задачи на все действия с натуральными числами | 1 |
| Повторение обозначения натуральных чисел. Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Умножение и деление натуральных чисел. Решение текстовых задач. Решение уравнений и составление уравнения по задачам | КУ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| См. урок № 1 - № 20 тем: «Натуральные числа и шкалы», «Сложение и вычитание натуральных чисел», «Умножение и деление натуральных чисел» | См. урок № 1 - № 20 тем: «Натуральные числа и шкалы», «Сложение и вычитание натуральных чисел», «Умножение и деление натуральных чисел» |
| 75 | 23. Задачи на все действия с натуральными числами | 1 |
| КУ |
| 76 | 24. Подготовка к контрольной работе | 1 |
| Проверка формирования вычислительных навыков, проверка умения решать уравнения и задачи способом составления уравнений | УЗЗ |
| 77 | 25. Контрольная работа № 4 на первое полугодие | 1 |
| КР |
| 78 | 26. Задачи на все действия с натуральными числами | 1 |
| Повторение обозначения натуральных чисел. Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Умножение и деление натуральных чисел. Решение текстовых задач. Решение уравнений и составление уравнения по задачам | КУ | См. урок № 1 - № 20 тем: «Натуральные числа и шкалы», «Сложение и вычитание натуральных чисел», «Умножение и деление натуральных чисел» | См. урок № 1 - № 20 тем: «Натуральные числа и шкалы», «Сложение и вычитание натуральных чисел», «Умножение и деление натуральных чисел» |
| 79 | 27. Задачи на все действия с натуральными числами | 1 |
| КУ |
| 80 | 28. Квадрат и куб числа | 1 |
| Ознакомление учащихся с возведением числа в степень. Понятие квадрата и куба числа. Работа над текстовыми задачами | УИНМ |
| Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Произведение n ∙ n ∙ n называют кубом числа n и обозначают n3 (читают: «эн в кубе»). Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий | Степень числа, основание, показатель степени, квадрат числа, куб числа |
| 81 | 29. Квадрат и куб числа | 1 |
| КУ |
| 82 | 30. Квадрат и куб числа | 1 |
| Формирование умения выполнять возведение числа в степень. Совершенствовать вычислительные навыки учащихся | КУ |
| Площадь и объем 17 ч |
| 83 | 1. Формулы. Вычисления по формулам | 1 |
| Понятие «формула». Формула нахождения пути , если известно скорость и время выполнение вычислений по формулам. Работа над текстовыми задачами | УИНМ | Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Запись какого-нибудь правила с помощью букв называют формулой | Формула, скорость, время, расстояние |
| 84 | 2. Формулы. Вычисления по формулам | 1 |
| КУ |
| 85 | 3. Формулы. Вычисления по формулам | 1 |
| КУ |
| 86 | 4. Формулы. Вычисления по формулам | 1 |
| Работа над формированием вычисления по формулам, совершенствование вычислительных навыков | УОИСЗ | Запись какого-нибудь правила с помощью букв называют формулой | Формула, скорость, время, расстояние |
| 87 | 5. Формулы. Вычисления по формулам | 1 |
| УОИСЗ |
| 88 | 6. Формулы. Вычисления по формулам | 1 |
| УОИСЗ |
| 89 | 7. Площадь. Прямоугольник. Площадь прямоугольника | 1 |
| Площади прямоугольника и квадрата, формулы их площадей. Равные фигуры | УИНМ | Чтобы найти площадь прямоугольника, надо умножить его длину на ширину. Площадь всей фигуры равна сумме площадей ее частей. Площади равных фигур равны. Их периметры тоже равны | Площадь, формула, прямоугольник, квадратный сантиметр, периметр |
| 90 | 8. Площадь прямоугольника | 1 |
| КУ |
| 91 | 9. Площадь прямоугольника | 1 |
| КУ |
| 92 | 10. Единицы измерения площади | 1 |
| Единицы измерения площади . Выражать одни единицы измерения площади через другие | УИНМ | Если длина и ширина прямоугольника выражены в метрах, то его площадь выражается в квадратных метрах. Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах | Длина, ширина, метр, квадратный метр, квадратный миллиметр, квадратный сантиметр, квадратный дециметр, ар |
| 93 | 11. Прямоугольный параллелепипед | 1 |
| Распознавание на чертежах, рисунках, в окружающем мире геометрические фигуры, имеющие форму параллелепипеда, изображать параллелепипед. Верно использовать в речи термины: параллелепипед, куб, ребра, грани и вершины параллелепипеда | УИНМ | Противоположные грани прямоугольного параллелепипеда равны. Куб - это прямоугольный параллелепипед, у которого все измерения одинаковы | Параллелепипед, куб, грани, ребра, длина, ширина, высота |
| 94 | 12. Прямоугольный параллелепипед | 1 |
| КУ |
| 95 | 13. Прямоугольный параллелепипед | 1 |
| УОИСЗ |
| 96 | 14. Объем. Объем прямоугольного параллелепипеда | 1 |
| Формулы объёма прямоугольного параллелепипеда, куба. Определение объёма фигуры по количеству кубических сантиметров, уложенных в ней. Вычисление объёма куба и прямоугольного параллелепипеда, используя формулы | КУ | Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту | Объем, прямоугольный параллелепипед, длина, ширина, высота, куб |
| 97 | 15. Объем. Объем прямоугольного параллелепипеда | 1 |
| УОИСЗ |
|
| 98 | 16. Подготовка к контрольной работе | 1 |
| Повторение пройденного материала. Подготовка к контрольной работе. Решение задач | УЗЗ | См. урок № 1 - № 15 темы «Площадь и объем» | См. урок № 1 - № 15 темы «Площадь и объем» |
| 99 | 17. Контрольная работа № 5 по теме «Площадь и объем» | 1 |
| Контрольная работа № 5 по теме «Площадь и объем» | КР | См. урок № 1 - № 15 темы «Площадь и объем» | См. урок № 1 - № 15 темы «Площадь и объем» |
| Дробные числа. Обыкновенные дроби 32 ч |
| 100 | 1. Окружность и круг | 1 |
| Распознавание на рисунках, в окружающем мире геометрические фигуры, имеющие форму окружности, круга. Пример аналогов окружности, круга в окружающем мире. Изображение окружность с использованием циркуля. Построение окружности с заданным центром и радиусом. Решение задач практической направленности | УИНМ | Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам | Круг - это та часть плоскости, которая лежит внутри окружности. Все точки окружности одинаково удалены от ее центра. Диаметр делит круг на два полукруга, а окружность - на две полуокружности | Круг, окружность, центр, радиус, диаметр, полукруг, полуокружность, дуга |
| 101 | 2. Окружность и круг | 1 |
| КУ |
| 102 | 3. Обыкновенные дроби | 1 |
| Обыкновенные дроби. Числитель и знаменатель. Изображение обыкновенной дроби на координатном луче. Чтение и запись дробей и выражений, содержащих обыкновенные дроби | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
|
| 103 | 4. Доли. Обыкновенные дроби | 1 |
| КУ | Долю 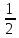 называют половиной, называют половиной, 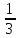 - третью, а - третью, а 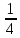 - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято | Доля, половина, треть, четверть, числитель, знаменатель |
| 104 | 5. Доли. Обыкновенные дроби | 1 |
| КУ |
| 105 | 6. Доли. Обыкновенные дроби | 1 |
| КУ |
| 106 | 7. Доли. Обыкновенные дроби | 1 |
| Доли. Обыкновенные дроби. Числитель и знаменатель. Решение задач на нахождение дроби от числа и нахождения числа по его дроби | КУ |
| 107 | 8. Доли. Обыкновенные дроби | 1 |
| УОИСЗ | Долю 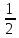 называют половиной, называют половиной, 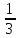 - третью, а - третью, а 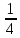 - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято | Доля, половина, треть, четверть, числитель, знаменатель |
| 108 | 9. Доли. Обыкновенные дроби | 1 |
| УОИСЗ |
| 109 | 10. Доли. Обыкновенные дроби | 1 |
| УОИСЗ |
| 110 | 11. Доли. Обыкновенные дроби | 1 |
| Доли. Обыкновенные дроби. Числитель и знаменатель. Чтение и запись дробей и выражений, содержащих обыкновенные дроби. Анализ текста задачи, извлекая необходимую информацию, решение задач | УОИСЗ |
| 111 | 12. Доли. Обыкновенные дроби | 1 |
| УОИСЗ | Долю 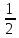 называют половиной, называют половиной, 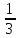 - третью, а - третью, а 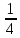 - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято | Доля, половина, треть, четверть, числитель, знаменатель |
| 112 | 13. Доли. Обыкновенные дроби | 1 |
| УОИСЗ |
| 113 | 14. Доли. Обыкновенные дроби | 1 |
| УОИСЗ |
| 114 | 15. Доли. Обыкновенные дроби | 1 |
| УЗЗ |
| 115 | 16. Сравнение обыкновенных дробей | 1 |
| Сравнение дробей с одинаковым знаменателем. Сравнение обыкновенных дробей, с помощью координатного луча и пользуясь правилом. Решение текстовых задач арифметическими способами | УИНМ | Две равные дроби обозначают одно и то же дробное число. Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель | Дробь, числитель, знаменатель |
| 116 | 17. Сравнение обыкновенных дробей | 1 |
| КУ |
| 117 | 18. Сравнение обыкновенных дробей | 1 |
| КУ |
| 118 | 19. Правильные и неправильные дроби | 1 |
| Правильные и неправильные обыкновенные дроби. Изображение на координатном луче правильные и неправильные дроби. Сравнение правильной и неправильной дроби с единицей и друг с другом. Анализ текста задачи. Решение задач | КУ | Дробь, в которой числитель меньше знаменателя, называют правильной дробью. Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью. Правильна дробь меньше единицы, а неправильная дробь больше или равна единице | Дробь, правильная дробь, неправильная дробь, числитель, знаменатель |
| 119 | 20. Правильные и неправильные дроби | 1 |
| КУ |
| 120 | 21. Правильные и неправильные дроби
| 1 |
| УЗЗ |
| 121 | 22. Сложение и вычитание дробей с одинаковыми знаменателями | 1 |
| Сложение и вычитание дробей с одинаковыми знаменателями. Решение текстовых задач арифметическими способами вычислений, анализ текста задач | УИНМ | При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же. При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же |
|
| 122 | 23. Сложение и вычитание дробей с одинаковыми знаменателями
| 1 |
| КУ | Дробь, числитель, знаменатель, сложение дробей, вычитание дробей |
| 123 | 24. Деление и дробь | 1 |
| Деление и дроби. Представление частного в виде дроби. Свойство деления суммы на число | УИНМ | Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные | Дробь, натуральное число, числитель, знаменатель |
| 124 | 25. Деление и дробь
| 1 |
| КУ |
| 125 | 26. Смешанные числа | 1 |
| Смешанные числа. Целая и дробная часть числа. Понятие «Смешанное число». Преобразование неправильной дроби в смешанное число и смешанного числа в неправильную дробь. Изображение точками на координатном луче правильные и неправильные дроби | УИНМ | Запись числа, содержащую целую и дробную части, называют смешанной. Смешанное число можно представить в виде неправильной дроби | Целая часть, дробная часть, смешанное число, правильная дробь, неправильная дробь |
| 126 | 27. Смешанные числа | 1 |
| КУ |
| 127 | 28. Смешанные числа | 1 |
| УЗЗ |
| 128 | 29. Сложение и вычитание смешанных чисел | 1 |
| Правила сложения и вычитания смешанных чисел. Выполнение сложения и вычитания смешанных чисел, у которых дробная часть первого меньше дробной части второго или отсутствует вовсе. Решение текстовых задач
| УИНМ | При сложении и вычитании чисел в смешанной записи целые части складывают или вычитают отдельно, а дробные - отдельно | Сложение, вычитание, смешанное число, целое число, дробь |
| 129 | 30. Сложение и вычитание смешанных чисел | 1 |
| КУ |
| 130 | 31. Подготовка к контрольной работе | 1 |
| Повторение пройденного материала. Подготовка к контрольной работе | УЗЗ |
| См. урок № 1 - 30 темы «Дробные числа. Обыкновенные дроби» | См. урок № 1 - 30 темы «Дробные числа. Обыкновенные дроби» |
| 131 | 32. Контрольная работа № 6 по теме «Обыкновенные дроби. Правильные и неправильные дроби» | 1 |
| Контрольная работа № 6 по теме «Обыкновенные дроби. Правильные и неправильные дроби» | КР |
| Десятичные дроби 27 ч |
| 132 | 1. Десятичная запись дробных чисел | 1 |
| Десятичная дробь, целая и дробная части числа. Понятие «десятичная дробь». Чтение, запись десятичной дроби. Представление обыкновенной дроби в виде десятичной и наоборот
| УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Любое число, знаменатель дробной части которого выражается единицей с одним или несколькими нулями, можно представить в виде десятичной записи, или, как говорят иначе, в виде десятичной дроби. Числа со знаменателями 10, 100, 1000 и т. д. записывают без знаменателя, сначала пишут целую часть, а потом числитель дробной части, целую часть отделяют от дробной части запятой | Знаменатель, десятичная дробь, запятая, целая часть, числитель |
| 133 | 2. Десятичная запись дробных чисел | 1 |
| КУ |
| 134 | 3. Десятичная запись дробных чисел | 1 |
| КУ |
| 135 | 4. Десятичная запись дробных чисел | 1 |
| УОИСЗ |
| 136 | 5. Десятичная запись дробных чисел | 1 |
| УОИСЗ | Знаменатель, десятичная дробь, запятая, целая часть, числитель |
| 137 | 6. Десятичная запись дробных чисел | 1 |
| УЗЗ |
| 138 | 7. Сравнение десятичных дробей | 1 |
| Сравнение десятичных дробей. Алгоритмом сравнения десятичных дробей. Изображение десятичной дроби на координатном луче. Запись десятичных дробей в порядке возрастания или убывания | УИНМ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски, контрольная работа | Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнивать получившиеся натуральные числа. Равные десятичные дроби изображаются на координатном луче одной и той же точкой | Десятичная дробь, нуль, координатный луч |
| 139 | 8. Сравнение десятичных дробей | 1 |
| КУ |
| 140 | 9. Сравнение десятичных дробей | 1 |
| УОИСЗ |
| 141 | 10. Сравнение десятичных дробей | 1 |
| УОИСЗ |
| 142 | 11. Сложение и вычитание десятичных дробей | 1 |
| Сложение и вычитание десятичных дробей. Приёмы выполнения сложения и вычитания десятичных дробей. Представление десятичных дробей в виде суммы разрядных слагаемых. Решение текстовых задач | УИНМ | Что бы сложить (вычесть) десятичные дроби, нужно: уравнять в этих дробях количество знаков после запятой, записать их друг под другом так, чтобы запятая была записана под запятой, выполнить сложение (вычитание), не обращая внимания на запятую, поставить в ответе запятую под запятой в данных дробях | Десятичная дробь, нуль, разложение числа по разрядам, высший разряд, низший разряд, сложение, вычитание |
| 143 | 12. Сложение и вычитание десятичных дробей | 1 |
| КУ |
| 144 | 13. Сложение и вычитание десятичных дробей | 1 |
| КУ |
| 145 | 14. Сложение и вычитание десятичных дробей | 1 |
| Сложение и вычитание десятичные дробей. Запись переместительного и сочетательного законов сложения при помощи букв и проверка их при заданных значениях букв. Решение задач на движение | КУ |
| 146 | 15. Сложение и вычитание десятичных дробей | 1 |
| КУ |
| 147 | 16. Сложение и вычитание десятичных дробей | 1 |
| КУ |
| 148 | 17.Сложение и вычитание десятичных дробей | 1 |
| КУ |
| 149 | 18. Сложение и вычитание десятичных дробей | 1 |
| Представление десятичных дробей в виде суммы разрядных слагаемых.Сложение и вычитание десятичных дробей. Сравнивание десятичных дробей. Решение текстовых задач | УОИСЗ |
| 150 | 19. Сложение и вычитание десятичных дробей | 1 |
| УОИСЗ |
| 151 | 20. Приближенные значения чисел. Округление чисел | 1 | 24.04 | Приближенные значения чисел с недостатком и избытком. Округление чисел. Понятие «приближённое значение числа». Алгоритм округления чисел. Решение текстовых задач | УИНМ | Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых. Если аb, то а называют приближенным значением числа х с недостатком, а b - приближенным значением х с избытком | Замена числа, приближенное значение, округление Замена числа, приближенное значение, округление |
| 152 | 21. Приближенные значения чисел. Округление чисел | 1 | 24.04 | КУ |
| 153 | 22. Приближенные значения чисел. Округление чисел | 1 | 28.04 | КУ |
| 154 | 23. Приближенные значения чисел. Округление чисел | 1 | 29.04 | УОИСЗ |
| 155 | 24. Приближенные значения чисел. Округление чисел | 1 | 30.04 | УОИСЗ |
| 156 | 25. Приближенные значения чисел. Округление чисел | 1 | 30.04 | УОИСЗ |
| 157 | 26. Подготовка к контрольной работе | 1 | 7.05 | Повторение пройденного материала. Подготовка к контрольной работе | УЗЗ | См. урок № 1 - № 25 темы «Десятичные дроби» | См. урок № 1 - № 25 темы «Десятичные дроби» |
| 158 | 27. Контрольная работа № 7 по теме «Десятичные дроби» | 1 | 7.05 | Контрольная работа № 7 по теме «Десятичные дроби» | КР | См. урок № 1 - № 25 темы «Десятичные дроби» | См. урок № 1 - № 25 темы «Десятичные дроби» |
| Обобщающее повторение 12 ч |
| 159 | 1. Повторение | 1 |
| Чтение и запись натуральных чисел, определение значимости числа, сравнивание и упорядочивания их. Запись с помощью букв свойства сложения, вычитания и умножения. Выполнение деления с остатком | УОИСЗ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Однозначное число - натуральное число, состоящее из одного знака. Двузначное число - состоящее из двух знаков. Многозначное число - натуральное число, состоящее из двух и более знаков. Класс: единицы, тысячи, миллионы, миллиарды. Разряд: единицы, десятки, сотни | Натуральный ряд, натуральное число, многозначное число, класс, единица, тысяча, миллион, миллиард, разряд, десятки, сотни, разряд единиц |
| 160 | 2. Повторение | 1 |
| Сложение, вычитание, умножение и деление натуральных чисел. Нахождение значения числовых и буквенных выражений | УОИСЗ | Сумма - число получающееся при сложении чисел. Сумма чисел не изменяется при перестановки слагаемых. Вычитание - действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое. Умножить число m на натуральное число n- значит найти сумму n слагаемых, каждое из которых равно m. Деление - это действие, с помощью которого по произведению и одному из множителей находят другой множитель. | Слагаемое, вычитаемое, уменьшаемое, разность, сумма, переместительное свойство, сочетательное свойство, периметр, умножение, множитель, деление, делитель, частное, произведение |
| 161 | 3. Повторение | 1 |
| Нахождение значения числовых выражений, содержащих несколько действий. Решение задачи на составление буквенных выражений. Упрощение буквенных выражений с помощью свойств сложения, вычитания и умножения | УЗЗ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Буквенные выражения - выражения, содержащие буквы. Значение буквы - число, которым заменяют букву | Числовое выражение, буквенное выражение, значение буквы, значение выражения |
| 162 | 4. Повторение | 1 |
| Нахождение значения числовых выражений, содержащих несколько действий. Решение задач на составление буквенных выражений. Упрощение буквенных выражений с помощью свойств сложения, вычитания и умножения | УОИСЗ | При решении задач записывают действия, эти полученные записи, называют числовыми выражениями. | Числовое выражение, буквенное выражение, значение буквы, значение выражения |
| 163 | 5. Повторение | 1 |
| УЗЗ |
| 164 | 6. Итоговая контрольная работа | 1 |
| Итоговая контрольная работа | КР | См. урок № 1 - 157 тем «Натуральные числа и шкалы», «Сложение и вычитание натуральных чисел», «Умножение и деление натуральных чисел», «Площадь и объем», «Дробные числа. Обыкновенные дроби», «Десятичные дроби» |
| 165 | 7. Повторение | 1 |
| Решение задач на нахождение площадей и объёмов | УОИСЗ |
Устный опрос, работа с учебником, самостоятельная работа, математический диктант, фронтальная работа с классом, индивидуальная работа по карточкам, проверка домашнего задания, работа у доски
| Чтобы найти площадь прямоугольника, надо умножить его длину на ширину. Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту | Объем, прямоугольный параллелепипед, длина, ширина, высота, куб |
| 166 | 8. Повторение | 1 |
| Выполнение сложения и вычитания смешанных чисел. Решение текстовых задач арифметическими способами вычислений | УОИСЗ | Запись числа, содержащую целую и дробную части, называют смешанной. Смешанное число можно представить в виде неправильной дроби | Целая часть, дробная часть, смешанное число, правильная дробь, неправильная дробь |
| 167 | 9. Повторение | 1 |
| УЗЗ |
| 168 | 10. Повторение | 1 |
| УЗЗ |
| 169 | 11. Повторение | 1 |
| Сложение и вычитание десятичных дробей. Решение примеров в несколько действий. Решение уравнений с десятичными дробями | УОИСЗ | Что бы сложить (вычесть) десятичные дроби, нужно: уравнять в этих дробях количество знаков после запятой, записать их друг под другом так, чтобы запятая была записана под запятой, выполнить сложение (вычитание), не обращая внимания на запятую, поставить в ответе запятую под запятой в данных дробях | Десятичная дробь, нуль, разложение числа по разрядам, высший разряд, низший разряд, сложение, вычитание |
| 170 | 12. Повторение | 1 |
| УОИСЗ |
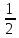 называют половиной,
называют половиной, 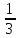 - третью, а
- третью, а 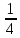 - четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято
- четвертью. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято



















