Интерактивное пособие для подготовки учащихся к ОГЭ (раздел «Геометрия»)
Задание 16
«Четырехугольники»
Учитель математики МОУ СОШ №3 г. Хвалынска
Грибанова Татьяна Алексеевна
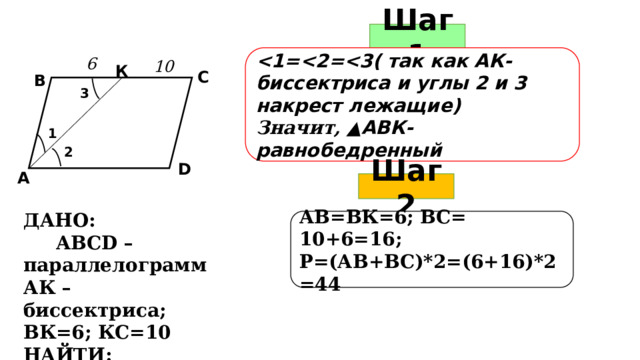
Шаг 1
Значит, ▲АВК-равнобедренный
6
10
К
С
В
3
1
2
D
А
Шаг 2
ДАНО:
АВСD –параллелограмм
АК – биссектриса;
ВК=6; КС=10
НАЙТИ: периметр
АВ=ВК=6; ВС= 10+6=16;
Р=(АВ+ВС)*2=(6+16)*2=44
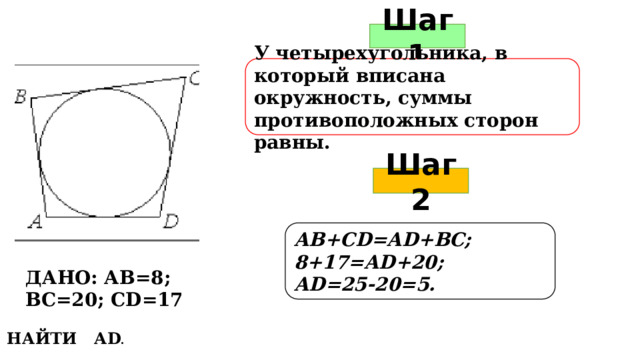
Шаг 1
У четырехугольника, в который вписана окружность, суммы противоположных сторон равны.
Шаг 2
АВ+СD=АD+ВС; 8+17=АD+20;
АD=25-20=5.
ДАНО: АВ=8; ВС=20; СD=17
НАЙТИ АD .
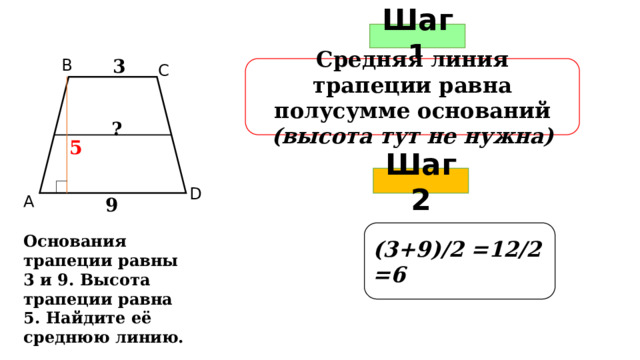
Шаг 1
3
В
С
Средняя линия трапеции равна полусумме оснований (высота тут не нужна)
?
5
Шаг 2
D
А
9
(3+9)/2 =12/2 =6
Основания трапеции равны 3 и 9. Высота трапеции равна 5. Найдите её среднюю линию.
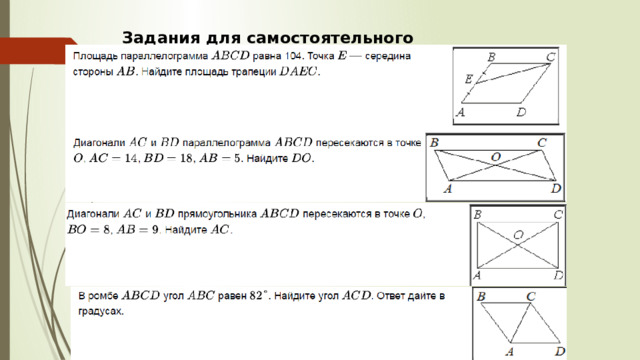
Задания для самостоятельного решения
1)
2)
3)
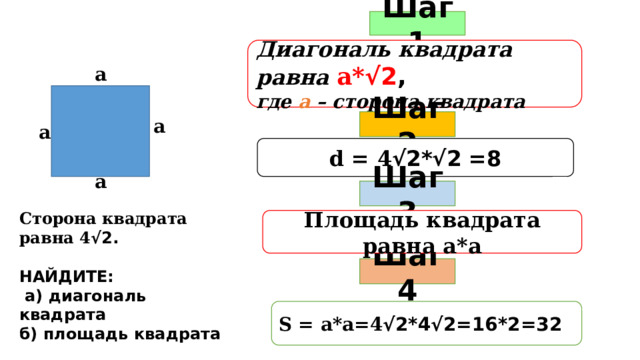
Шаг 1
Диагональ квадрата равна а* √2 ,
где а – сторона квадрата
а
Шаг 2
а
а
d = 4 √2*√2 =8
а
Шаг 3
Сторона квадрата равна 4 √2.
НАЙДИТЕ:
а) диагональ квадрата
б) площадь квадрата
Площадь квадрата равна а*а
Шаг 4
S = a*a=4 √2*4√2=16*2=32
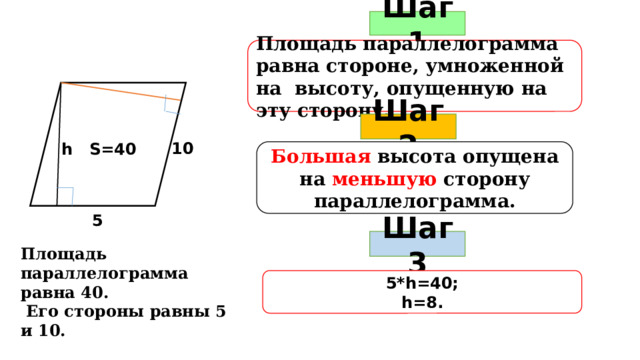
Шаг 1
Площадь параллелограмма равна стороне, умноженной на высоту, опущенную на эту сторону.
Шаг 2
10
S=40
h
Большая высота опущена на меньшую сторону параллелограмма.
5
Шаг 3
Площадь параллелограмма равна 40.
Его стороны равны 5 и 10.
Найдите его большую высоту.
5*h=40;
h=8.
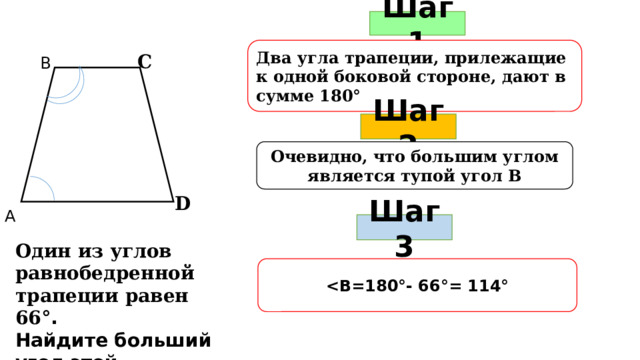
Шаг 1
Два угла трапеции, прилежащие к одной боковой стороне, дают в сумме 180 °
С
В
Шаг 2
?
Очевидно, что большим углом является тупой угол В
D
А
Шаг 3
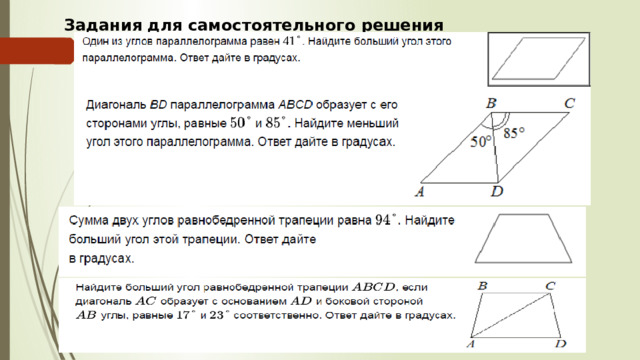
Один из углов равнобедренной трапеции равен 66 °.
Найдите больший угол этой трапеции.
Задания для самостоятельного решения
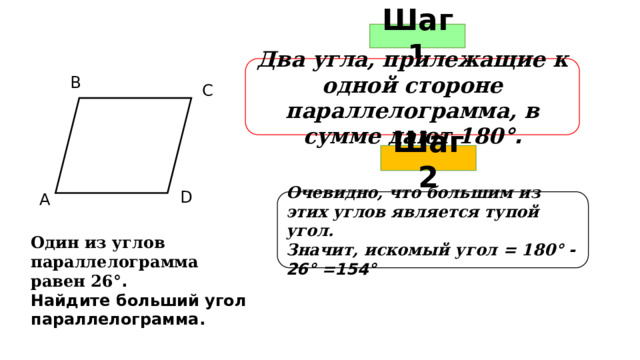
Шаг 1
Два угла, прилежащие к одной стороне параллелограмма, в сумме дают 180 °.
В
С
Шаг 2
D
А
Очевидно, что большим из этих углов является тупой угол.
Значит, искомый угол = 180 ° - 26° =154°
Один из углов параллелограмма равен 26 °.
Найдите больший угол параллелограмма.
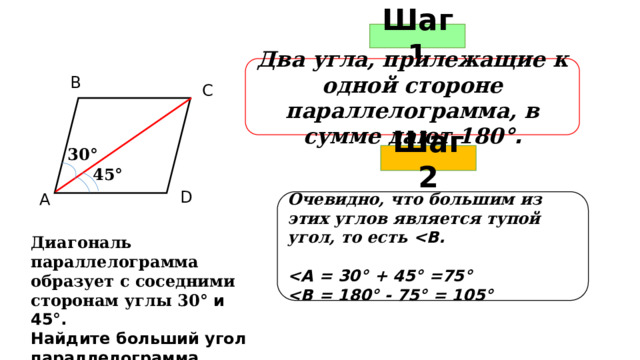
Шаг 1
Два угла, прилежащие к одной стороне параллелограмма, в сумме дают 180 °.
В
С
30 °
Шаг 2
45 °
D
А
Очевидно, что большим из этих углов является тупой угол, то есть
° + 45° =75°
Диагональ параллелограмма образует с соседними сторонам углы 30 ° и 45°.
Найдите больший угол параллелограмма.
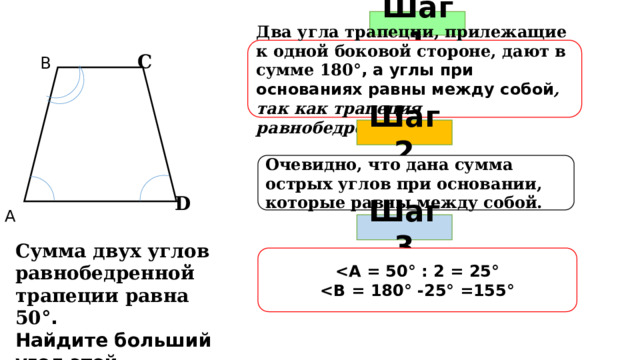
Шаг 1
Два угла трапеции, прилежащие к одной боковой стороне, дают в сумме 180 °, а углы при основаниях равны между собой , так как трапеция равнобедренная.
С
В
?
Шаг 2
Очевидно, что дана сумма острых углов при основании, которые равны между собой.
D
А
Шаг 3
Сумма двух углов равнобедренной трапеции равна 50 °.
Найдите больший угол этой трапеции.
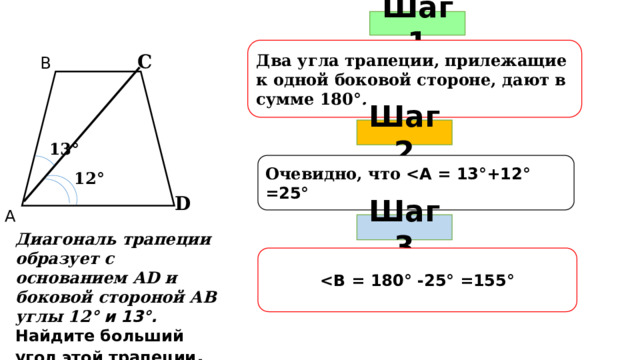
Шаг 1
Два угла трапеции, прилежащие к одной боковой стороне, дают в сумме 180 ° .
С
В
13 °
?
Шаг 2
Очевидно, что
12 °
D
А
Шаг 3
Диагональ трапеции образует с основанием АD и боковой стороной АВ углы 12 ° и 13°.
Найдите больший угол этой трапеции .
Задания для самостоятельного решения
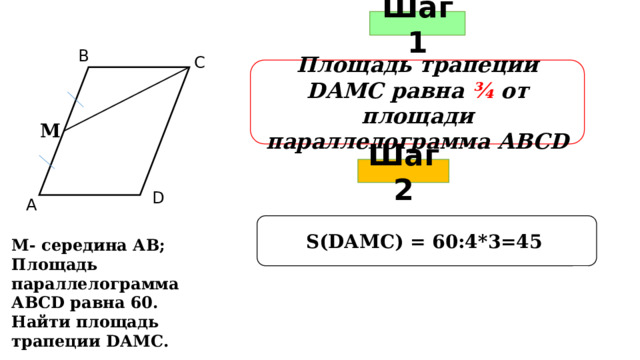
Шаг 1
В
С
Площадь трапеции DАМС равна ¾ от площади параллелограмма АВСD
М
Шаг 2
D
А
S(DАМС) = 60:4*3=45
М- середина АВ;
Площадь параллелограмма АВСD равна 60.
Найти площадь трапеции DАМС.
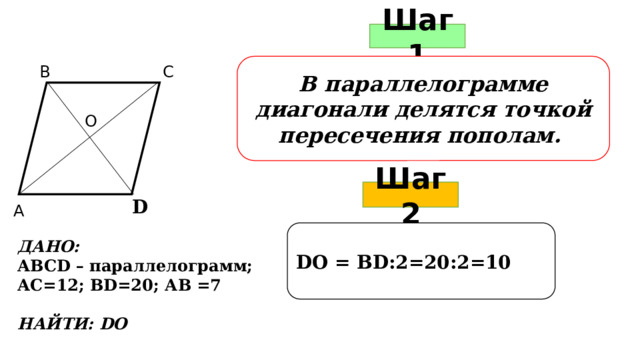
Шаг 1
В параллелограмме диагонали делятся точкой пересечения пополам.
В
С
О
Шаг 2
D
А
DО = ВD:2=20:2=10
ДАНО:
АВСD – параллелограмм;
АС=12; ВD=20; АВ =7
НАЙТИ: DО
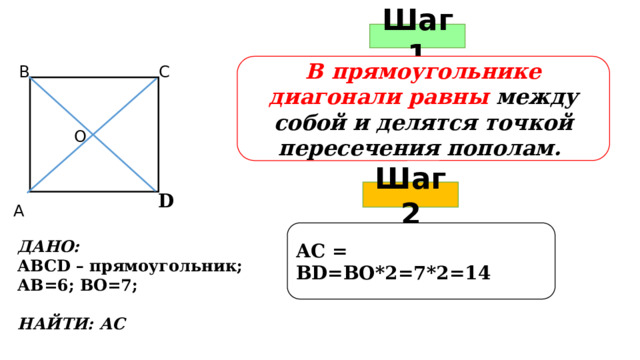
Шаг 1
В прямоугольнике диагонали равны между собой и делятся точкой пересечения пополам.
В
С
О
Шаг 2
D
А
АС = ВD=ВО*2=7*2=14
ДАНО:
АВСD – прямоугольник;
АВ=6; ВО=7;
НАЙТИ: АС
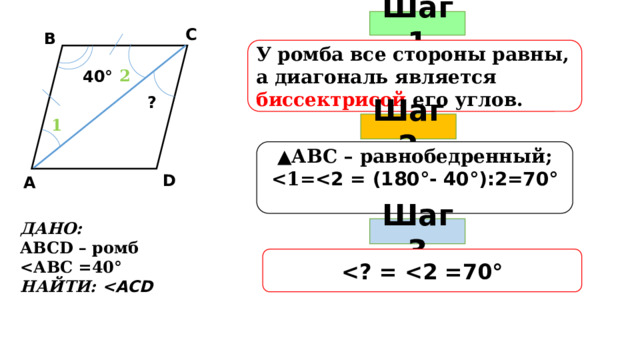
Шаг 1
С
В
У ромба все стороны равны, а диагональ является биссектрисой его углов.
2
40 °
?
1
Шаг 2
▲ АВС – равнобедренный;
D
А
ДАНО:
АВСD – ромб
°
НАЙТИ:
Шаг 3
Задания для самостоятельного решения
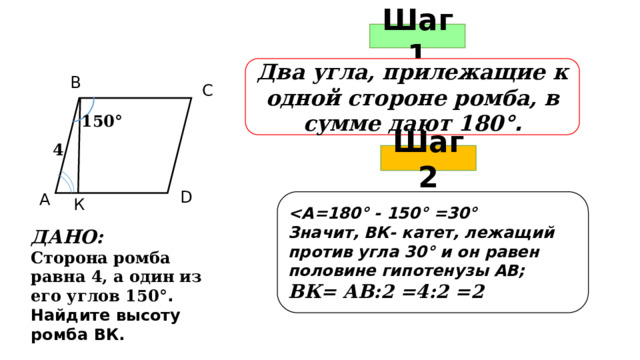
Шаг 1
Два угла, прилежащие к одной стороне ромба, в сумме дают 180 °.
В
С
150 °
4
Шаг 2
D
А
° - 150° =30°
Значит, ВК- катет, лежащий против угла 30° и он равен половине гипотенузы АВ;
ВК= АВ:2 =4:2 =2
К
ДАНО:
Сторона ромба равна 4, а один из его углов 150 °.
Найдите высоту ромба ВК.
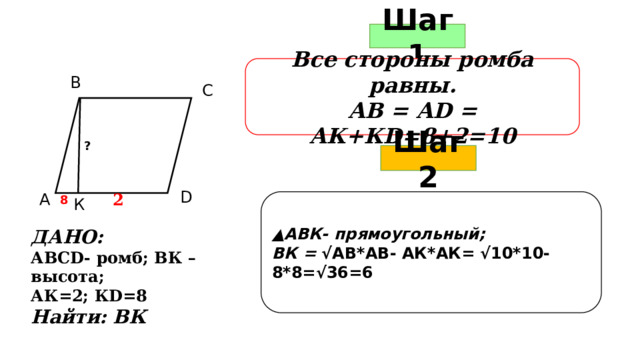
Шаг 1
Все стороны ромба равны.
АВ = АD = АК+КD=8+2=10
В
С
?
Шаг 2
D
А
2
8
▲ АВК- прямоугольный;
ВК = √АВ*АВ- АК*АК= √10*10-8*8=√36=6
К
ДАНО:
АВСD- ромб; ВК –высота;
АК=2; КD=8
Найти: ВК
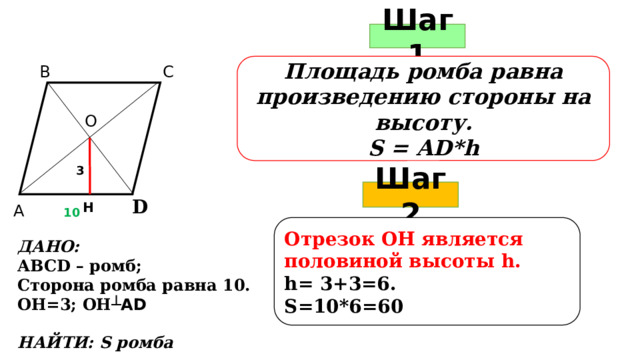
Шаг 1
Площадь ромба равна произведению стороны на высоту.
S = АD*h
В
С
О
3
Шаг 2
D
Н
А
10
Отрезок ОН является половиной высоты h.
h= 3+3=6.
S=10*6=60
ДАНО:
АВСD – ромб;
Сторона ромба равна 10.
ОН=3; ОН ┴АD
НАЙТИ: S ромба
Задания для самостоятельного решения
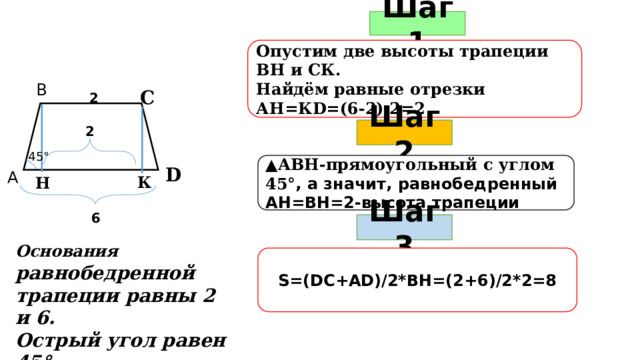
Шаг 1
Опустим две высоты трапеции ВН и СК.
Найдём равные отрезки АН=КD=(6-2):2=2
В
С
2
2
Шаг 2
2
45 °
▲ АВН-прямоугольный с углом 45 °, а значит, равнобедренный АН=ВН=2-высота трапеции
D
А
К
Н
6
Шаг 3
Основания равнобедренной трапеции равны 2 и 6.
Острый угол равен 45 °.
Найдите площадь трапеции.
S=(DC+АD)/2*ВН=(2+6)/2*2=8
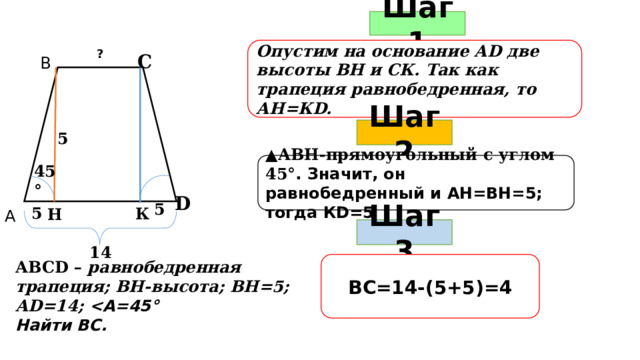
Шаг 1
Опустим на основание АD две высоты ВН и СК. Так как трапеция равнобедренная, то АН=КD.
?
С
В
?
Шаг 2
5
▲ АВН-прямоугольный с углом 45 °. Значит, он равнобедренный и АН=ВН=5; тогда КD=5
45 °
D
5
5
К
Н
А
Шаг 3
14
АВСD – равнобедренная трапеция; ВН-высота; ВН=5;
ВС=14-(5+5)=4
АD=14;
Найти ВС.
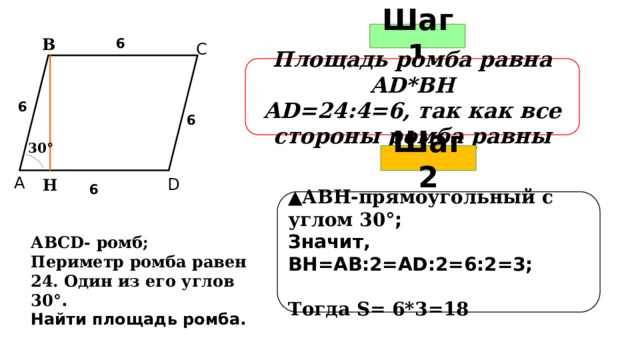
Шаг 1
В
6
С
Площадь ромба равна АD*ВН
АD=24:4=6, так как все стороны ромба равны
В
6
6
30 °
Шаг 2
А
D
Н
6
▲ АВН-прямоугольный с углом 30 °;
Значит, ВН=АВ:2=АD:2=6:2=3;
Тогда S= 6*3=18
АВСD- ромб;
Периметр ромба равен 24. Один из его углов 30 °.
Найти площадь ромба.
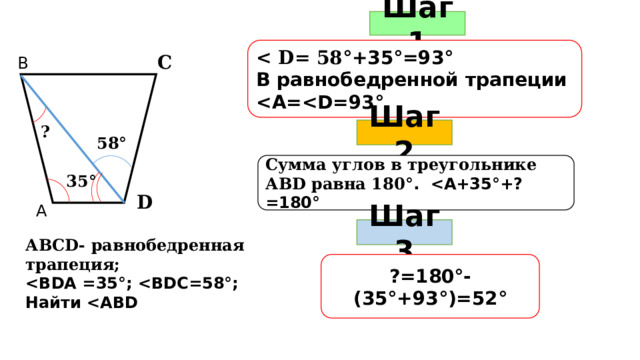
Шаг 1
°+35°=93°
В равнобедренной трапеции
С
В
?
Шаг 2
58 °
Сумма углов в треугольнике АВD равна 180 °.
35 °
D
А
Шаг 3
АВСD- равнобедренная трапеция;
Найти
?=180°-(35°+93°)=52°
Задания для самостоятельного решения
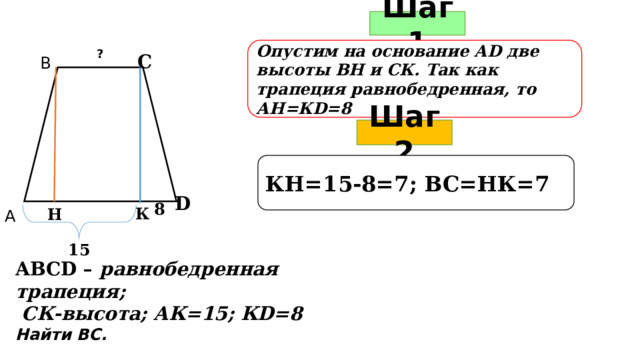
Шаг 1
Опустим на основание АD две высоты ВН и СК. Так как трапеция равнобедренная, то АН=КD=8
?
С
В
?
Шаг 2
КН=15-8=7; ВС=НК=7
D
8
К
Н
А
15
АВСD – равнобедренная трапеция;
СК-высота; АК=15; КD=8
Найти ВС.
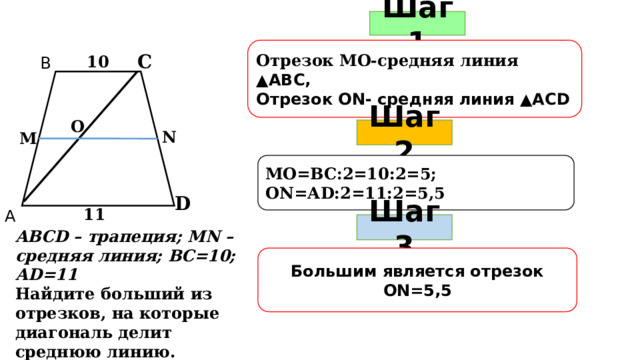
Шаг 1
Отрезок МО-средняя линия ▲АВС,
Отрезок ОN- средняя линия ▲АСD
С
10
В
О
?
Шаг 2
N
М
МО=ВС:2=10:2=5;
ОN=АD:2=11:2=5,5
D
11
А
Шаг 3
ABCD – трапеция; MN –средняя линия; ВС=10; АD=11
Найдите больший из отрезков, на которые диагональ делит среднюю линию.
Большим является отрезок ОN=5,5
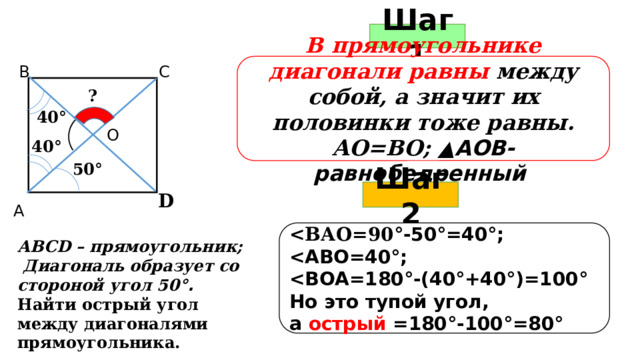
Шаг 1
В прямоугольнике диагонали равны между собой, а значит их половинки тоже равны.
АО=ВО; ▲АОВ-равнобедренный
В
С
?
40 °
О
40 °
50 °
Шаг 2
D
А
°-50°=40°;
Но это тупой угол,
а острый =180°-100°=80°
АВСD – прямоугольник;
Диагональ образует со стороной угол 50 °.
Найти острый угол между диагоналями прямоугольника.
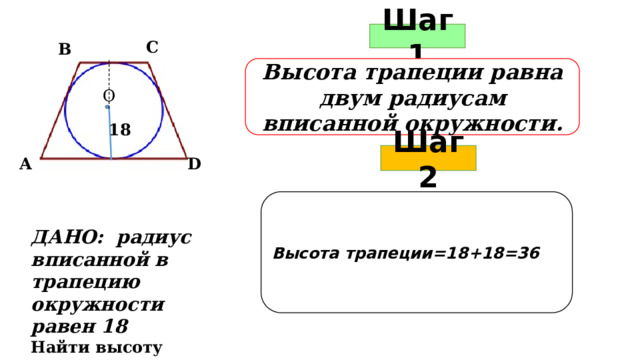
Шаг 1
С
В
Высота трапеции равна двум радиусам вписанной окружности.
О
18
Шаг 2
А
D
Высота трапеции=18+18=36
ДАНО: радиус вписанной в трапецию окружности равен 18
Найти высоту трапеции.
Задания для самостоятельного решения
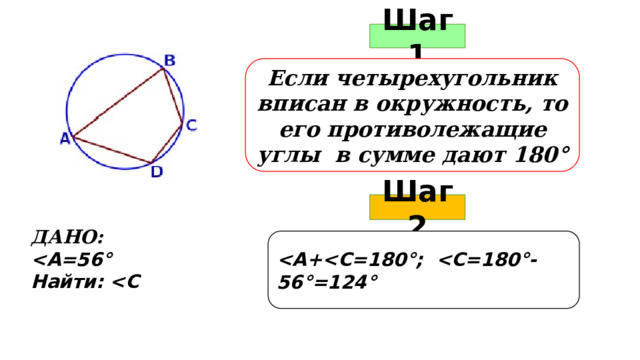
Шаг 1
Если четырехугольник вписан в окружность, то его противолежащие углы в сумме дают 180 °
Шаг 2
ДАНО:
Найти:
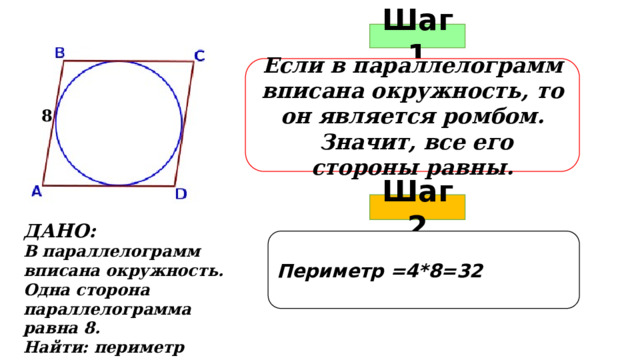
Шаг 1
Если в параллелограмм вписана окружность, то он является ромбом.
Значит, все его стороны равны.
8
Шаг 2
ДАНО:
В параллелограмм вписана окружность. Одна сторона параллелограмма равна 8.
Найти: периметр параллелограмма
Периметр =4*8=32
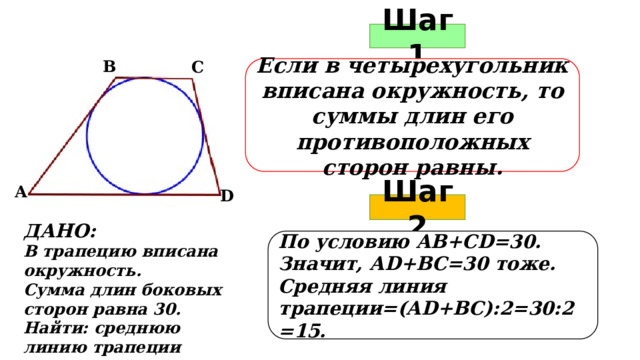
Шаг 1
В
С
Если в четырехугольник вписана окружность, то суммы длин его противоположных сторон равны.
А
D
Шаг 2
ДАНО:
В трапецию вписана окружность.
Сумма длин боковых сторон равна 30.
Найти: среднюю линию трапеции
По условию АВ+СD=30. Значит, АD+ВС=30 тоже.
Средняя линия трапеции=(АD+ВС):2=30:2=15.
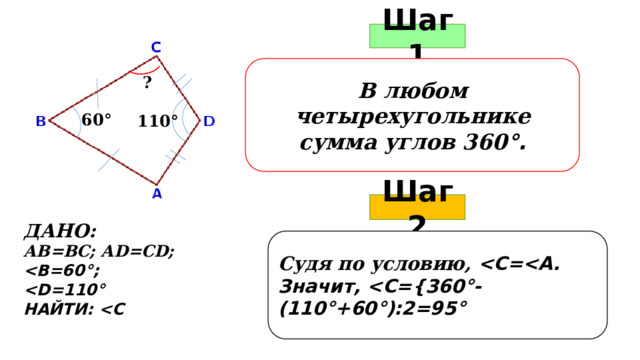
Шаг 1
В любом четырехугольнике сумма углов 360 °.
?
60 °
110 °
Шаг 2
ДАНО:
АВ=ВС; АD=CD;
НАЙТИ:
Судя по условию,
Значит,
Задания для самостоятельного решения
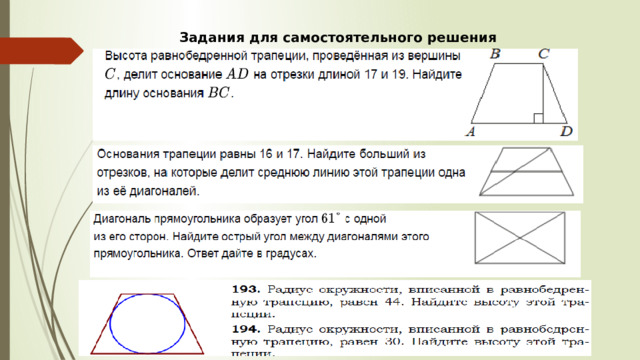
Использованные материалы
1. Задачи Открытого банка ОГЭ сайта ФИПИ; http://oge.fipi.ru/os/xmodules/qprint/index.php?proj=DE0E276E497AB3784C3FC4CC20248DC0