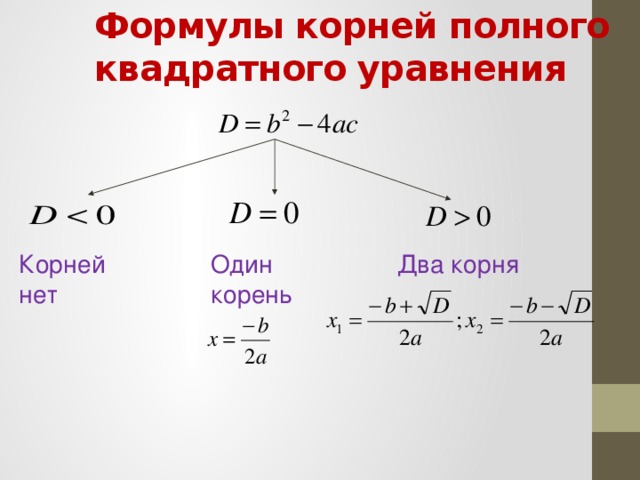
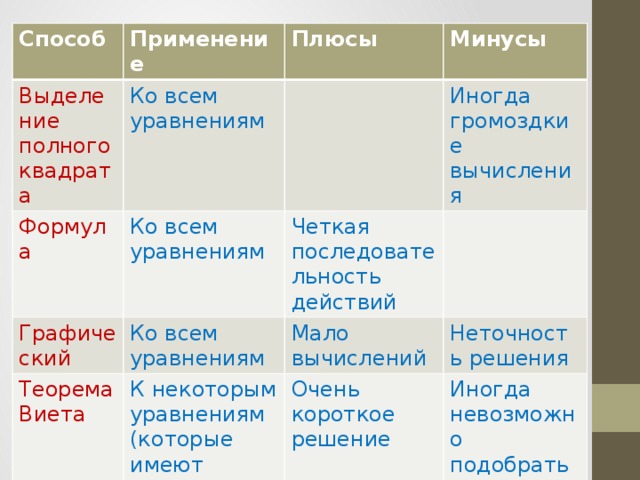
Данная презентация предназначена для использования на этапе обобщения и систематизации знаний по теме квадратные уравнения. Рассмотрены неполные и полные квадратные уравнения (4 способа решения: метод выделения полного квадрата, с помощью формулы,графический способ и с помощью теоремы Виета) Перед каждым теоретическим блоком учащимся предлагаются разноуровневые задания, что позволяет реализовать дифференцированный подход. Презентация может быть использована и в 9 классе с целью повторения и подготовки к ОГЭ
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Квадратные уравнения - способы решения.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Квадратные уравнения - способы решения. »
Полезное для учителя
Распродажа видеоуроков!
1460 руб.
2090 руб.
1670 руб.
2380 руб.
1650 руб.
2350 руб.
1670 руб.
2380 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
800 руб.
4000 руб.
2760 руб.
13800 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




 0 -два решения: х 1 = и х 2 =- Если –с/а - нет решений х(ах + в) = 0 1. х 2 = 0 2. х=0 или 2.Одно решение: х = 0. ах + в = 0 3. х = 0 и х = -в/а" width="640"
0 -два решения: х 1 = и х 2 =- Если –с/а - нет решений х(ах + в) = 0 1. х 2 = 0 2. х=0 или 2.Одно решение: х = 0. ах + в = 0 3. х = 0 и х = -в/а" width="640"