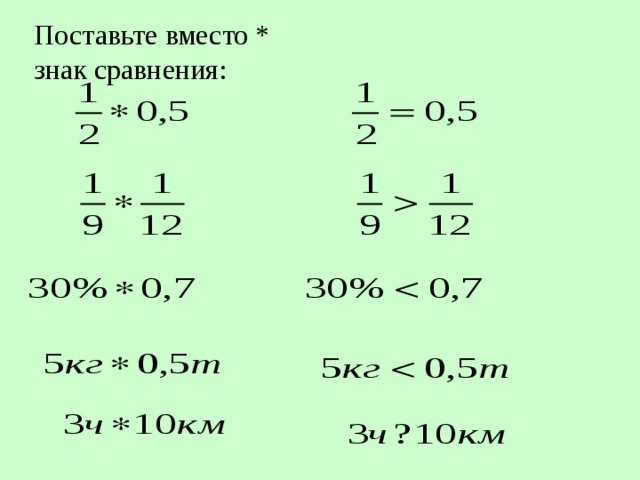ПЛАН-КОНСПЕКТ УРОКА
1. ФИО Пискунович Тамара Владимировна
2. Место работы МБОУ «Сайгинская СОШ»
3. Должность учитель математики
4. Предмет математика
5. Класс 6
6. Тема и номер урока в теме Отношение величин (первый урок из четырех по данной теме)
Тип урока: изучение нового материала.
Основные цели:
Сформировать понятие отношения, способность к упрощению отношений и нахождению отношений чисел и величин.
Повторить и закрепить: разностное и кратное сравнения чисел и величин; совместные действия с обыкновенными и десятичными дробями.
Ход урока
1) Самоопределение к деятельности (организационный момент).
Здравствуйте, ребята! Сегодня мы продолжим работать с числами.
Пусть сегодняшний день принесёт вам радость общения. Пусть вам помогут сообразительность, смекалка и те знания, которые вы уже приобрели.
2) Актуализация знаний и фиксация затруднения в деятельности.
2.1. Устная работа.
СЛАЙД2. Мы умеем сравнивать числа и величины. Какие знаки сравнения при этом используем? ()
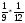
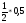 СЛАЙД3. Поставьте вместо звездочки знак сравнения :
СЛАЙД3. Поставьте вместо звездочки знак сравнения :
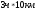
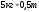
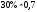
Вывод о сравнении (не все величины подлежат сравнению).
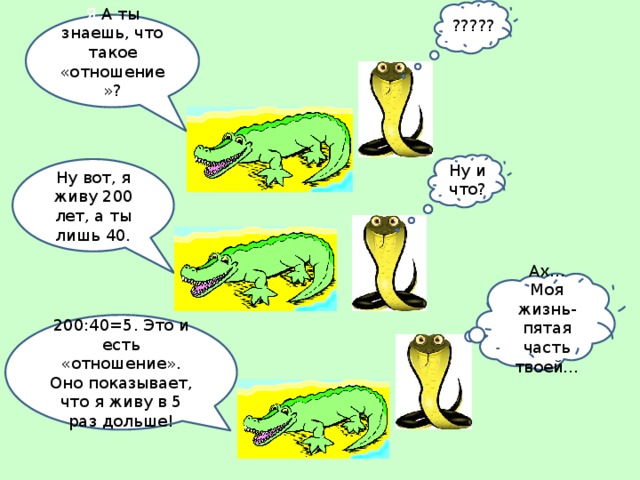
СЛАЙД 4.- Решите задачу: “Кобра живет около 40 лет, а крокодил - около 200 лет. Как можно сравнить продолжительность их жизни?
СЛАЙД 5.А) 200-40=160 (лет). На 160 лет крокодил живет больше, чем кобра.
Б) 200:40=5 (раз). В 5 раз кобра живет меньше, чем крокодил.
В) 40:200=1/5(часть).
Продолжительность жизни кобры составляет пятую часть продолжительности жизни крокодила.
(Поднимите руки, кто решил задачу. Выслушать ребят, решивших разными способами.)
- Какие “уточняющие” вопросы можно задать при решении этой задачи? (С помощью каких действий можно сравнивать? Как записать «какую часть составляет жизнь кобры от жизни крокодила»?)
- Какими способами сравнения вы пользовались? (находили разность или частное).
Существует два способа сравнения величин.
СЛАЙД 6. Первый способ состоит в нахождении их разности и отвечает на вопрос “На сколько больше (меньше) ?” Это сравнение называется разностное. Второй состоит в нахождении частного и отвечает на вопрос “ Во сколько раз больше (меньше) ?” Это сравнение - кратное.
2.2 СЛАЙД 7. Решите задачу- шутку “ Кто сильнее: слон или муравей?»
СЛАЙД 8.«Вес муравья примерно 50 миллиграммов или 0.05 г, а слона 5 тонн. При этом муравей способен поднять груз весом в 0.5 г, а слон в полторы тонны. Так кто из них сильнее?»
(Выслушать решение, направить ход рассуждений. Дать установку: узнайте, во сколько раз тяжелее груз который может поднять муравей , чем весит он сам. То же проделайте со слоном.)
Решение: Если соотнести вес поднимаемого груза и собственный вес ( 0.5/0.05=10 и 1.5/5= 0.3), получится, что муравей поднимает груз в 10 раз больше чем весит сам, а слон - три десятых от своего веса. Наверно неспроста в честь трудолюбивого мураша был назван грузовой трехколесный мотороллер «Муравей».
Итак, соотнести силы муравья и слона нам помогло какое сравнение? (КРАТНОЕ)
3) Постановка учебной задачи.
- Над каким вопросом будем сегодня работать?
(Будем рассматривать кратное сравнение величин).
- Это - цель урока.
Для результата кратного сравнения двух величин в математике часто используют термин “отношение”.
- А теперь сформулируйте тему урока. (Отношения величин).
СЛАЙД 9.- Молодцы! Запишите тему в тетрадях.
(Учитель записывает на доске: Отношения величин).
4) Построение проекта выхода из затруднения. Открытие детьми “нового знания”.
4.1.
- Как записать отношение чисел из задачи по кобру и крокодила? Каким действием определяем «во сколько раз или какую часть составляет»? (кто знает, запишите на доске)
СЛАЙД 10.(Составить частное чисел 200 и 40).
- Итак, отношение находят делением .
-Откройте стр. 118 учебника и прочитайте рубрику «Говори правильно»
- А теперь прочитайте данное отношение тремя способами.
(1-отношение числа двести к числу сорок;
2-отношение чисел двести и сорок;
3-отношение двухсот к сорока).
4.2. –Мы уже с вами знаем, что такое «Определение» и можем дать определение делителя, кратного, взаимно обратным числам.
СЛАЙД 11.Вернемся к задаче про кобру и крокодила. Прочитайте на слайде диалог животных. А теперь попытайтесь составить определение понятия «отношения».
Наводящие вопросы:
-Каким действием находим отношение? Результат деления?
-Могут ли числа быть равными нулю?
-Что показывает отношение?
А теперь, обозначим в задаче про кобру и крокодила за a-возраст крокодила, а за b-возраст кобры и составим определение для отношения чисел aиb.
Предполагаемый ответ учащихся с наводящими вопросами учителя:
«Отношением чисел а и b называется:
1.Частное двух чисел а и в;
-имеет ли смысл кратное сравнение чисел, хотя бы одно из которых равно нулю?
2. числа отличны от нуля;
–какую информацию можно получить из отношения?
(Во сколько раз больше, меньше, какую часть составляет одно число от другого).
3.Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.»
-Попробуйте соединить все выводы и сами сформулировать определение отношения. (После заслушивания формулировок предложить учащимся прочитать определение на стр.117 учебника).
СЛАЙД 12.4.3 - На клумбе 6 белых и 12 красных роз. Что показывают отношения?
а) 6:12
б) 12:6
в) 6:18
г) 18:12
а) Число белых роз составляет половину числа красных роз.
б) Число красных роз в 2 раза больше числа белых роз.
в) Какую часть составляют белые розы от числа всех цветов на клумбе.
г) Во сколько раз число всех цветов на клумбе больше числа красных роз.
- Чему равны отношения?
- Обратите внимание на случаи а), б). Как называются такие числа?
(Взаимно обратные).
- Что заметили при вычислении?
(Отношения можно “упрощать”; записав их в виде дроби, можно сокращать эту дробь).
- Отношение иногда бывает удобно выражать в процентах. Как представить число в %?
(Умножить на 100%). Выразите в процентах, что удобно.
5) Первичное закрепление во внешней речи.
–Выполним в тетрадях упражнение № 722 (б,в,г). (у доски по одному ученику: записывает, читает, переводит в проценты)
Б)6:20=0,3=30%
В)12,3:3=4,1=410%
Г)9,1:0,07=130=13000%
СЛАЙД 13. - Выполни задание : (в тетради по вариантам и на закрытой доске-2 ученика по вариантам по карточкам) (см. приложение)
1вариант В классе 10 мальчиков и 15 девочек.
2вариант В тетради 12 листов, из них 4 исписано.
- По данному условию составьте какие-нибудь отношения (не менее двух) и объясните их смысл. Упростите, если возможно, полученные отношения; если удобно, выразите в процентах.
СЛАЙД 14.Решения:
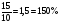 1вариант
1вариант
.
Девочек в классе в 1,5 раза больше, чем мальчиков; девочек на 50% больше.
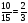
-
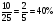 Мальчики составляют две трети от числа девочек.
Мальчики составляют две трети от числа девочек.
3)
Составляют мальчики от класса.
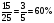
4)
Составляют девочки от класса.
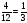
2вариант
1)
Третья часть тетради исписана.
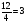
2)
В тетради всего в 3 раза больше листов, чем исписанных.
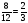
3)
Две трети тетради не исписана.
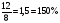
4)
В тетради всего в полтора раза больше листов, чем не исписанных.
6) Физпауза
Мы все вместе улыбнемся,
Подмигнем слегка друг другу,
Вправо, влево повернемся (поворот влево - вправо)
И кивнем затем по кругу(наклоны влево – вправо)
Все идеи победили,
Вверх взметнули наши руки(поднимают руки вверх – вниз)
Груз забот с себя стряхнули,
И продолжим путь науки (встряхнули кисти рук).
7) Самостоятельная работа с самопроверкой по эталону на доске.( у кого все верно поставьте 5, кто не выразил в процентах -4, остальным – найти ошибки и исправить)
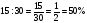
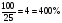 - Найдите отношения, если удобно – выразите в процентах:
- Найдите отношения, если удобно – выразите в процентах:
а) б)
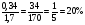
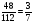
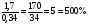 в) г)
в) г)
д)
8) Рефлексия деятельности. (Итог урока).
- Что сегодня мы нового узнали на уроке?
- Над чем еще надо поработать?
- Кого вы можете отметить?
- Оцените свою работу на уроке. (поставьте восклицательный знак, если все понятно; если есть вопросы, вопросительный знак)
9) Домашнее задание: п.20, отв. На вопросы, № 722(а,д,е), 723, 747
Оборудование:
1.ноутбук;
2.мультимедийный проектор;
3.экран;
4.раздаточный материал (карточки с заданиями)
УМК:
1.Виленкин Н.Я. Математика. 6 класс : учеб.для общеобразоват. Учреждений / Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. – 30-е изд., стер. – М. : Мнемозина, 2013.-288 с. : ил.;
2.Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 6 класса. М. : Просвещение, 2012.
Приложение №1
2 вариант
В тетради 12 листов, из них 4 исписано.
- По данному условию составьте какие-нибудь отношения (не менее двух) и объясните их смысл. Упростите, если возможно, полученные отношения; если удобно, выразите в процентах.
1 вариант
В классе 10 мальчиков и 15 девочек.
- По данному условию составьте какие-нибудь отношения (не менее двух) и объясните их смысл. Упростите, если возможно, полученные отношения; если удобно, выразите в процентах.
Технологическая карта урока
| № | Этап урока | Название используемых ЭОР | Деятельность учителя | Деятельность ученика | Время(мин) | Формируемые УУД |
| Познаватель ные | Регулятив ные | Коммуника тивные | Личност ные |
| 1 | Орг. момент |
| приветствие уч-ся, проверка учителем готовности класса к уроку, орг-ция внимания; | настраиваются на работу; | 2 | осознанное и произвольное построение речевого высказывания; | прогназирование своей деят-ти | умение слушать и вступать в диалог | умение выделять нравственный аспект поведения |
| 2 | Вводная беседа. Актуализация знаний | слайды №2,3,4,5,6,7. | вступительное слово учителя; повторение умений сравнивать числа и величины. действия с десятичными и обыкновенными дробями; учитель начинает беседу с проблемной задачи по будущей теме урока; задает ученикам наводящие вопросы; | участвует в работе по повторению; в беседе с учителем отвечает на поставленные вопросы; | 10 | поиск и выделение необходимой информации | выделение и осознание того,что уже пройдено; постановка цели учебной задачи, синтез; | умение с достаточной полнотой и точностью выражать свои мысли; слушать и вступать в диалог; уметь устно и письменно выражать свои мысли; | адекватное понимание причин успеха( не успеха) в учебной деятельности; |
| 3 | Изучение нового материала | слайды №8,9. | помогает ученикам определять цель урока | учащиеся определяют тему урока; | 8 | построение логической цепи рассуждений; формирование обобщать , составлять алгоритм математическ. действий; | целеполагание, выдвижение гипотез; | умение слушать и вступать в диалог; | Овладение на уровне общего образования законченной системы математич. знаний; |
| 4 | Первичное осмысление и закрепление знаний | слайды №10,11. | комментирует, направляет работу уч-ся; | один ученик на доске, а остальные в тетради выполняют | 10 | выделение и формулирование познават. цели; рефлексия способов и условий действия | планирование своей деятельности для решения поставленной задачи и контороль полученного результата; | умение слушать и вступать в диалог; коллективное обсуждение проблем (при необходимости); | оценка выделять и осознавать уч-ся того, что уже усвоено |
| 5 | Физпауза |
| сменить деятельность; обеспечить эмоциональную разгрузку уч-ся; | уч-ся сменили деятельности (отдохнули и готовы продолжать работу); | 2 |
|
|
|
|
| 6 | Закрепление изученного. Решение задач | самостоят. работа по карточкам (приложение №1) | выступает в роли помощника для слабых уч-ся; | уч-ся выполняют задания по карточкам; делают записи в тетрадях; после выполнения задания выполняют взаимную проверку; | 10 | выбор наиболее эффектных способов решения задач в зависимости от конкретного условия;
| планирование своей деятельности для решения поставленной задачи, контроль полученного результата; | умение слушать и вступать в диалог; | осознание ценностей математическ. знаний;
|
| 7 | Подведение итогов урока. Оценивание знаний. Рефлексия деят-ти. |
| учитель подводит итог урока, оценивает знания; задает домашнее задание; | ученики оценивают свою работу на уроке; | 3 | выделение существенной информации из слов учителя; | регуляция учебной деятельности; | умение слушать учителя; | оценивание усваиваемого материала; |
9
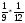
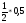 СЛАЙД3. Поставьте вместо звездочки знак сравнения :
СЛАЙД3. Поставьте вместо звездочки знак сравнения :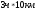
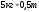
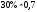
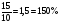 1вариант
1вариант 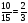
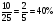 Мальчики составляют две трети от числа девочек.
Мальчики составляют две трети от числа девочек.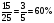
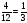
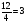
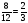
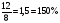
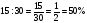
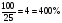 - Найдите отношения, если удобно – выразите в процентах:
- Найдите отношения, если удобно – выразите в процентах: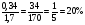
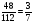
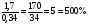 в) г)
в) г) боль ш е меньше = равно" width="640"
боль ш е меньше = равно" width="640"