Данная работа составлена для подготовки к ОГЭ. Может быть использована в конце учебного года, как повторение данной темы.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
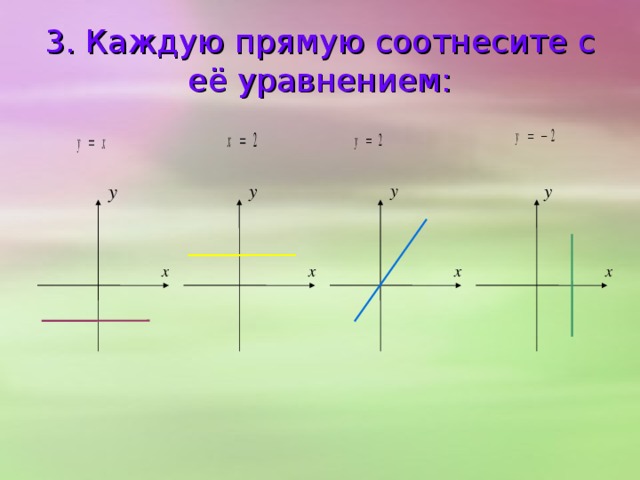
Подготовка к ОГЭ. Функции.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Подготовка к ОГЭ. Функции.»
Полезное для учителя
Распродажа видеоуроков!
1190 руб.
1980 руб.
1160 руб.
1940 руб.
1440 руб.
2400 руб.
1430 руб.
2380 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
600 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



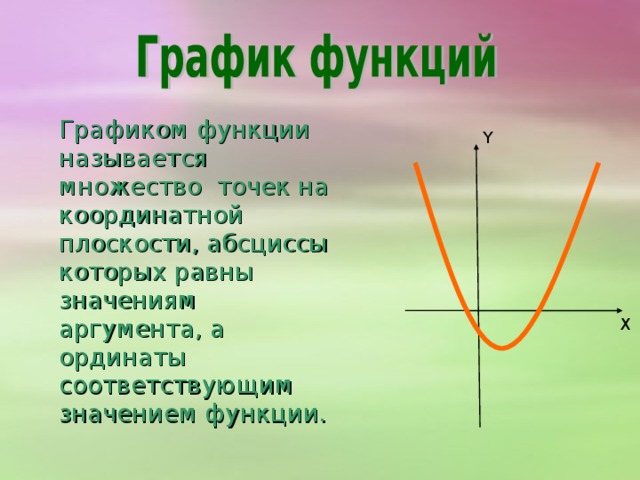




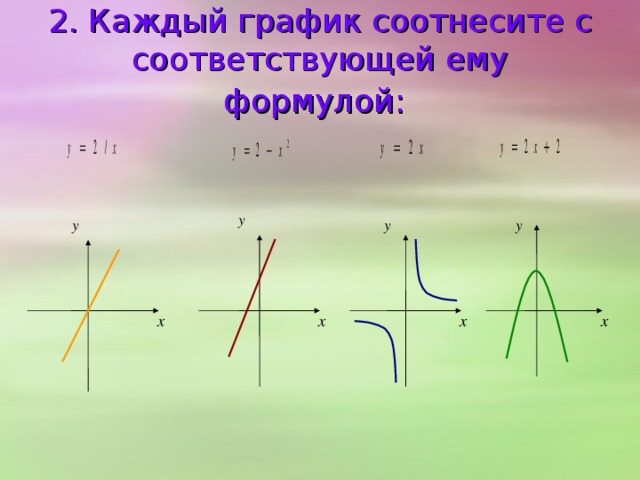
 0 - функция вида y=k / x ; область определения функции – от минус бесконечности до нуля и от нуля до бесконечности: D (f)= (-∞;0) υ (0;∞) область значений функции – вся числовая прямая, исключая нули: E (f) =(-∞;0) υ (0;∞); графиком функции является гипербола, не проходящая через начало координат. k" width="640"
0 - функция вида y=k / x ; область определения функции – от минус бесконечности до нуля и от нуля до бесконечности: D (f)= (-∞;0) υ (0;∞) область значений функции – вся числовая прямая, исключая нули: E (f) =(-∞;0) υ (0;∞); графиком функции является гипербола, не проходящая через начало координат. k" width="640"

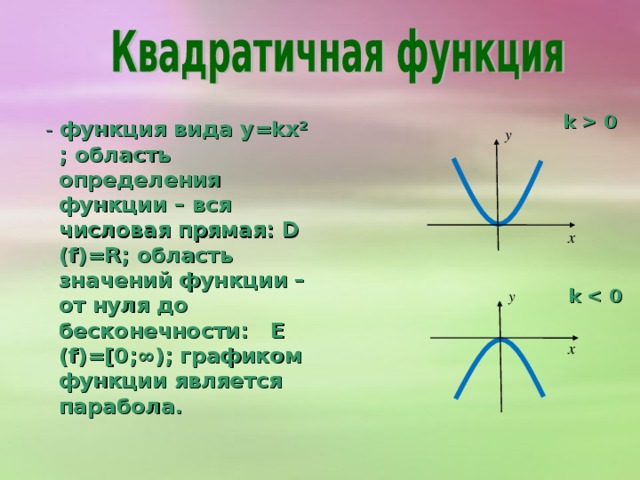
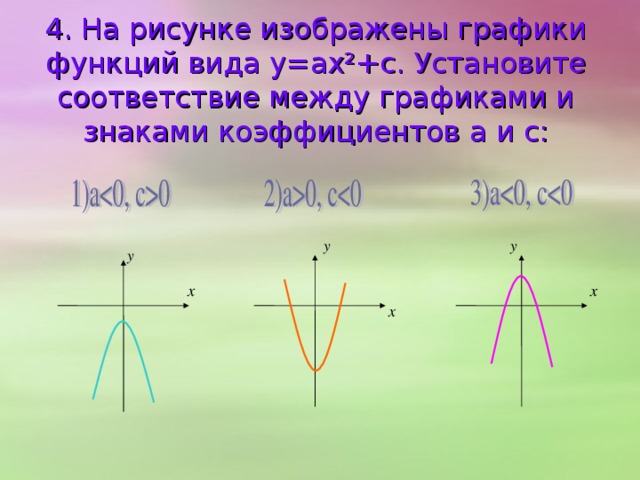
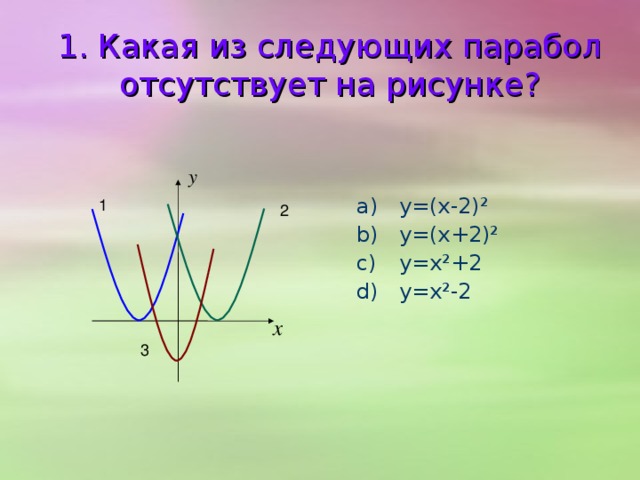 0 - функция вида y=kx² ; область определения функции – вся числовая прямая: D (f)=R; область значений функции – от нуля до бесконечности: E (f)=[ 0;∞); графиком функции является парабола . k" width="640"
0 - функция вида y=kx² ; область определения функции – вся числовая прямая: D (f)=R; область значений функции – от нуля до бесконечности: E (f)=[ 0;∞); графиком функции является парабола . k" width="640"