Презентация по теме: "Показательная функция, её свойства и график" для 10 класса, предназначена для введения нового материала. Презентация содержит теоретический материал, устный счет, задачи на первичное закрепление материала, проверочную работу. Данная презентация может быть использована для повторения метериала при подготовке к ЕГЭ.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Показательная функция, ее свойства т график
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Показательная функция, ее свойства т график»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1580 руб.
2640 руб.
1440 руб.
2400 руб.
1430 руб.
2380 руб.
1160 руб.
1940 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
3560 руб.
17800 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





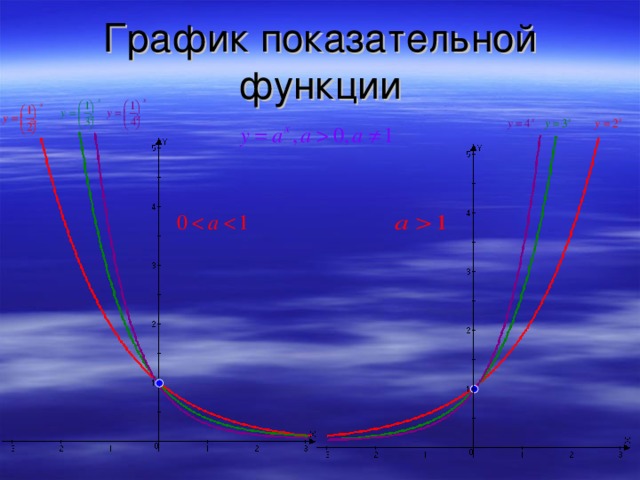
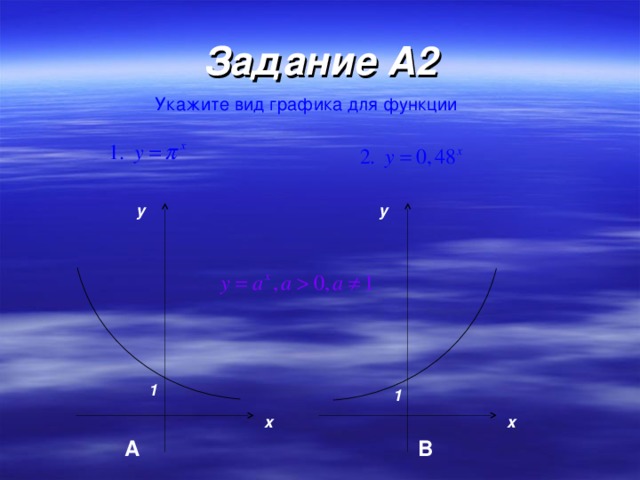


 0 при х R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а 1 и убывает на R при 0 . 7) Наибольшего и наименьшего значений у функции нет. 8) Функция непериодична. 9) Ограничена снизу, не ограничена сверху. y 1 x о" width="640"
0 при х R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а 1 и убывает на R при 0 . 7) Наибольшего и наименьшего значений у функции нет. 8) Функция непериодична. 9) Ограничена снизу, не ограничена сверху. y 1 x о" width="640"


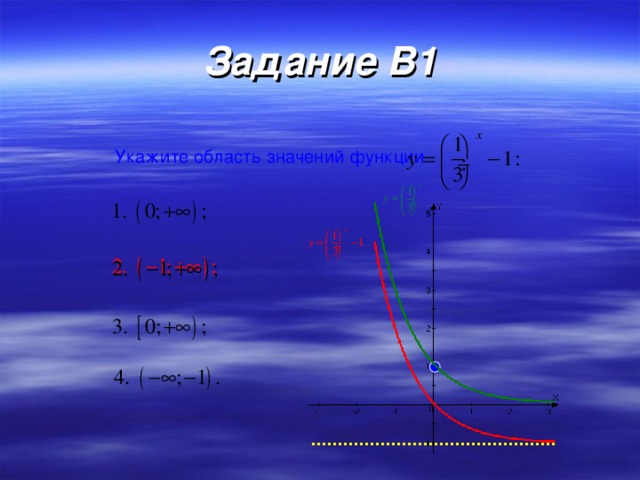




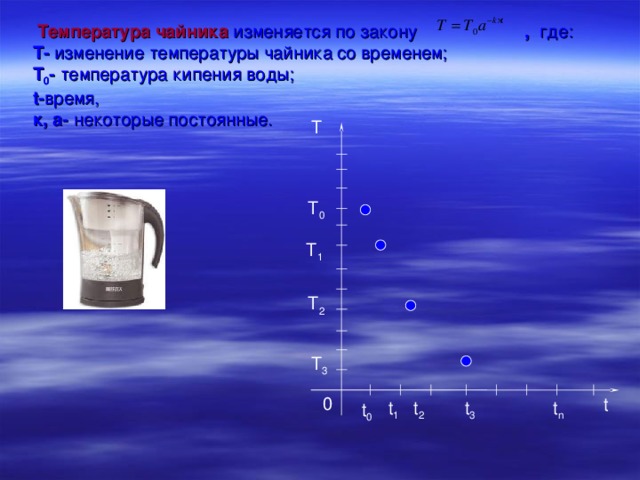


 1, след-но показательная функция возрастает. 3. Сравнить показатели степеней (или аргументы функций) 34 4. Используя свойство возрастания (убывания) функции, сравнить степени с одинаковым основанием (или значения функций) 1,3 34 1,3 40 . 5 . Сравнить исходные числа. Сравните:" width="640"
1, след-но показательная функция возрастает. 3. Сравнить показатели степеней (или аргументы функций) 34 4. Используя свойство возрастания (убывания) функции, сравнить степени с одинаковым основанием (или значения функций) 1,3 34 1,3 40 . 5 . Сравнить исходные числа. Сравните:" width="640"
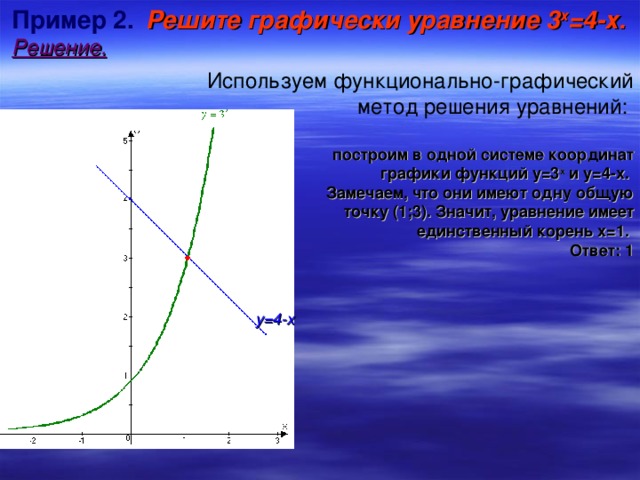

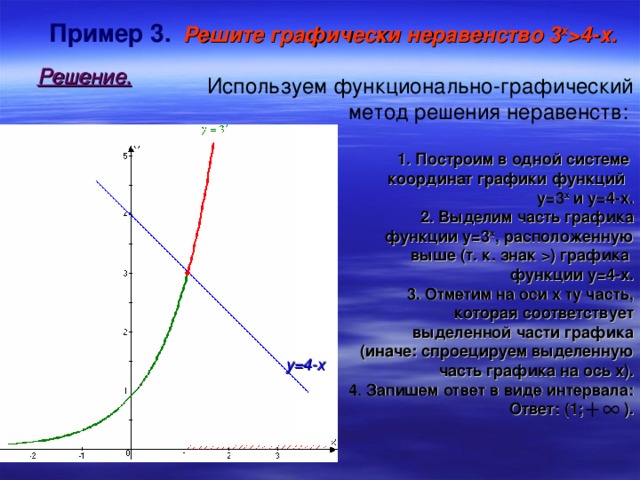 4-х. Решение. Используем функционально-графический метод решения неравенств: 1. Построим в одной системе координат графики функций у=3 х и у=4-х. 2. Выделим часть графика функции у=3 х , расположенную выше (т. к. знак ) графика функции у=4-х. 3. Отметим на оси х ту часть, которая соответствует выделенной части графика (иначе: спроецируем выделенную часть графика на ось х). 4. Запишем ответ в виде интервала: Ответ: (1; ). у=4-х" width="640"
4-х. Решение. Используем функционально-графический метод решения неравенств: 1. Построим в одной системе координат графики функций у=3 х и у=4-х. 2. Выделим часть графика функции у=3 х , расположенную выше (т. к. знак ) графика функции у=4-х. 3. Отметим на оси х ту часть, которая соответствует выделенной части графика (иначе: спроецируем выделенную часть графика на ось х). 4. Запишем ответ в виде интервала: Ответ: (1; ). у=4-х" width="640"
 1; 2) 2 х 3) (1/3 ) х 4) (1/2) x x+3 ; 5 ) 5 x 6-x ; 6) (1/3) x x+1 ." width="640"
1; 2) 2 х 3) (1/3 ) х 4) (1/2) x x+3 ; 5 ) 5 x 6-x ; 6) (1/3) x x+1 ." width="640"