Презентация предназначена для сопровождения практического занятия. В презентацию включен теоритический материал и задачи на применение производной к исследованию функций. Рассмотрены алгоритмы исследования функций на монотонность, экстремумы, правило нахождения наибольшего и наименьшего значений функции, схема исследования функции и построения ее графика. Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ. Данную презентацию можно использовать для интерактивной доски.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Презентация к практическому занятию "Решение задач по теме «Исследование функции с помощью производной»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к практическому занятию "Решение задач по теме «Исследование функции с помощью производной» »
Полезное для учителя
Распродажа видеоуроков!
1360 руб.
1940 руб.
1670 руб.
2380 руб.
1680 руб.
2400 руб.
1750 руб.
2500 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
2760 руб.
13800 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



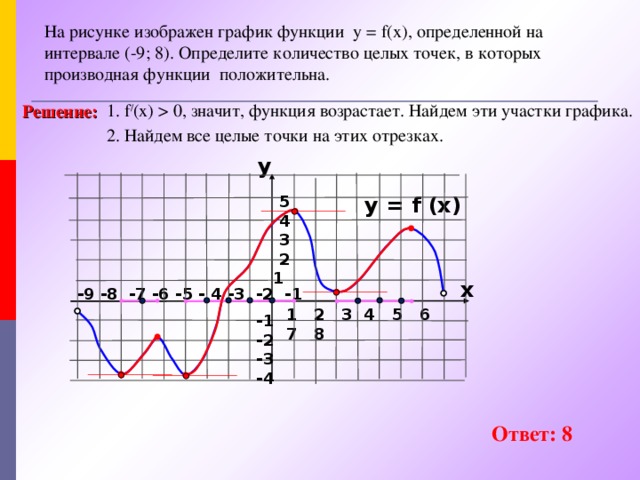 0 , значит, функция возрастает. Найдем эти участки графика. Решение: 2. Найдем все целые точки на этих отрезках. y y = f (x) 5 4 3 2 1 x -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 Ответ: 8" width="640"
0 , значит, функция возрастает. Найдем эти участки графика. Решение: 2. Найдем все целые точки на этих отрезках. y y = f (x) 5 4 3 2 1 x -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 Ответ: 8" width="640"
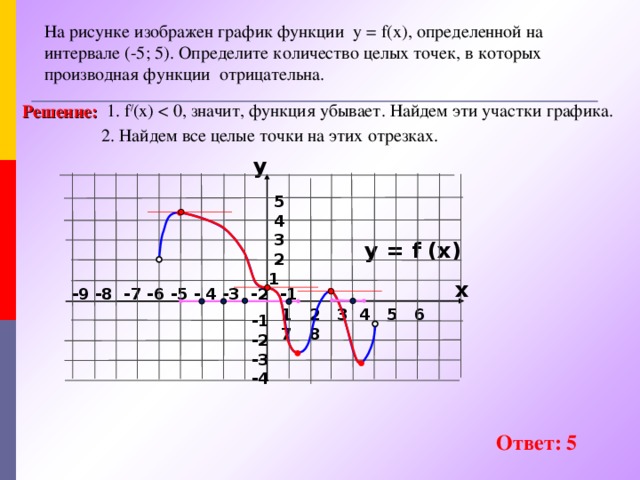
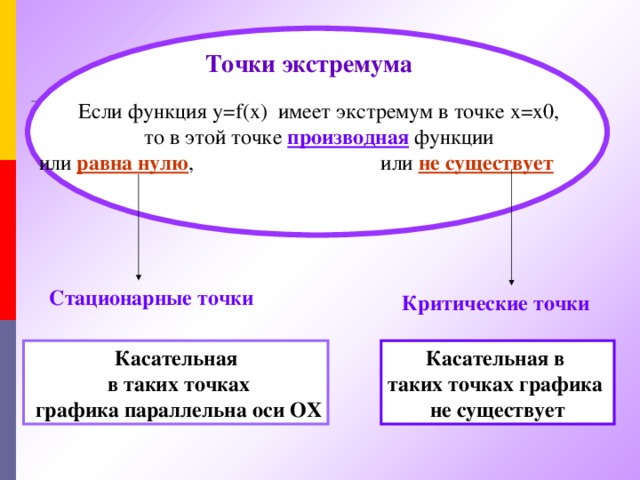
 f(x 0 ) Определение 2. Точку х=х 0 называют точкой максимума функции f (х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) Точки максимума и минимума объединяют общим термином – точки экстремума" width="640"
f(x 0 ) Определение 2. Точку х=х 0 называют точкой максимума функции f (х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) Точки максимума и минимума объединяют общим термином – точки экстремума" width="640"
![Непрерывная функция у = f(x) задана на отрезке [ a;b ] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y y = f(x) b a x http://mathege.ru:8080/or/ege/Main?view=TrainArchive Ответ: 5 9 9](https://fsd.kopilkaurokov.ru/uploads/user_file_543ec7e449598/img_user_file_543ec7e449598_8.jpg)

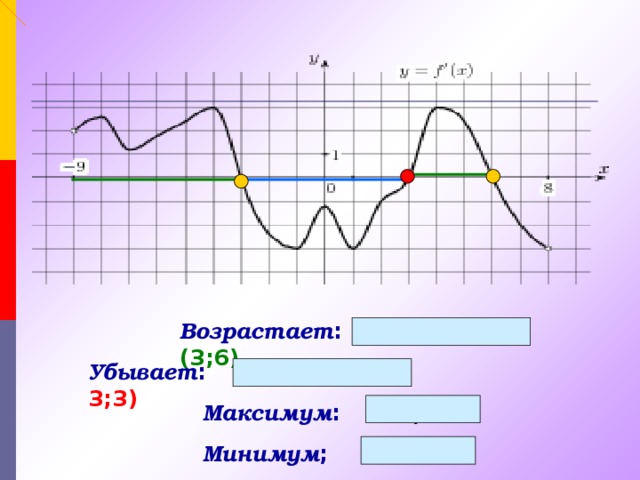
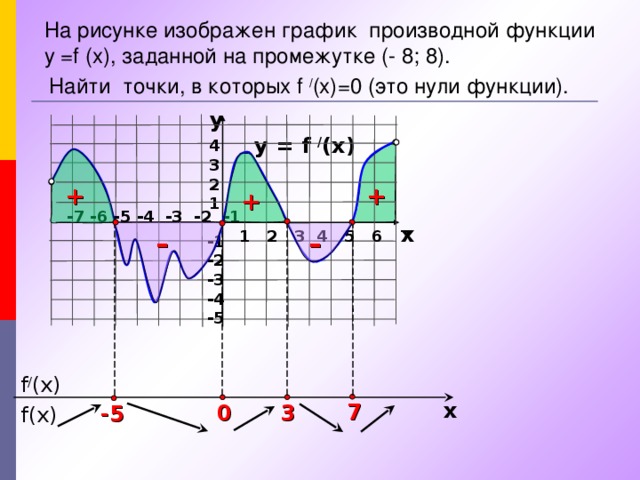
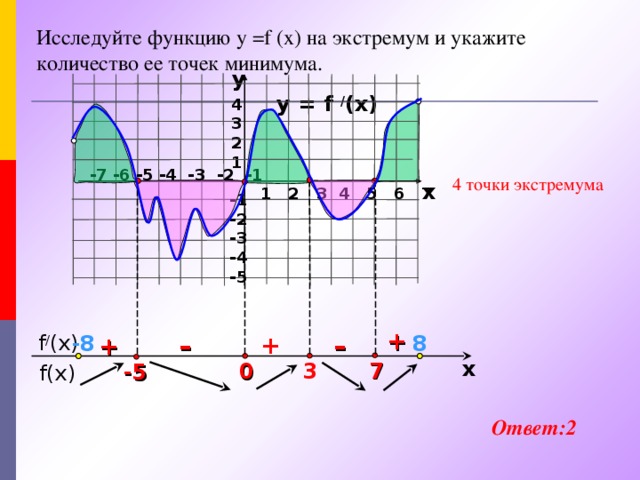
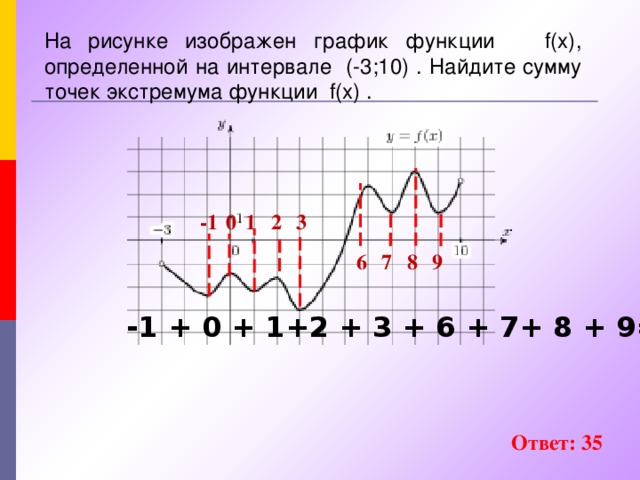
![Найдите количество точек экстремума функции у = f (x) на отрезке [ – 3; 7 ] y y = f / (x) 4 3 2 1 -7 -6 -5 -4 -3 -2 -1 x 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 + 8 f / (x) - 8 + – + – x 3 0 7 -5 f(x) Ответ: 3](https://fsd.kopilkaurokov.ru/uploads/user_file_543ec7e449598/img_user_file_543ec7e449598_13.jpg)


![Найти промежутки монотонности функции y=x³-3x² Область определения : R . Функция непрерывна. Вычисляем производную : y’= 3 x²-6x. Находим критические точки: y’= 0. x²- 2 x = 0 x(x-2)= 0 x 1 =0 и x 2 =2 Делим область определения на интервалы: + - + 2 0 5. Функция возрастает при x ϵ (-∞;0] υ [2;+∞) , функция убывает при x ϵ [0 ; 2] . 14](https://fsd.kopilkaurokov.ru/uploads/user_file_543ec7e449598/img_user_file_543ec7e449598_17.jpg)






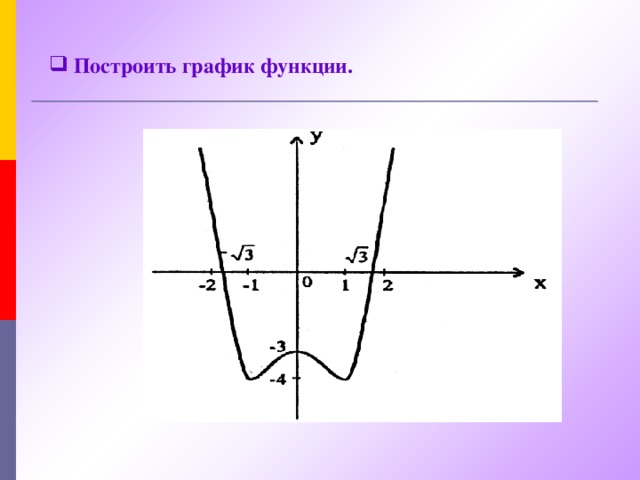
![Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b] Чтобы найти наибольшее и наименьшее значения непрерывной функции f(x) на промежутке [a;b] , нужно вычислить её значения f(a) и f(b) на концах данного промежутка; вычислить её значения в критических точках, принадлежащих этому промежутку; Выбрать из них наибольшее и наименьшее . Записывают : max f(x) и min f(x) [a;b] [a;b]](https://fsd.kopilkaurokov.ru/uploads/user_file_543ec7e449598/img_user_file_543ec7e449598_25.jpg)






















