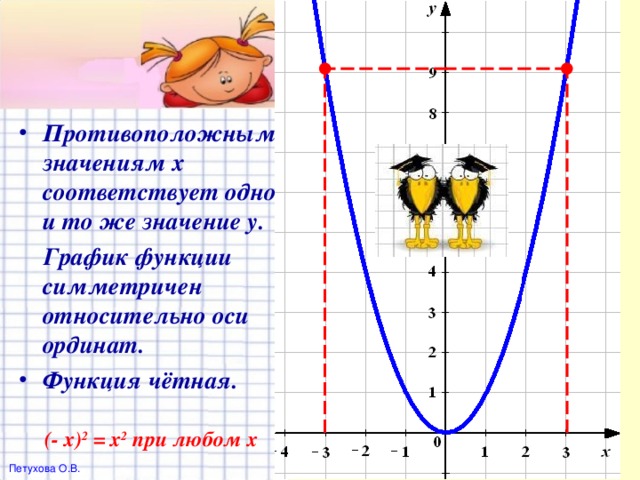
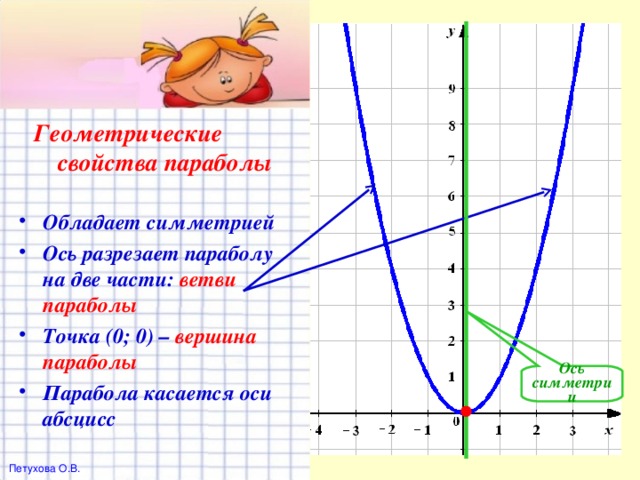
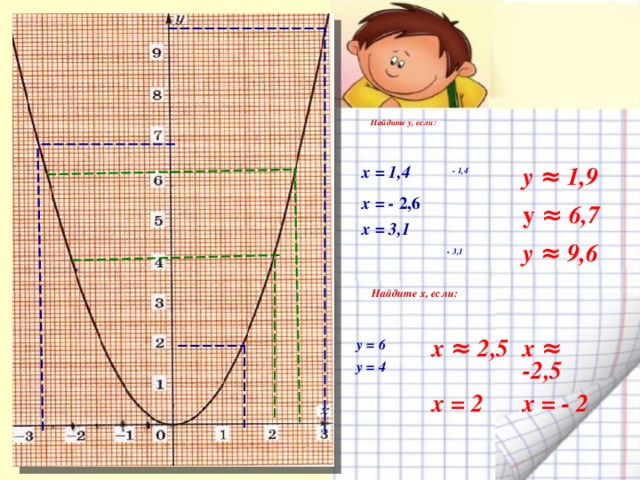
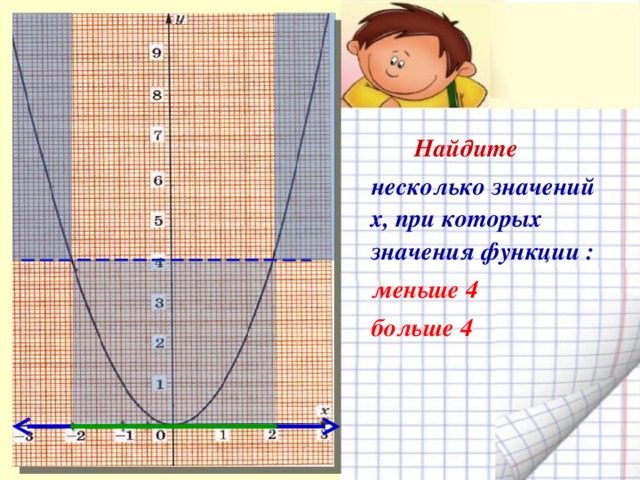
В презентации показывается как строить график функции, рассматриваются её свойства. Часть презентации посвящена историческим сведениям, использованию свойств параболы и т. д. В активном режиме выполняются задания на выработку основных умений и навыков. Предоставляя высокую степень наглядности, данный материал поможет учителю повысить эффективность обучения, даст возможность более рационально распределить время на уроке. При помощи анимационных эффектов, выделения понятий и важных моментов цветом, внимание учеников акцентируется на изучаемом предмете, достигается лучшее запоминание определений и хода рассуждения при решении задач.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Презентация к уроку №9 (Функции y=ax2, y=ax3)
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«презентация к уроку №9 (Функции y=ax2, y=ax3) »
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
1750 руб.
2500 руб.
1680 руб.
2400 руб.
1680 руб.
2400 руб.
Курсы ПК и ППК для учителей!
3560 руб.
17800 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
500 руб.
2500 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





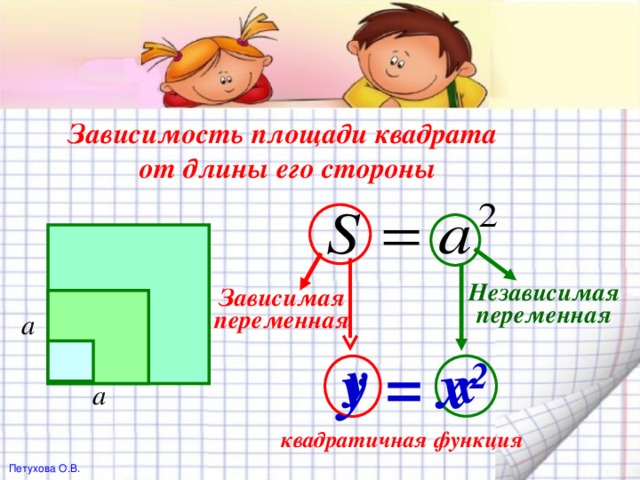


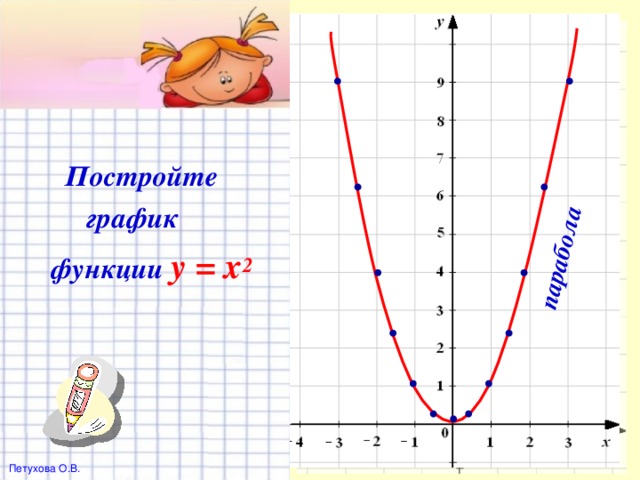

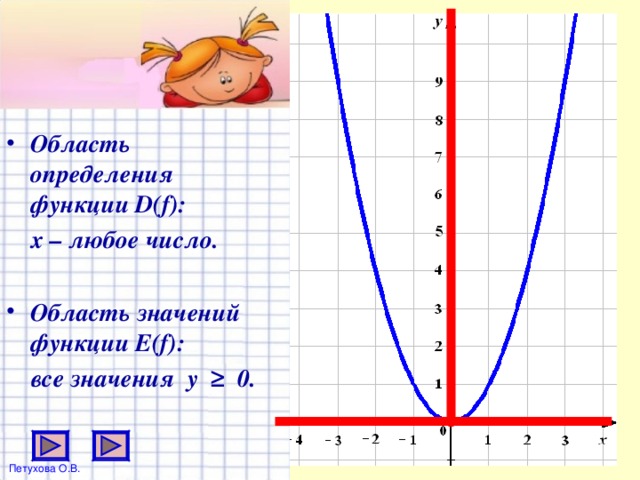
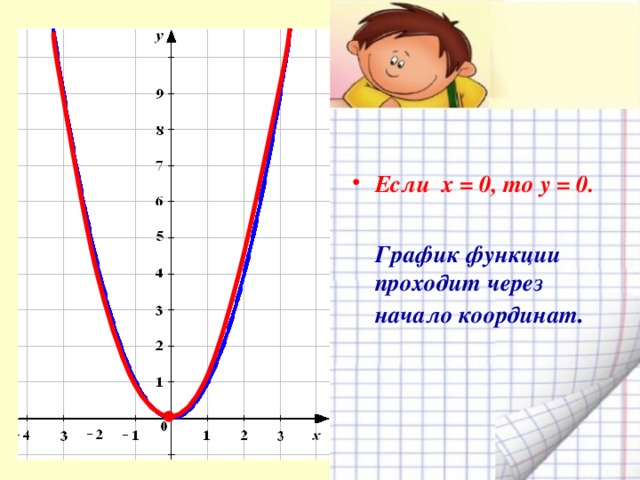
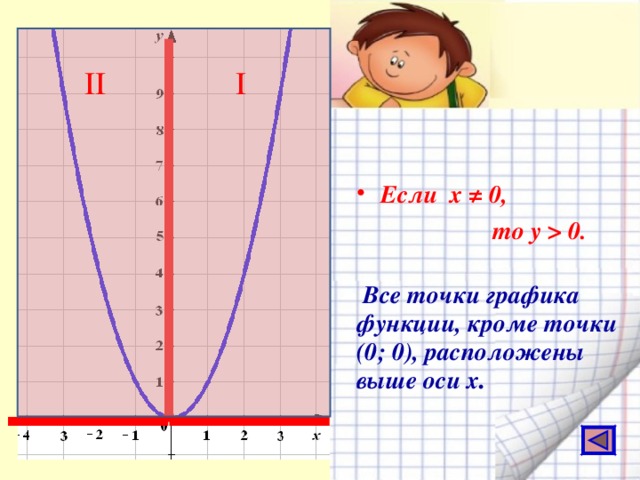 0. Все точки графика функции, кроме точки (0; 0), расположены выше оси х ." width="640"
0. Все точки графика функции, кроме точки (0; 0), расположены выше оси х ." width="640"