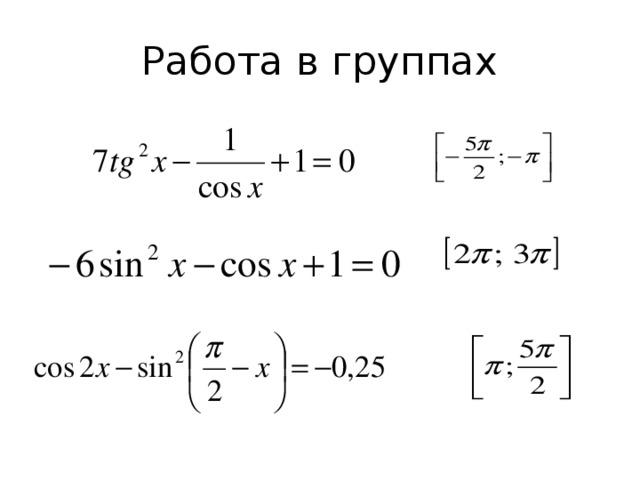Методическая разработка урока "Решение уравнений, составленных на основе материалов ЕГЭ по математике". Алгебра и начала анализа. 10 класс
Цель урока:
Систематизация и углубление знаний учащихся по теме «Решение тригонометрических уравнений с выбором корней на промежутке».
Задачи урока:
- образовательные:
- выявить качество и уровень овладения знаниями и умениями, полученными на предыдущих уроках по теме;
- закрепить умение решать тригонометрические уравнения различными методами;
- продолжать учить находить наиболее рациональные способы выбора корней тригонометрического уравнения на промежутке.
- воспитательные:
- воспитывать настойчивость в приобретении знаний и умений, умения принимать самостоятельные решения;
- воспитывать общую культуру, эстетическое восприятие окружающего мира;
- прививать интерес к изучаемому предмету.
- развивающие:
- развивать логическое мышление через умение обобщать и систематизировать;
- продолжать учить чётко и ясно излагать свои мысли.
Развитие УУД:
- Личностные: осознавать причины успеха и неуспеха в учебной деятельности
- Регулятивные: определять цель своей учебной деятельности
- Познавательные: осуществлять выбор наиболее эффективных методов решения уравнений
- Коммуникативные: адекватно составлять речевые высказывания при проговаривании способов отбора корней уравнения на промежутке
Тип урока:
Урок – практикум (урок применения знаний и умений).
Формы урока:
- Фронтальная;
- Индивидуальная;
- Парная;
- Групповая
Оборудование урока:
Проектор, экран (интерактивная доска), презентация для сопровождения урока.
Авторский медиапродукт
I. Среда - Microsoft Office PowerPoint
II. Вид медиапродукта - наглядная презентация изучаемого учебного материала.
III. Структура презентации:
№ n/n
Структурные элементы
Временная
№ слайда
1
Организационный момент
2 минуты
1,2,3,4
2
Фронтальное решение тригонометрического уравнения с выбором корней на промежутке, используя графический способ
5 минуты
5,6,7
3
Фронтальное решение тригонометрического уравнения с выбором корней на промежутке, используя единичную окружность
5 минуты
8,9
4
Работа в парах. Решение тригонометрического уравнения с выбором корней на промежутке, используя способ оценки границ (двойное неравенство)
5 минут
10,11
5
Задания для работы в группах
12
6
Проверка работы 1 группы
4 минуты
13,14,15
7
Проверка работы 2 группы
4 минуты
16,17,18
8
Проверка работы 3 группы
4 минуты
19,20,21
7
Подведение итогов урока
5 минуты
22,23
8
Задание на дом
1 минута
24
Контроль:
- Со стороны учителя: фронтальный, осуществляется при индивидуальном опросе обучающихся в течение урока. Оценка учителем итогового результата.
- Со стороны обучающихся: самоконтроль, взаимный контроль при работе в парах и группах.
Ход урока:
Этап
урока (деятельность учителя)
Содержание
1.
Организационный момент (Проверка готовности обучающихся, их настроя на работу)
Здравствуйте, ребята. Девизом нашего сегодняшнего урока я выбрал слова известного французского писателя «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом»
Анатоль Франс
(1844-1924)
.
Еще в древности одним из важнейших достоинств человека считали владение математическими знаниями. Мы начинаем урок алгебры.
2. Формулировка темы, цели, задач урока и мотивация (Подведение детей к формулированию задач урока. Составление плана работы)
Тема сегодняшнего урока:
«Решение тригонометрических уравнений с выбором корней на промежутке» (Попросить обучающихся сформулировать цель урока)
Сегодня на уроке мы с вами систематизируем, углубим знания и продолжим формировать умение решать тригонометрические уравнения.
А для этого мы вспомним все известные вам методы решения уравнений. Давайте проанализируем следующие слова:
«Метод решения хорош тем, что если с самого начала мы можем предвидеть и впоследствии подтвердить это, то, следуя этому, мы достигнем цели»
Вильгельм Лейбниц
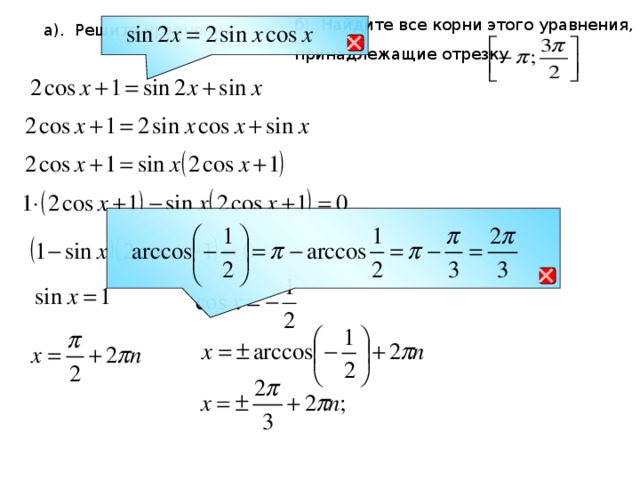
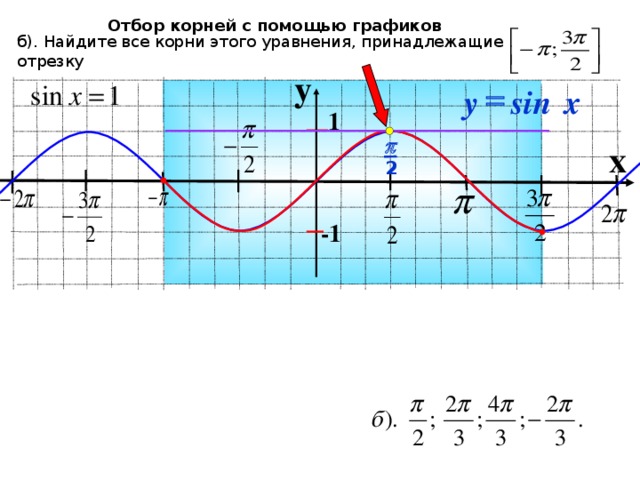
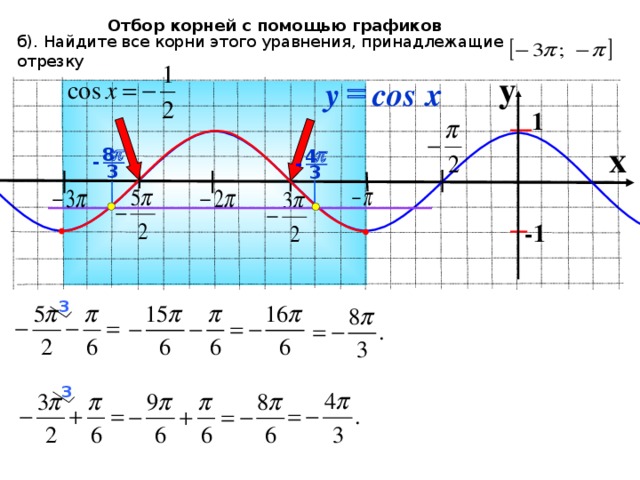
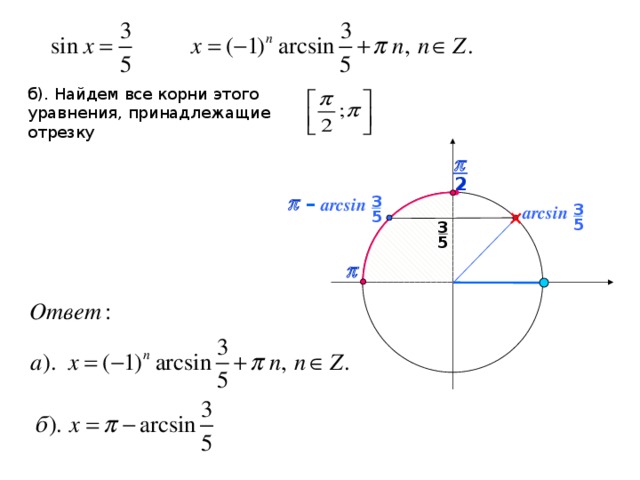
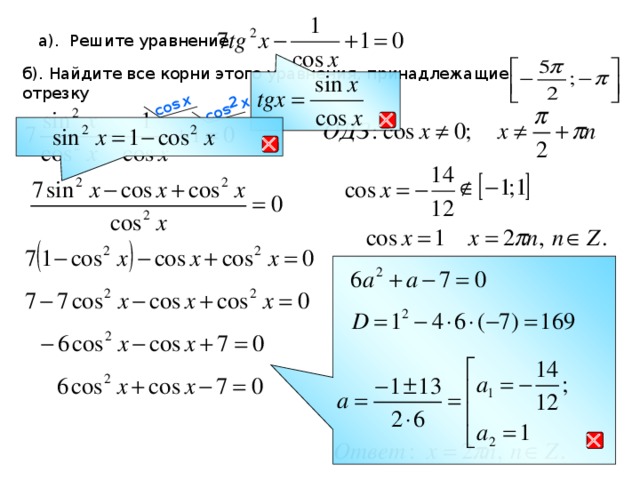
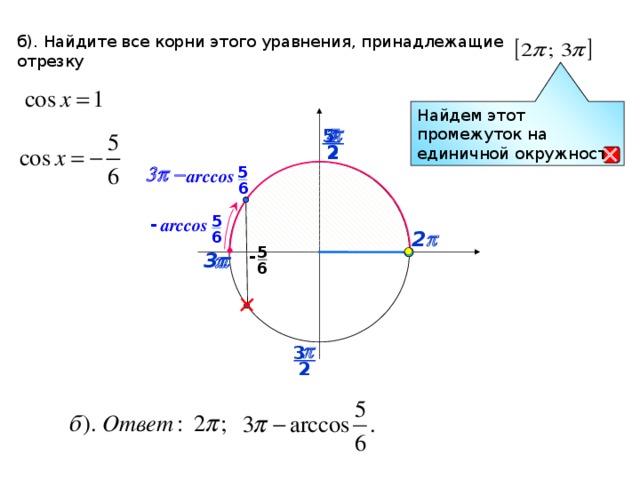
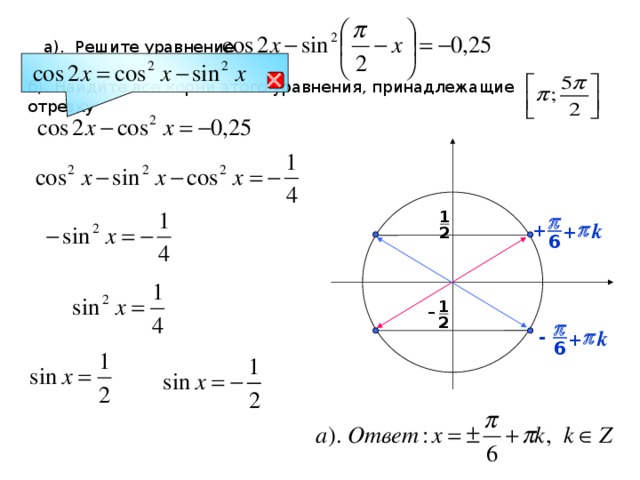
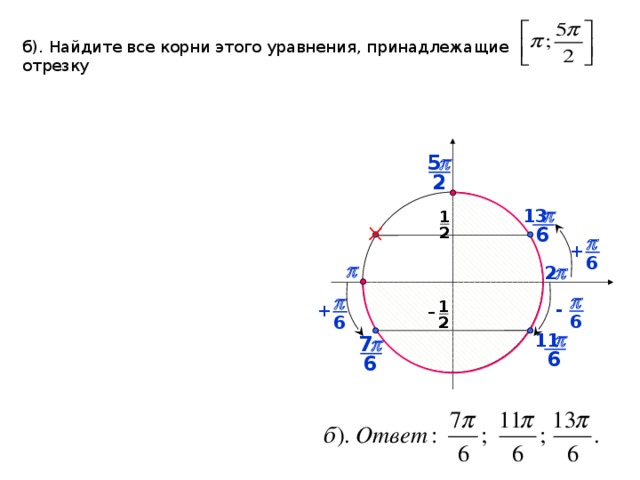
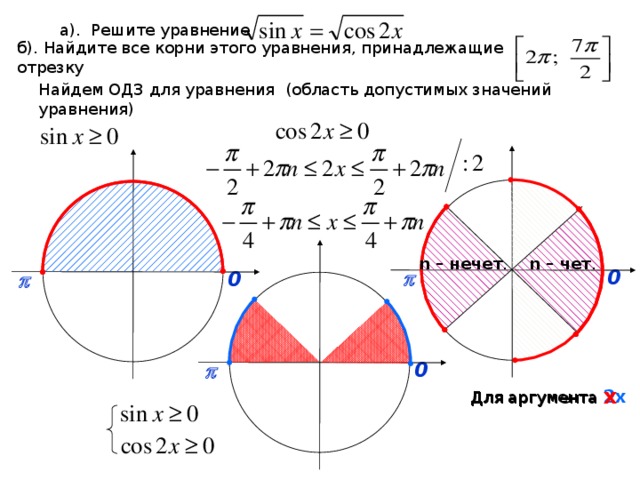
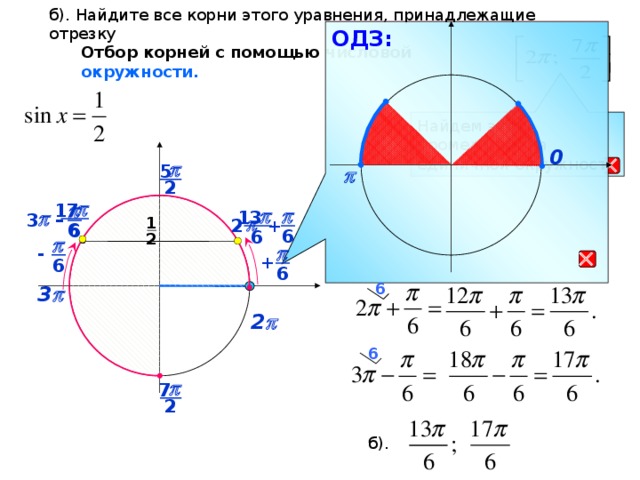
3. Фронтальное решение уравнений (Организация обсуждения решений уравнений)
1) на промежутке
2)
на промежутке
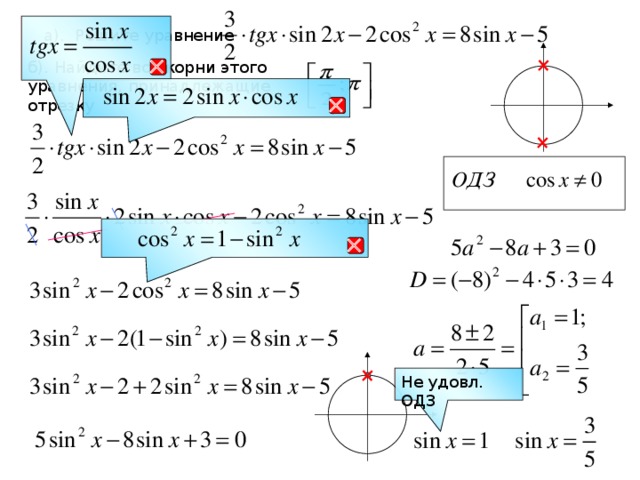
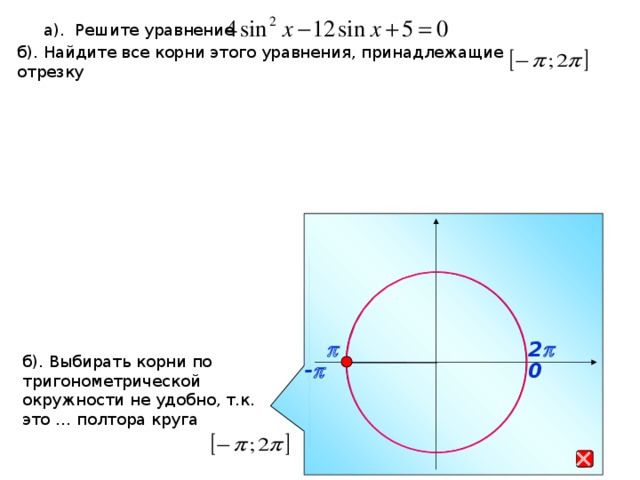
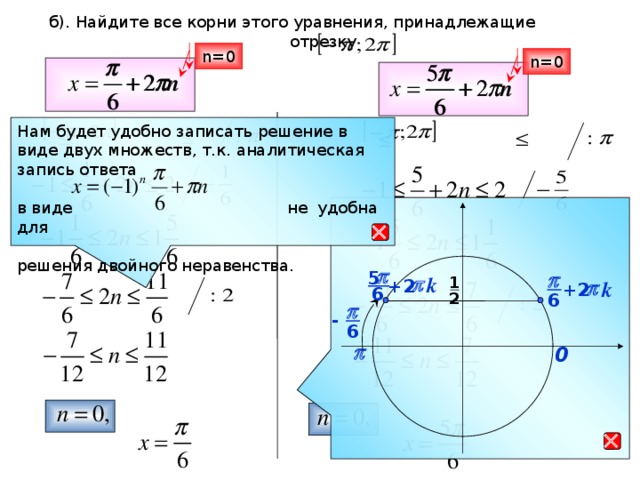
4. Работа в парах с последующей проверкой решения на доске (Организация подводящего диалога)
Решить уравнение: на промежутке
Удобно ли отобрать корни с помощью единичной окружности? Почему?
Какой способ отбора корней удобнее применить? (оценка границ)
5. Работа в группах с последующей защитой решения каждой группы на доске (Организация деления класса на группы. Регулирование работы групп, по мере необходимости помощь в выполнении задания)
1 группа:
2 группа:
3 группа:
7. Подведение итогов, рефлексия (Соотнесение поставленных задач с достигнутым результатом, постановка дальнейших целей)
Решение тригонометрического уравнения с последующим выбором корней из заданного промежутка эксперты оценивают выполнение задания по следующим критериям:
- обоснованно получены ответы в обоих пунктах – 2 балла (это макс. балл);
- обосновано решение в пункте а или б –
1 балл;
- решение не соответствует ни одному из критериев, перечисленных выше – 0 баллов
Учитель: -Продолжите предложения:
- Я сегодня повторил (а)….
- Мне сегодня понравилось…
- Я сегодня научился (ась)…
8. Домашнее задание (Объясняет сущность домашнего задания)
Решить уравнение: на промежутке
Учитель: -Закончить наш урок хочется словами известного учёного:
«Вы - талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много вы сумеете, если будете постоянно работать над собой…»
Жан-Жак Руссо
Урок окончен! Всего вам доброго! Спасибо за урок.
Литература, использованная при подготовке к уроку:
1. Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: В двух частях. Ч. 1: Учеб. для общеобразоват. учреждений. – 4-е изд. – М.: Мнемозина, 2011. – 375 с.: ил.
2. Алгебра и начала анализа. 10-11 кл.: В двух частях. Ч. 2: Задачник для общеобразоват. учреждений. Под ред. А.Г. Мордковича. - 4-е изд. – М.: Мнемозина, 2011. – 315 с.: ил.
3. Глазков Ю.А., Варшавский И.К., Гаиашвили М.Я. Математика. Решение задач группы С. – 2 изд., перераб. и доп. – М.: Издательство «Экзамен», 2009. – 382 с. (Серия «ЕГЭ. 100 баллов»).