~~Задачи урока «Неравенства с одной переменной», презентация к которому представлена,
- обобщить теоретические знания учащихся по теме «Неравенства»;
- рассмотреть решение задач, связанных с этой темой,
- организовать работу учащихся по теме урока на уровне, соответствующем уровню уже сформированных у них знаний
- закрепить умения и навыки:
• изображать на координатной прямой числовые промежутки;
• записывать их обозначения;
• решать неравенства с одной переменной.
Преподавание ведется по учебнику Алгебра 8 автор Виленкин.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Презентация к уроку по теме: "Неравенства с одной переменной"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к уроку по теме: "Неравенства с одной переменной" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1650 руб.
2350 руб.
1670 руб.
2380 руб.
1680 руб.
2400 руб.
1670 руб.
2380 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


 a (a;∞) луч x≥a [a;∞) открытый луч x (-∞;b) луч x≤b (-∞;b] ////////////////// а b ////////////////// а b /////////////////// а b /////////////////// а b //////////////////////////// а Можно использовать для объяснения как нового материала, так и для повторения на последующих уроках, используя интерактивную доску или просто устный опрос. //////////////////////////// а ///////////////////////////// b ////////////////////////////// b 3" width="640"
a (a;∞) луч x≥a [a;∞) открытый луч x (-∞;b) луч x≤b (-∞;b] ////////////////// а b ////////////////// а b /////////////////// а b /////////////////// а b //////////////////////////// а Можно использовать для объяснения как нового материала, так и для повторения на последующих уроках, используя интерактивную доску или просто устный опрос. //////////////////////////// а ///////////////////////////// b ////////////////////////////// b 3" width="640"
 –4. б) x ≤ 6 ." width="640"
–4. б) x ≤ 6 ." width="640"
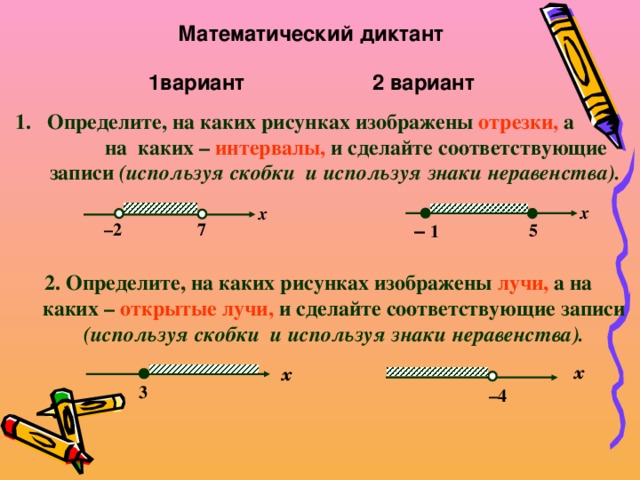
![Проверьте себя: 2 вариант 1вариант 1. Определите, на каких рисунках изображены отрезки, а на каких – интервалы, и сделайте соответствующие записи (используя скобки и используя знаки неравенства). x x – 1 7 – 2 5 – 1 ≤ x ≤ 5. интервал ( – 2; 7 ) , отрезок [– 1; 5], – 2 7. 2. Определите, на каких рисунках изображены лучи, а на каких – открытые лучи, и сделайте соответствующие записи (используя скобки и используя знаки неравенства). x x 3 – 4 луч [3; +∞ ), x ≥ 3 . открытый луч (– ∞ ; – 4 ), x 4 .](https://fsd.kopilkaurokov.ru/uploads/user_file_53fda06f7ac03/img_user_file_53fda06f7ac03_5.jpg)
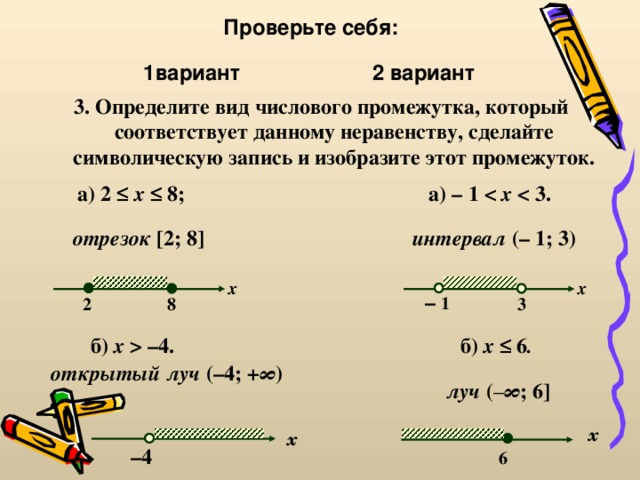 –4. открытый луч (–4; +∞ ) луч ( – ∞ ; 6] x x – 4 6" width="640"
–4. открытый луч (–4; +∞ ) луч ( – ∞ ; 6] x x – 4 6" width="640"


 0 Значит, х=3 не является решением данного неравенства При х=-5, 4∙(-5)=-15, -15 Значит, х=-5 является решением данного неравенства" width="640"
0 Значит, х=3 не является решением данного неравенства При х=-5, 4∙(-5)=-15, -15 Значит, х=-5 является решением данного неравенства" width="640"
 4х ( :4) 2х – 3 х" width="640"
4х ( :4) 2х – 3 х" width="640"
 на Например : а) - 6х + – 15 0 (: (-3)) 2х + 5 0" width="640"
на Например : а) - 6х + – 15 0 (: (-3)) 2х + 5 0" width="640"
 13х+45" width="640"
13х+45" width="640"
 13х - 1 Решение : 5х + 6х – 3 13х – 1 5х + 6х – 13х 3 – 1 -2х 2 (: (-2)) х \\\\\\\\\ Ответ: (-∞; -1) -1" width="640"
13х - 1 Решение : 5х + 6х – 3 13х – 1 5х + 6х – 13х 3 – 1 -2х 2 (: (-2)) х \\\\\\\\\ Ответ: (-∞; -1) -1" width="640"


![Ответы к самостоятельной: 1 вариант : a) [9;∞) b) (-∞;-4) c) (-∞;0,5] d) (-∞;9) 2 вариант: a) (-∞;7] b) (7;∞) c)[0,25;∞) d) (10;∞)](https://fsd.kopilkaurokov.ru/uploads/user_file_53fda06f7ac03/img_user_file_53fda06f7ac03_16.jpg)

 b . Умножив обе части неравенства на b – а , получим: а ( b – а) b ( b – а). Продолжим преобразования. ab – a 2 b 2 -ab ab – a 2 –b 2 + ab 0 – a 2 + 2ab – b 2 0 a 2 - 2ab + b 2 (a – b) 2 0 Итак, мы доказали, что всякое положительное число меньше нуля." width="640"
b . Умножив обе части неравенства на b – а , получим: а ( b – а) b ( b – а). Продолжим преобразования. ab – a 2 b 2 -ab ab – a 2 –b 2 + ab 0 – a 2 + 2ab – b 2 0 a 2 - 2ab + b 2 (a – b) 2 0 Итак, мы доказали, что всякое положительное число меньше нуля." width="640"
 b , ( b – а) Поэтому решение должно выглядеть так: а( b – а) b ( b – а). Продолжим преобразования. ab – a 2 b 2 - ab ab – a 2 –b 2 + ab 0 – a 2 + 2ab – b 2 0 a 2 - 2ab + b 2 0 ( a – b ) 2 0 " width="640"
b , ( b – а) Поэтому решение должно выглядеть так: а( b – а) b ( b – а). Продолжим преобразования. ab – a 2 b 2 - ab ab – a 2 –b 2 + ab 0 – a 2 + 2ab – b 2 0 a 2 - 2ab + b 2 0 ( a – b ) 2 0 " width="640"
 0; в) 5(у – 1,2) – 4,6 Д/з: 1. Решите неравенство: а) х ≤ 2; б) 2 - 7х 0; в) 6(у – 1,5) – 3,4 ≤ 4у – 2,4. 2. При каких b значение дроби больше соответствующего значения дроби ?" width="640"
0; в) 5(у – 1,2) – 4,6 Д/з: 1. Решите неравенство: а) х ≤ 2; б) 2 - 7х 0; в) 6(у – 1,5) – 3,4 ≤ 4у – 2,4. 2. При каких b значение дроби больше соответствующего значения дроби ?" width="640"





















