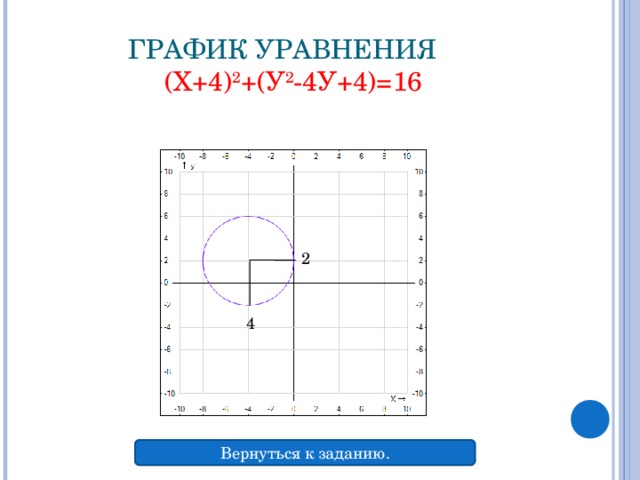
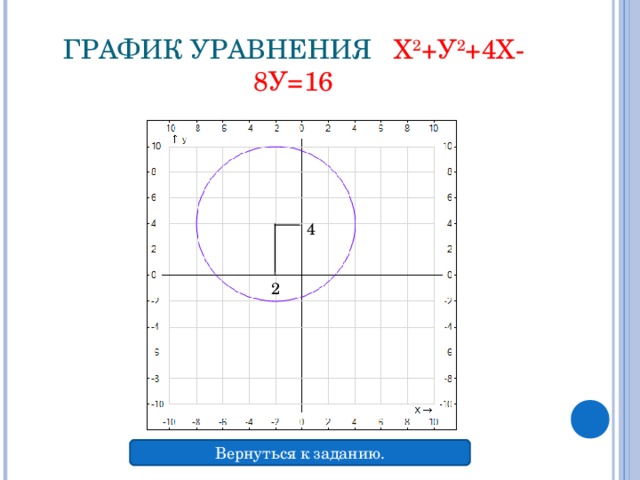
УРАВНЕНИЕ ОКРУЖНОСТИ
1 ЭТАП: ВЫВОД ФОРМУЛЫ
Уравнение фигуры – это уравнениес двумя переменными х и у, которомуудовлетворяют координаты любойточки фигуры.Пусть дана окружность.А(а;b) – центр окружности, С(х ; у) – точка окружности, М(х; у) – точка окружности.Что можно сказать о взаимном расположении точек А и С на плоскости и точек А и М на плоскости?Как можно сформулировать определение окружности?
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
ВЫВОД ФОРМУЛЫ
Пусть дана окружность.А(а;b) – центр окружности, С(х ; у) – точка окружности. Найти расстояние между точками А с С.d 2 = АС 2 = (х – а)2 + (у – b)2, Как можно назвать отрезок АС?d = АС = R, следовательноR 2 = (х – а)2 + (у – b)2
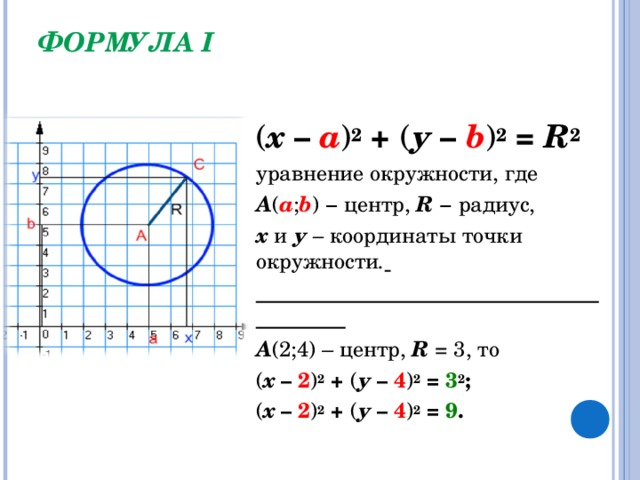
ФОРМУЛА I
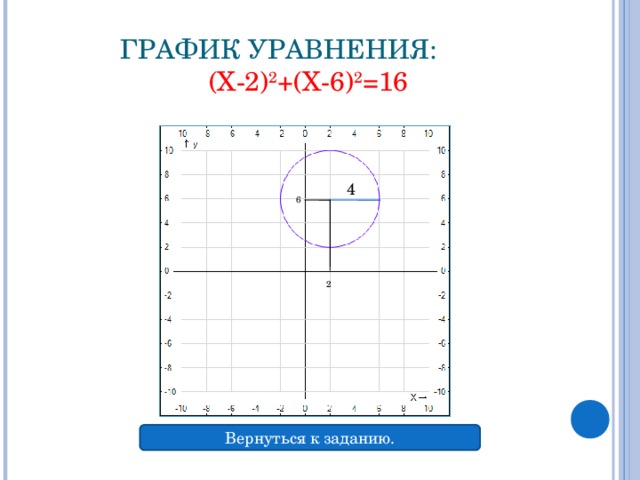
(х – а)2 + (у – b)2 = R2уравнение окружности, гдеА(а;b) − центр, R − радиус,х и у – координаты точки окружности. __________________________ А(2;4) – центр, R = 3, то(х – 2)2 + (у – 4)2 = 32;(х – 2)2 + (у – 4)2 = 9.
ФОРМУЛА II
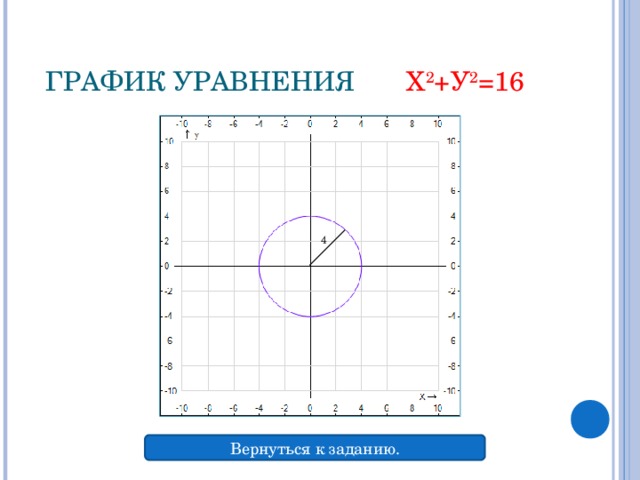
(х – а)2 + (у – b)2 = R 2 .Центр окружности О(0;0), (х – 0)2 + (у – 0)2 = R 2,х2 + у2 = R 2 − уравнение окружности с центром в начале координат. . О (0;0) – центр, R = 5, тогдах2 + у2 = 52;х2 + у2 = 25.
ДЛЯ ТОГО ЧТОБЫ СОСТАВИТЬ УРАВНЕНИЕОКРУЖНОСТИ, НУЖНО:
1) узнать координаты центра;2) узнать длину радиуса;3) подставить координаты центра (а;b) и длину радиуса R в уравнение окружности(х – а)2 + (у – b)2 = R2.
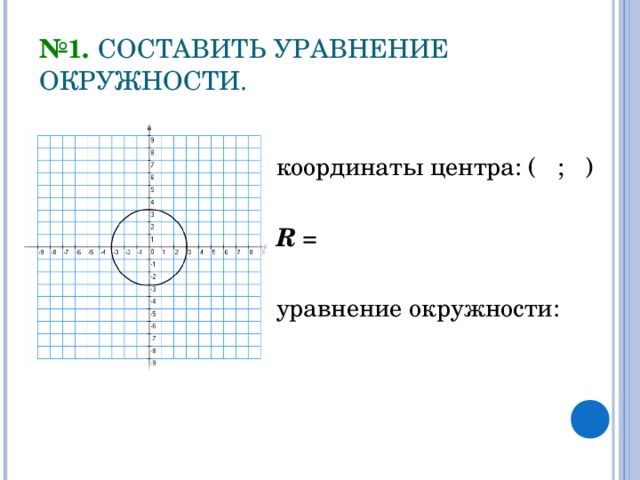
№1. СОСТАВИТЬ УРАВНЕНИЕ ОКРУЖНОСТИ.
координаты центра: ( ; )R = уравнение окружности:
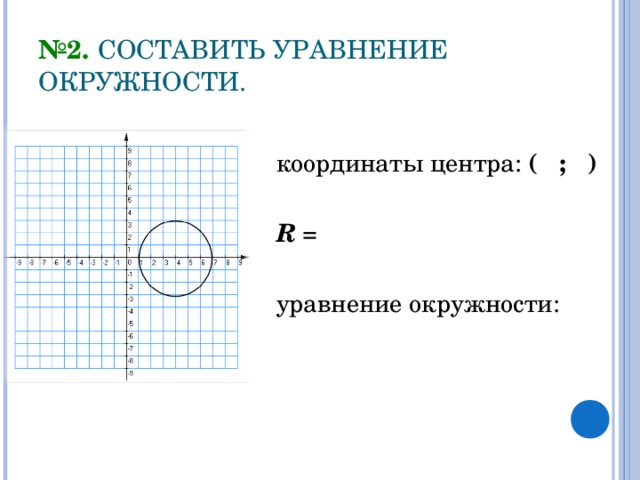
№2. СОСТАВИТЬ УРАВНЕНИЕ ОКРУЖНОСТИ.
координаты центра: ( ; )R = уравнение окружности:
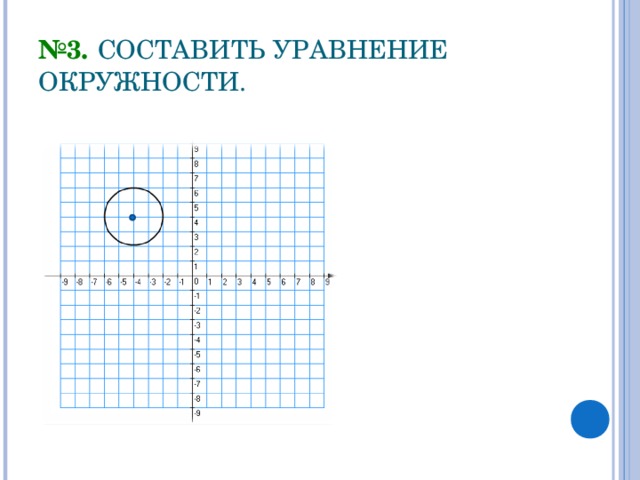
№3. СОСТАВИТЬ УРАВНЕНИЕ ОКРУЖНОСТИ.
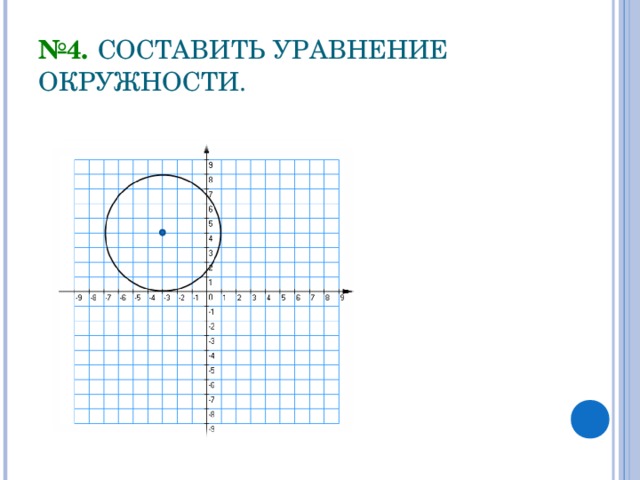
№4. СОСТАВИТЬ УРАВНЕНИЕ ОКРУЖНОСТИ.
№2. ПОСТРОЙТЕ В ТЕТРАДИ ОКРУЖНОСТИ, ЗАДАННЫЕ УРАВНЕНИЯМИ:
(х – 5)2 + (у + 3)2 = 36;2) (х + 1)2 + (у – 7)2 = 49.
Вернуться к групповым заданиям
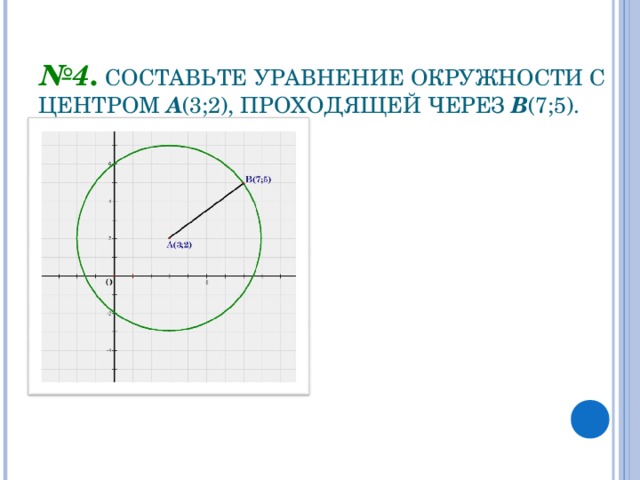
№4. СОСТАВЬТЕ УРАВНЕНИЕ ОКРУЖНОСТИ С ЦЕНТРОМ А(3;2), ПРОХОДЯЩЕЙ ЧЕРЕЗ В(7;5).
ГРУППА2: №1 НАЙДИТЕ КООРДИНАТЫ ЦЕНТРА И РАДИУС, ЕСЛИ АВ – ДИАМЕТР ДАННОЙ ОКРУЖНОСТИ.
Дано
Радиус
Координаты центра
А(0;−6)В(0; 2)
d 2= (x2 – x1)2 + (y2 – y1)2СВ 2=R 2=R 2=R =
А (0; −6)В (0; 2) .С ( ; )-середина АВС ( ; )
А(−2;0)В( 4; 0)
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Презентация к уроку "Уравнение окружности" 9 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к уроку "Уравнение окружности" 9 класс »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1850 руб.
2640 руб.
1750 руб.
2500 руб.
1850 руб.
2640 руб.
1460 руб.
2090 руб.
Курсы ПК и ППК для учителей!
500 руб.
2500 руб.
800 руб.
4000 руб.
600 руб.
3000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства