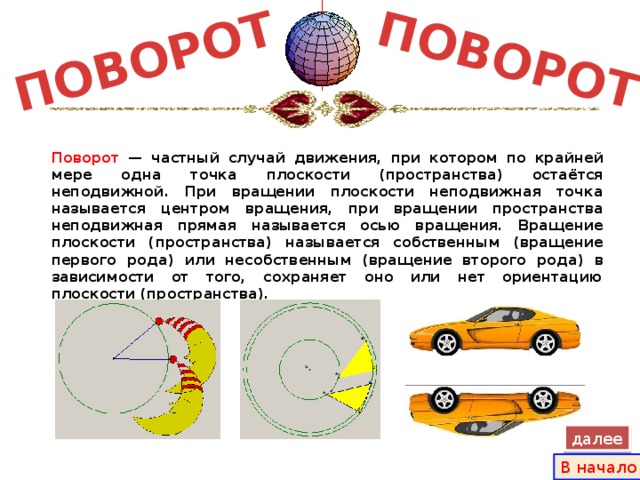
Презентация по геометрии подготовлена учеником 9 класса Проноза Владиславом. Идет пояснение смысла термина о "движении" и идет описание некоторых его видов. Показывается несколько видов движения по выделению симметрии, параллельный перенос и поворот объекта.
Симметрия О симметрия! Гимн тебе пою!Тебя повсюду в мире узнаюТы в Эйфелевой башне, в малой мошке,Ты в елочке, что у лесной дорожки.С тобою в дружбе и тюльпан и розаИ снежный рай – творение мороза.
Этот материал можно использовать как для изучения новой темы, так и для повторения и обобщения.