Цели урока:
?формирование и первичная отработка понятий “функция”, “аргумент функции”, “значение функции”, “независимая переменная”, “зависимая переменная”;
?формирование представлений о способах задания функций;
?начать выработку умений строить и читать графики функций;
?отработка умений решения простейших задач, опираясь на графики и таблицы;
формировать у учащихся познавательный интерес к алгебре.
Просмотр содержимого документа
«Презентация по теме "Что такое функция" »

Что такое функция?
7 класс
Первый урок по теме «Функции»
Составила учитель математики
МБОУ «Козловская СОШ» Науенова А.Р.

Цели урока:
- формирование и первичная отработка понятий “функция”, “аргумент функции”, “значение функции”, “независимая переменная”, “зависимая переменная”;
- формирование представлений о способах задания функций;
- начать выработку умений строить и читать графики функций;
- отработка умений решения простейших задач, опираясь на графики и таблицы;
- формировать у учащихся познавательный интерес к алгебре.

Устный счёт
х =
х =
х =
х =
х =
х =
- 12 ТЬ
- 0,9 ВИ
- 0,8 ЗА
- 4 МО
0,25 С
20 СИ

Ключевое слово урока:
зависимость
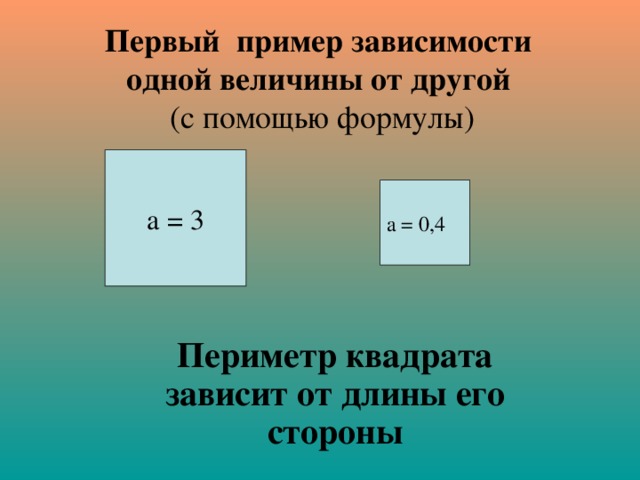
Первый пример зависимости одной величины от другой (с помощью формулы)
а = 3
а = 0,4
Периметр квадрата зависит от длины его стороны

R = 5 см
R = 2 см
Длина окружности зависит от длины её радиуса

V = 30 км/ч
V = 6 0 км/ч
Пройденный путь зависит от его скорости

Описание зависимостей с помощью формул
- Р = 4 а ( р зависит от а)
- С =2п R ( с зависит от R )
- S = t v ( s зависит от v )
Если переменные а, R , v обозначить буквой х, а переменные P , C , S обозначить буквой у, то получатся формулы звисимостей у от х .

Р (периметр квадрата)
Функция
а (длина стороны)
Зависимая переменная
Аргумент функции
Независимая переменная

Что же такое функция?
Функцией называют такую зависимость
переменной у от переменной х ,
при которой
каждому значению х
соответствует
единственное значение у

Факты из истории.
- Впервые термин «функция» ввёл И.Бернулли в 1718 году
- В общем виде определение функции было дано Н.И. Лобачевским в 1934 г.

Второй пример зависимости одной величины от другой (табличный):
В таблице показана зависимость стоимости проезда в пригородном поезде от номера зоны, к которой относится станция
х
у
1
2
10
3
15
4
20
25
5
6
40
50
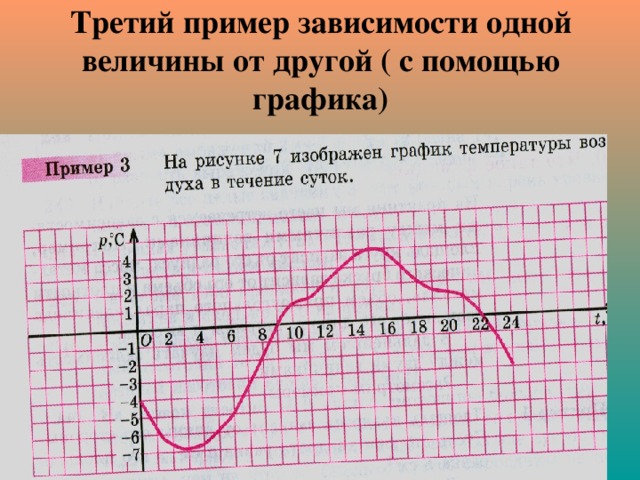
Третий пример зависимости одной величины от другой ( с помощью графика)
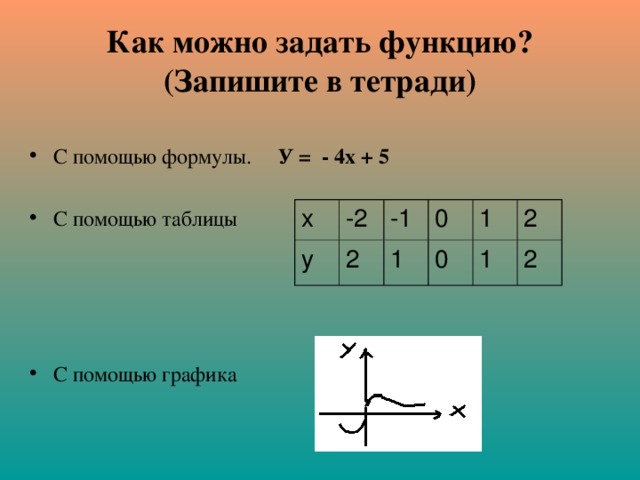
Как можно задать функцию? (Запишите в тетради)
- С помощью формулы. У = - 4х + 5
х
у
-2
2
-1
1
0
0
1
2
1
2

Работа с учебником

Домашнее задание (записать в дневники)
- Читать П 12, стр 55 – 57 ( до последнего определения), выучить определение функции и значения новых терминов
- № 259, № 262,№ 266
- Желающие находят дополнительный материал по теме «История появления понятия «функция»

Дайте ответы на вопросы .
- Как вы поняли, что такое функция?
- Приведите два примера зависимости одной величины от другой
- Какими способами может быть задана функция?
- Как иначе можно назвать независимую переменную ?
- Как иначе можно назвать зависимую переменную?