Презентация "Приемы устного счета"

Научный проект на тему:

Научный руководитель: учитель математики Малкандуева Л.М

Автор проекта: Карачаева Алина

учени ца 5 «В» класса

МОУ «Гимназия №14»

Как считать быстро и правильно?

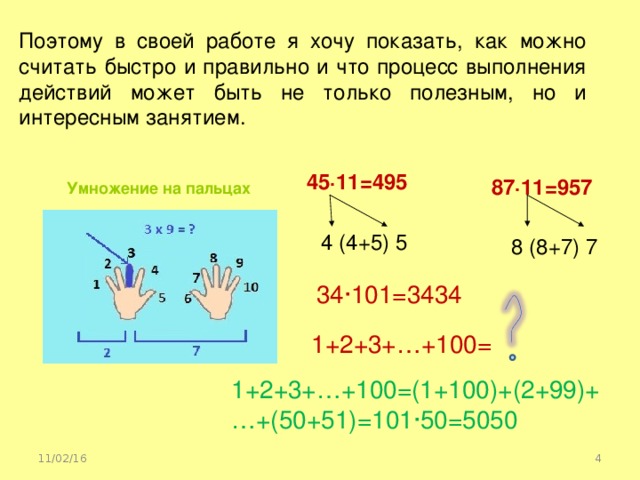
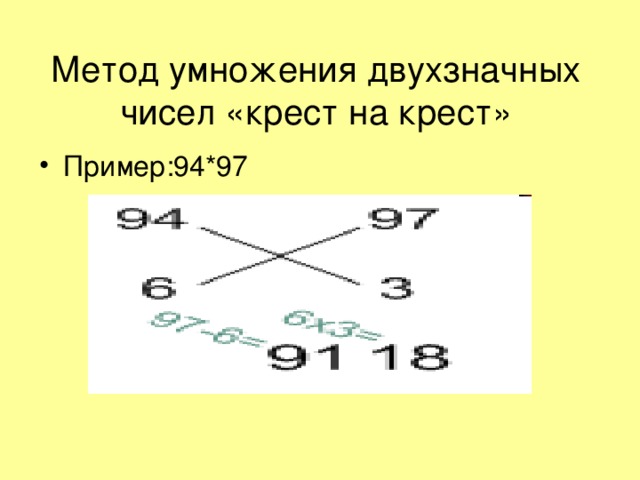
Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь

с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться

считать.

11/02/16

Актуальность моего исследования состоит в том,

что в наше время все чаще на помощь ученикам приходят калькуляторы, и все большее количество учеников не может считать устно.

А ведь изучение математики развивает логическое мышление, память, гибкость ума, приучает человека

к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека.

Поэтому в своей работе я хочу показать, как можно считать быстро и правильно и что процесс выполнения действий может быть не только полезным, но и интересным занятием.

45∙11=495

87∙11=957

Умножение на пальцах

4 (4+5) 5

8 (8+7) 7

34∙101=3434

1+2+3+…+100=

1+2+3+…+100=(1+100)+(2+99)+…+(50+51)=101∙50=5050

11/02/16

Цель: изучить приемы быстрого счета, показать необходимость их применения для упрощения вычислений.

В соответствии с поставленной целью были определены задачи :

• Исследовать, применяют ли школьники приемы быстрого счета.
• Изучить приемы быстрого счета, которые можно

использовать, упрощая вычисления.

• Составить памятку для учащихся 5-6 классов для

применения приемов быстрого счета.

Объект исследования : приемы быстрого счета.

Предмет исследования : процесс вычислений.

11/02/16

4

Гипотеза исследования : если показать, что применение приемов быстрого счета, облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и им будет легче решать практические задачи.

При выполнении работы были использованы следующие приемы и методы : опрос (анкетирование), анализ (статистическая обработка данных), работа с источниками информации, практическая работа, наблюдения.

11/02/16

Анкета

1 . Зачем нужно уметь считать?

а) пригодится в жизни, например, считать деньги;

б) чтобы хорошо учиться в школе; в) чтобы быстро решать;

г) чтобы быть грамотным; д) не обязательно уметь считать.

2. Перечисли, при изучении каких школьных предметов тебе понадобится правильно считать?

а) математика; б) физика; в) химия; г) технология; д) музыка; е) физическая культура;

ж) ОБЖ; з) информатика; и) география; к) русский язык; л) литература.

3. Знаешь ли ты приемы быстрого счета?

а) да, много; б) да, несколько; в) нет, не знаю.

4. Применяешь ли ты при вычислениях приемы быстрого счета?

а) да; б) нет.

5. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?

а) да; б) нет.

11/02/16

Сбор и статистическая обработка данных

1) Зачем нужно уметь считать ?

2) При изучении каких школьных предметов тебе понадобится правильно считать?

11/02/16

3) Знаешь ли ты приёмы быстрого счёта?

4) Применяешь ли ты приёмы быстрого счёта?

5) Хотели бы вы узнать приёмы быстрого счёта, чтобы быстро решать?

11/02/16

11/02/16

Движение пальца

С помощью пальцев рук запомнить таблицу умножения на 9 .

Положив обе руки рядом на стол, по порядку занумеруем пальцы

обеих рук следующим образом: первый палец слева обозначим 1,

второй за ним обозначим цифрой 2, затем 3, 4… до десятого пальца,

который означает 10.

Если надо умножить на 9 любое

из первых девяти чисел, то для этого,

не двигая рук со стола, надо приподнять в

верх тот палец, номер которого означает

число, на которое умножается девять;

тогда число пальцев, лежащих налево

от поднятого пальца, определяет число

десятков, а число пальцев, лежащих справа

от поднятого пальца, обозначает число единиц полученного

произведения (убедитесь в этом самостоятельно).

УМНОЖЕНИЕ НА ПАЛЬЦАХ

Умножали на пальцах однозначные числа от 6 до 9.

Для этого на одной руке вытягивали столько

пальцев, насколько первый множитель превосходил

число 5,а на второй делали то же самое для второго

множителя. Остальные пальцы

загибали. После этого брали

столько десятков, сколько вытянуто

пальцев на обеих руках, и прибавляли

к этому числу произведение загнутых

пальцев на первой и второй руке.

• Пример: 8 ∙ 9 = 72

Умножение и деление на 5, 25, 50

• 1. 48 *5=48*10/2= 240
• 2. 48*25=48*100/4= 1200
• 3. 48*50=48*100/2= 2400
• 4. 725/5=725*2/10= 145
• 5. 725/25=725*4/100= 29
• 6. 1250/50=1250*2/100= 25

1. 97+44+89

100+44+100-3-11

244-14= 230

2. 98+58

100-2+60-2

160-4= 156

3. 198+52

200-2+50+2

200+50= 250

• 1. 97+44+89 100+44+100-3-11 244-14= 230 2. 98+58 100-2+60-2 160-4= 156 3. 198+52 200-2+50+2 200+50= 250
• 1. 97+44+89 100+44+100-3-11 244-14= 230 2. 98+58 100-2+60-2 160-4= 156 3. 198+52 200-2+50+2 200+50= 250
• 1. 97+44+89 100+44+100-3-11 244-14= 230 2. 98+58 100-2+60-2 160-4= 156 3. 198+52 200-2+50+2 200+50= 250
• 1. 97+44+89 100+44+100-3-11 244-14= 230 2. 98+58 100-2+60-2 160-4= 156 3. 198+52 200-2+50+2 200+50= 250

18+52+65+35+37=(18+52)+(65+35)+37=

=70+100+37=(70+37)+100=107+100= 207

• Например: 14*11= 1 5 4

Умножение на 11

• Чтобы умножить любое число на 11, к нему приписывают ноль и прибавляют исходное число.
• Например: 241*11= 241 0 + 241 =2651

• Правило: добавь цифру к ее соседу.

Под соседом подразумевается цифра справа.

Пример: 0,3425* 11=3 ,7675

0,3425 * 11=(0+3),(3+4)(4+2)(2+5)(5+0)=3,7675

Доказательство:

11=10+1

Таким образом:

3425 * 11=3425 * (10+1)=34250+3425=37675.

Умножение на 1,5

• Чтобы умножить число на 1,5, нужно к исходному числу прибавить

его половину.

• Например: 34 *1,5= 34 + 17 =51

129 *1,5= 129 + 64,5 =193,5

Возведение в квадрат

• Чтобы возвести в квадрат число, оканчивающееся цифрой 5, умножают число его десятков на число десятков, увеличенное на 1, и к полученному числу приписывают 25.
• Например: 9 5 2 = 90 25

9*10

Метод умножения двухзначных чисел «крест на крест»

Русский способ умножения 2-х чисел

• Способ этот, не похожий на наши школьные приемы, употребителен в обиходе великорусских крестьян и унаследован ими от глубокой древности. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа.
• Вот пример:
• 32 Х 13
• 16 X 26
• 8 Х 52
• 4 Х 104
• 2 X 208
• 1 X 416

Русский способ умножения 2-х чисел

• Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение:
• 32 X 13 = 1 X 416.

Русский способ умножения 2-х чисел

• Однако как поступить, если при этом приходится делить пополам число нечетное?
• Народный способ легко выводит из этого затруднения. Надо - гласит правило - в случае нечетного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца; сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
• 19 X 17
• 9 X 34
• 4 X 68*
• 2 X 136*
• 1 X 272

Русский способ умножения 2-х чисел

• Сложив незачеркнутые числа, получаем вполне правильный результат:
• 17 + 34 + 272 = 323.
• На чем основан этот прием?
• Обоснованность приема станет ясна, если принять во внимание, что
• 19 Х 17 = (18 + 1)17 = 18 X 17 + 17,
• 9 X 34 = (8 + 1)34 = 8 X 34 + 34 и т. д.
• Ясно, что числа 17, 34 и т. п., утрачиваемые при делении нечетного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение

11/02/16

Выводы:

• Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.
• В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – памятка для быстрого счета будет очень полезной для учащихся

5-6 классов.

11/02/16