Тема урока: Графическое решение квадратных уравнений.
Цели урока:
Образовательные : повторить графики ранее изученных функций, научить учащихся решать квадратные уравнения графическим способом.
Развивающие : развивать логическое мышление, познавательную и мыслительную деятельность, учить анализировать, выделять главное, сравнивать.
Воспитательные : воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.
Просмотр содержимого документа
«презентация для урока:"Графическое решение квадратных уравнений"»
ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
МБОУ Дорогобужская СОШ №2
Баринова Е.А.
Вопросы:
1. Что является графиком функции у=х+3 ?
Ответ : графиком функции у=х+3 является прямая.
2. Какая кривая является графиком функции у=0,5х 2 ?
Ответ : графиком функции у=0,5х 2 является парабола.
3 . Куда направлены ветви параболы? Почему?
Ответ : ветви параболы направлены вверх, т.к. а 0, а=0,5.
4. Что является графиком функции у=6/х ?
Ответ : графиком данной функции является гипербола.
5. В каких четвертях расположены ветви гиперболы у=- ?
Ответ : ветви гиперболы расположены во 2 и 4 четвертях.
6. Что является графиком функции у=
Ответ : ветвь параболы.
7. В каких четвертях расположен график функции у= ?
Ответ : в 3 и в 4 координатных четвертях.
8. Найти координаты вершины параболы (х 0 ;у 0 ), заданной формулой у=х 2 +2х-3 .
Ответ : х 0 =-2:2=-1.у 0 =(-1) 2 -2-3=-4,то есть (-1;-4;).
9. Какая прямая служит осью симметрии параболы: у=х 2 +2х-3 ?
Ответ : осью симметрии параболы служит прямая х=х 0 , то есть прямая х=-1 .
10 . Определите наименьшее значение функции: у=х 2 +2х-3 .
Ответ : наименьшее значение функции равно -4 .
11. Укажите промежутки возрастания и убывания функции: у=х 2 +2х-3 .
Ответ : функция у=х 2 +2х-3 убывает на промежутке (-;-1], функция возрастает на промежутке [-1;+
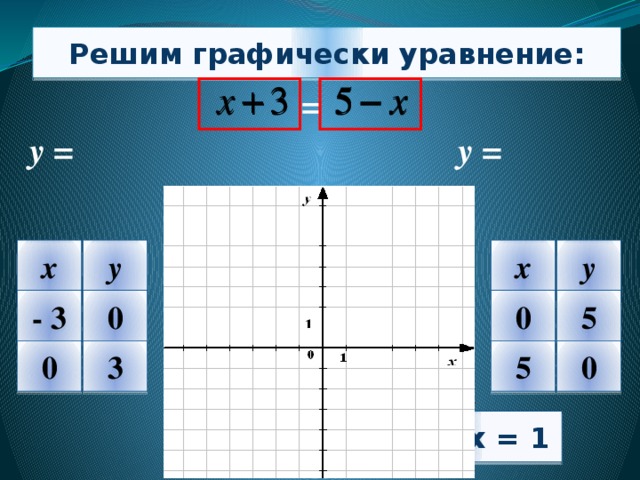
Решим графически уравнение:
=
у =
у =
х
у
х
у
- 3
0
5
0
3
0
5
0
Ответ: х = 1
Алгоритм решения:
1 . Из уравнения выделяем знакомые нам функции.
2. Строим графики функций в одной координатной плоскости.
3. Находим координаты точек пересечения графиков.
4. Из найденных координат-выбираем значение абсциссы ,то есть х.
5. Записываем ответ.
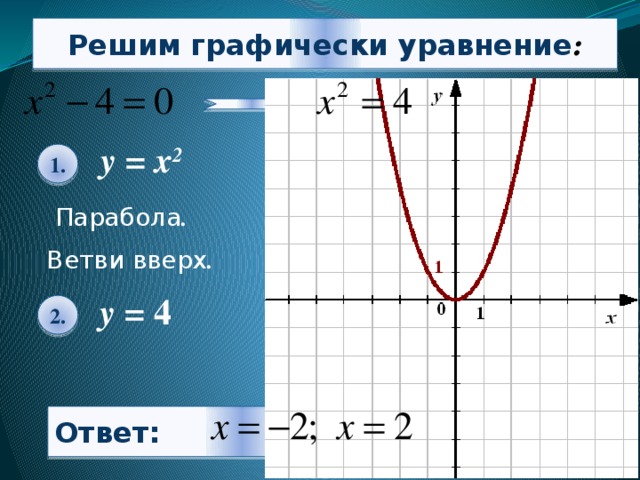
Решим графически уравнение :
у = х 2
1.
Парабола .
Ветви вверх .
у = 4
2.
-2
2
Ответ:
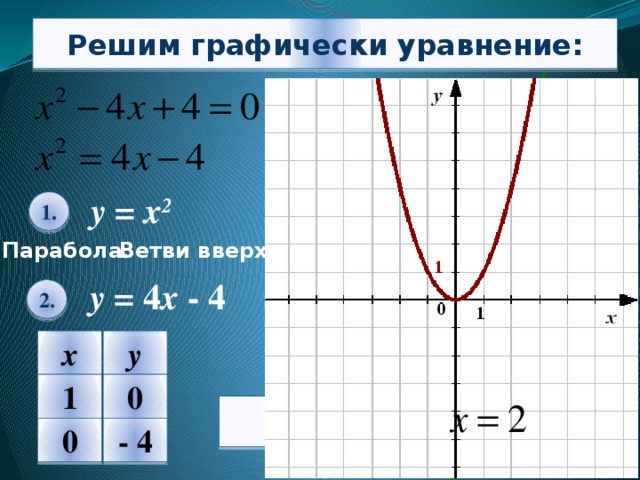
Решим графически уравнение:
у = х 2
1.
Парабола .
Ветви вверх .
у = 4 х - 4
2.
у
х
2
1
0
Ответ:
- 4
0
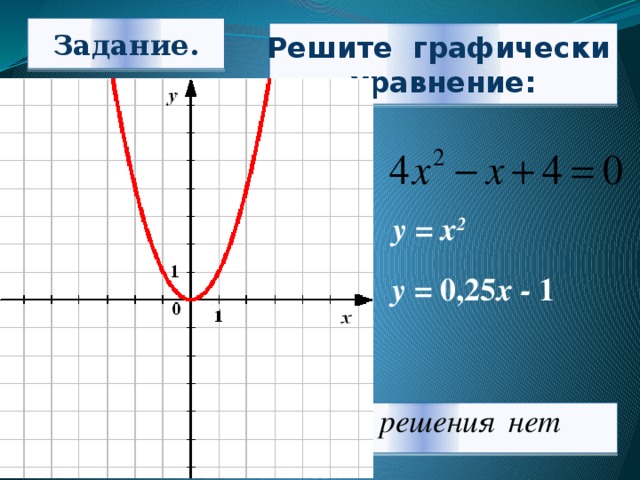
Задание.
Решите графически
уравнение:
у = х 2
у = 0,25 х - 1
Ответ:
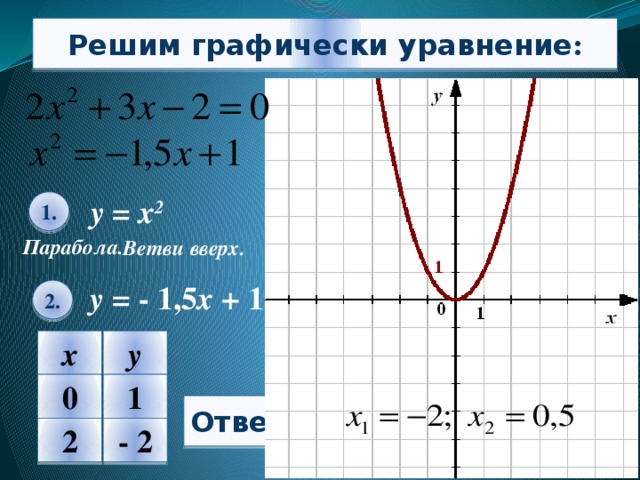
Решим графически уравнение :
у = х 2
1.
Парабола.
Ветви вверх.
у = - 1,5 х + 1
2.
х
у
-2
0,5
0
1
Ответ :
- 2
2
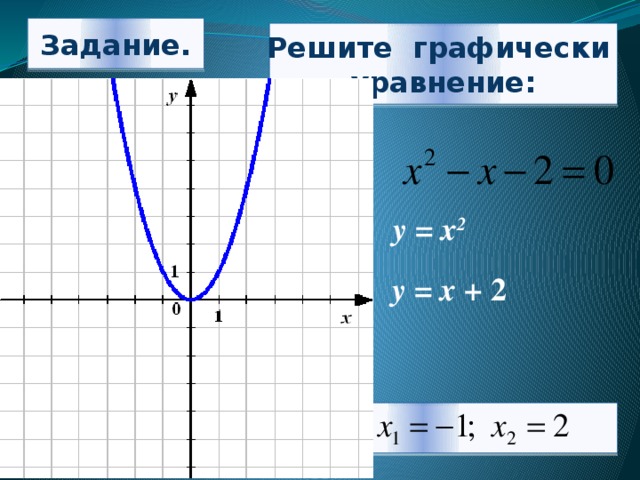
Задание.
Решите графически
уравнение:
у = х 2
у = х + 2
-1
2
Ответ:
Я - понял…
Я - знаю…
Я - умею…
решать квадратные уравнения графически.


![7. В каких четвертях расположен график функции у= ? Ответ : в 3 и в 4 координатных четвертях. 8. Найти координаты вершины параболы (х 0 ;у 0 ), заданной формулой у=х 2 +2х-3 . Ответ : х 0 =-2:2=-1.у 0 =(-1) 2 -2-3=-4,то есть (-1;-4;). 9. Какая прямая служит осью симметрии параболы: у=х 2 +2х-3 ? Ответ : осью симметрии параболы служит прямая х=х 0 , то есть прямая х=-1 . 10 . Определите наименьшее значение функции: у=х 2 +2х-3 . Ответ : наименьшее значение функции равно -4 . 11. Укажите промежутки возрастания и убывания функции: у=х 2 +2х-3 . Ответ : функция у=х 2 +2х-3 убывает на промежутке (-;-1], функция возрастает на промежутке [-1;+](https://fsd.kopilkaurokov.ru/uploads/user_file_5681a897de9ad/img_user_file_5681a897de9ad_2.jpg)