Презентация предназначена для использования на уроках матетатики в школе или средних специальных учебных заведений. В ней рассматриваются задачи, приводящие к понятию производной, определение производной, алгоритм и примеры нахождения производных некоторых элементарных функций, таблица производных. Правила вычисления производных и др.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
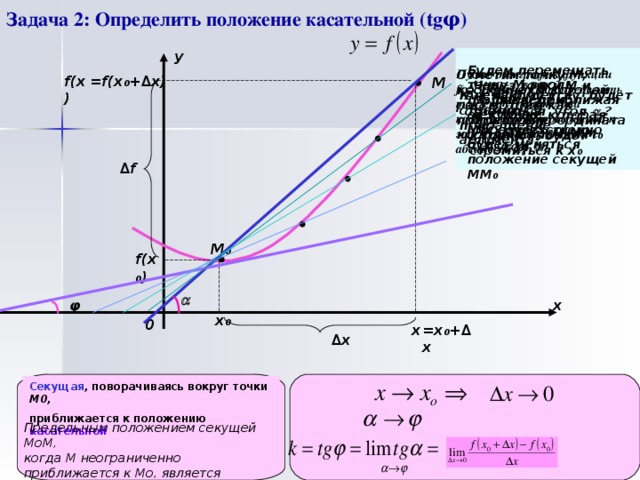
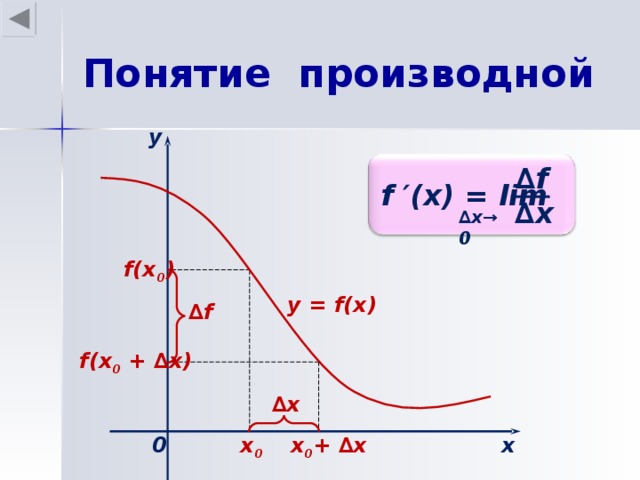
Производная. Физический и геометрический смысл производной.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Производная. Физический и геометрический смысл производной. »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1390 руб.
1980 руб.
1850 руб.
2640 руб.
1460 руб.
2090 руб.
1860 руб.
2660 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



![Задачи, приводящие к понятию производной N М О Предположим, что в начальный момент времени t тело находилось в точке M , её координата – s(t). за время t оно прошло путь М N . Координата точки N – s(t + t) . Тогда М N = s = s(t + t) – s(t) Нетрудно найти среднюю скорость движения тела за промежуток времени [ t; t+∆t] :](https://fsd.kopilkaurokov.ru/uploads/user_file_55155e1096c8c/img_user_file_55155e1096c8c_3.jpg)
![Задачи, приводящие к понятию производной А что такое скорость v (t) в момент времени t (её называют иногда мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [t; t+∆t] при условии , что ∆t выбирается все меньше и меньше; иными словами, при условии, что ∆t→0. Это значит , что](https://fsd.kopilkaurokov.ru/uploads/user_file_55155e1096c8c/img_user_file_55155e1096c8c_4.jpg)