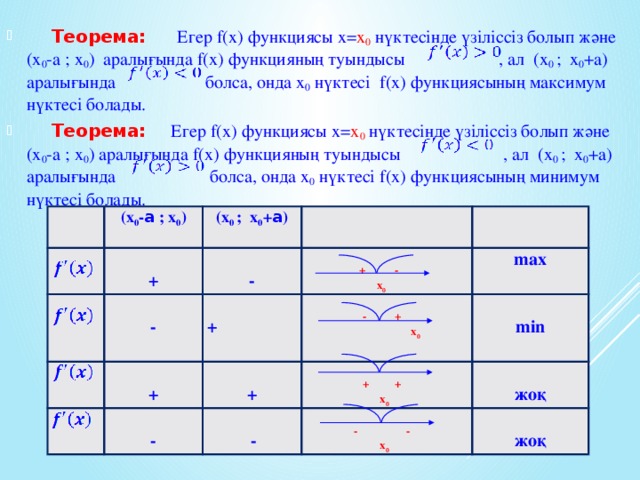
?Сынды? н?ктелер. Функцияны? экстремумдері
?Саба?ты? ма?саты:
?Функцияны? сынды? н?ктесіне аны?тама беру.
?Туындыны ?олданып функцияны? экстремум н?ктелерін я?ни максимум ж?не минимум н?ктелерін аны?тауды ?йрету.
? Функцияны? сынды? н?ктесі жо? болса ж?не сынды? н?ктелер барлы? уа?ытта экстремум н?ктелері болмайтынды?ын т?сіндіру.
?