11 класс
Учитель математики
МАОУ СОШ №30, г. Челябинска
Юрченко Ольга Павловна
Цель урока:
- Обобщение знаний по теме «Тела вращения»: нахождение
основных элементов фигур, площади поверхности.
- Закрепление навыков решения задач уровня ЕГЭ.
- Развитие самостоятельности при решении задач.
- Развитие алгоритмического мышления.
- Развитие пространственного воображения.
- Воспитание контроля и самоконтроля.
Г. Галилей
момент
5 мин
2. Актуализация знаний (блиц-опрос)
5 мин
3. Сообщения учащихся
(историческая справка)
5 мин
4. Решение задач уровня ЕГЭ
15 мин
5. Самостоятельная работа
10 мин
6. Итог урока.
5 мин
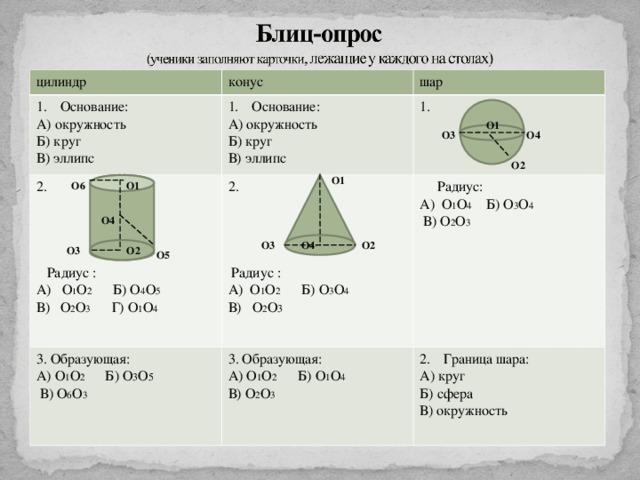
цилиндр
конус
А) окружность
Б) круг
В) эллипс
шар
2.
Радиус :
А) О 1 О 2 Б) О 4 О 5
В) О 2 О 3 Г) О 1 О 4
1.
2.
Радиус :
А) О 1 О 2 Б) О 3 О 4
В) О 2 О 3
3. Образующая:
А) О 1 О 2 Б) О 3 О 5
В) О 6 О 3
А) окружность
Б) круг
В) эллипс
3. Образующая:
А) О 1 О 2 Б) О 1 О 4
В) О 2 О 3
Радиус:
А) О 1 О 4 Б) О 3 О 4
В) О 2 О 3
А) круг
Б) сфера
В) окружность
О1
О3
О4
О2
О1
О6
О1
О4
О2
О3
О4
О3
О2
О5
цилиндр
конус
4. Высота цилиндра - это:
А) расстояние между
плоскостями его
основания Б) отрезок, который
соединяет две любые
точки оснований В) отрезок, который
соединяет центр круга
с любой точкой
цилиндра
шар
4. Высота конуса – это:
А) отрезок, соединяющий вершину с любой точкой основания
Б) расстояние от вершины конуса до основания
В) отрезок, соединяющий вершину с точкой, лежащей на окружности
3. Сечение шара:
А) окружность
Б) круг
В) эллипс
площади боковой
поверхности
цилиндра
5. Напишите формулу площади боковой поверхности конуса
4. Напишите формулу поверхности шара
ндра
Шаром принято называть тело,
ограниченное сферой, т.е. шар и сфера –
это разные геометрические тела.
Однако оба слова «шар» и «сфера» происходят от одного и того же
греческого слова «сфайра» - мяч. При этом слово «шар» образовалось
от перехода согласных сф в ш .
В Х I книге «Начала» Евклид определяет шар как фигуру, описанную
вращающимся около неподвижного диаметра полукругом.
В древности сфера была в большом почёте. Астрономические
наблюдения над небесным сводом неизменно вызывали образ сферы.
Сфера всегда широко применялась в различных областях науки и техники .
Слово цилиндр происходит от греческого слова
, что означает «валик», «каток».
Конус в переводе с греческого “konos” означает
«сосновая шишка».
С конусом и цилиндром люди знакомы с глубокой древности.
Архимед решил задачу об объеме общей части
пересекающихся цилиндров.
Демокрит получил формулу для вычисления объема
пирамиды и конуса.
Школе Платона принадлежит:
а) исследование свойств цилиндра и конуса;
б) изучение конических сечений.
Большой трактат о конических сечениях был написан
Аполлонием Пергским – учеником Евклида
В геологии существует понятие « конус выноса ». Это форма рельефа,
образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными
горными реками на предгорную равнину или в более плоскую широкую долину .
В биологии есть понятие « конус нарастания ». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
« Конусами » называется семейство морских
моллюсков. Раковина коническая (2–16 см),
ярко окрашенная.
По статистике на Земле ежегодно гибнет от разрядов
молний 6 человек на 1000 000 жителей .
Этого бы не случалось, если бы везде были громоотводы,
так как образуется конус безопасности. Чем выше
громоотвод, тем больше объем такого конуса.
Высота конуса равна 10, а диаметр основания – 48.
Найдите образующую конуса.
10
?
48
Ответ: 26
Высота конуса равна 6, а длина образующей – 10.
Найдите диаметр основания конуса
6
10
?
Ответ: 16
Площадь боковой поверхности цилиндра равна 16π, а диаметр основания – 8. Найдите высоту цилиндра.
8
Решение:
S = 2 π R h
→ 16 π = 8 π h
h = 2
2R =8
S = 16 π
Ответ: 2
Найдите радиус сферы, если площадь сферы равна 16π
Решение:
S = 4 π R²
16 π =
4 π R²
→
R = 2
S = 16 π
Ответ: 2
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Решение:
S = π RL
3L
S 1 = π R(3L) = 3 ( π RL ) = 3 S
L
R
R
Ответ: в 3 раза
π R² =3 4 π R²=12 Ответ: S шара = 12" width="640"
4
Задачи из банка данных ЕГЭ (устное решение задачи)
Около шара описан цилиндр, площадь
поверхности которого равна 18.
Найдите площадь поверхности шара.
Решение:
6 π² = 18
=
π R² =3
4 π R²=12
Ответ: S шара = 12
Прямоугольный параллелепипед
описан около единичной сферы.
Найдите его площадь поверхности .
Решение:
Т.к. сфера вписана в параллелепипед, то ABCDA 1 B 1 C 1 D 1 является кубом, в котором а = 2 R = 2 ∙ 1 = 2
Значит, S = 6a² = 6 ∙ 2²= 24
Ответ: 24
ВО = ∙ 4 = 2, Значит, S = 8 πR = 8π ∙ 2 = 16π Ответ: 16π" width="640"
Равнобедренный треугольник, у которого боковые стороны
равны по 4см, а один из углов 120 ° , вращается вокруг прямой,
содержащей большую сторону.
Найдите площадь поверхности полученного тела.
B
4
4
120 ̊
A
C
O
Решение:
= 2 πR ∙ 4 = 8 πR
S = 2 S бок. = 2 π RL
т.е. R = 2
АВ=
Из ∆ АВО: ∟А = 30˚ = ВО =
∙ 4 = 2,
Значит, S = 8 πR = 8π ∙ 2 = 16π
Ответ: 16π
Прямоугольник с периметром 16см и площадью 15см 2 вращается
вокруг большей стороны. Найдите площадь поверхности тела вращения .
B
C
Решение:
S = S бок. + 2 S осн.
S = 2πRh + 2πR 2
Из прямоугольника ABCD : S = AB ∙ BC = 15
P = 2 ( AB + BC ) = 16
Или, Rh = 15
R + h = 8,
Ответ: 48π см 2
D
A
значит, R = 3, h = 5
Таким образом,
S = 2 π ∙15 + 2 π ∙ 3 2 =
48π (см 2 )
1 вариант
2 вариант
1. Образующая конуса
5 см, высота 4 см. Найдите площадь боковой поверхности конуса.
1. Высота конуса 4 см, а радиус основания 3см. Найдите площадь поверхности конуса.
2. Осевым сечением цилиндра является квадрат, площадь которого 100см². Найдите площадь боковой поверхности цилиндра.
2. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 20см. Найдите радиус основания цилиндра.
Ответы: 1 вариант – 15 π ; 100 π
2 вариант – 24 π ; 5√2
Итог урока
1. Домашнее задание
Поставьте вопросы к данным условиям задач и решите их:
- Дан шар, радиус которого 2см.
- Длина окружности основания цилиндра 8 π см, а диагональ
осевого сечения 17см.
- Прямоугольная трапеция с основаниями 2 и 5 см и меньшей боковой стороной 4 см вращается вокруг большего основания.
2. Рефлексия ( бланки опроса лежат на столах учащихся ).
Поставьте «плюс» или «минус» напротив каждого утверждения
- Я знаю формулы для нахождения площадей поверхностей тел вращения.
- Я понял, как решать типовые задачи уровня ЕГЭ.
- Я расширил свои знания о телах вращения.
