Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Урок алгебры в 8 классе "Теорема Виета"
Урок нового материала. Используються элементы оформления заданий по ОГЭ. В презентации отражены все этапы урока с выходом на ЦОР для решения задач новой теоремы и обратной. Элементы исследования актуализировали обучающихся на изучение нового. Домашнее задание связано с решением квадратных уравнений и называется творческим с помощью дешифратора по методу таблицы умножения – находите буквы и вписываете их в последний столбец.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Открытый урок в 8 классе»
Просмотр содержимого документа
«таблица мои цели урока»
Просмотр содержимого презентации
«мой урок теорема Виета »
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
1680 руб.
2400 руб.
1390 руб.
1980 руб.
1360 руб.
1940 руб.
Курсы ПК и ППК для учителей!
500 руб.
2500 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

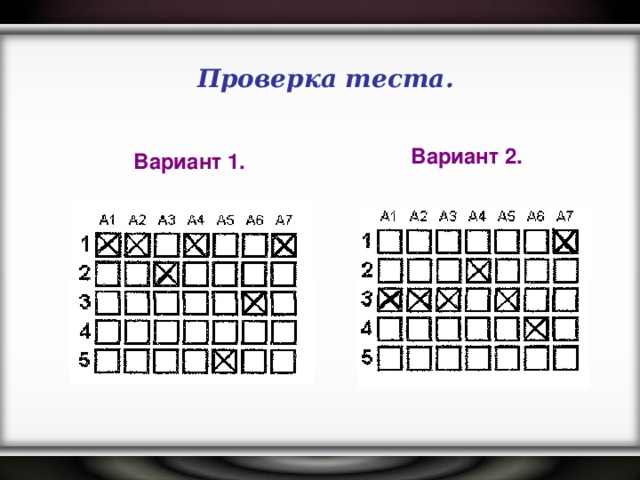
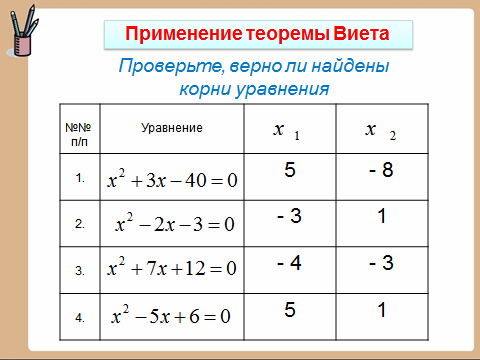
 СЛАЙД № 2
СЛАЙД № 2 СЛАЙД 3, я начинаю, а вы заканчиваете фразу. Готовы??? Тогда начали.
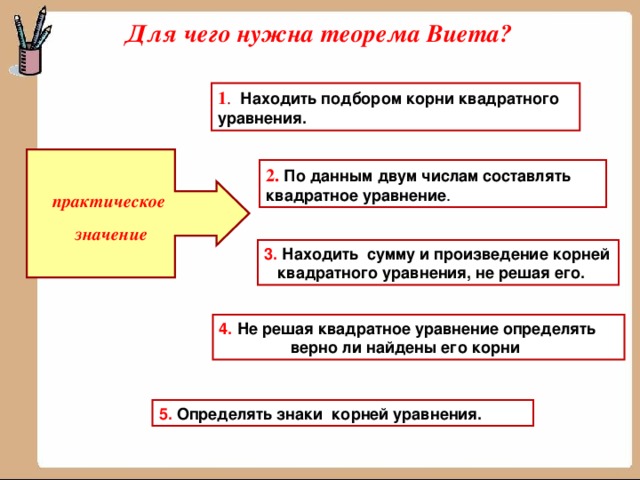
СЛАЙД 3, я начинаю, а вы заканчиваете фразу. Готовы??? Тогда начали.
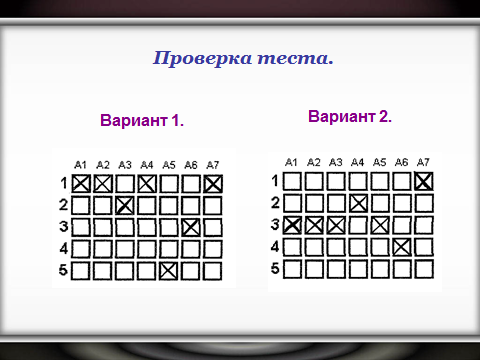
 (Проверка осуществляется по щелчку)
(Проверка осуществляется по щелчку)
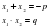
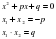 ( записать в тетрадях и на доске)
( записать в тетрадях и на доске)



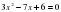 1)
1) 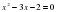
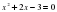 6)
6) 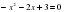
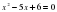 равна
равна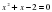 равно
равно











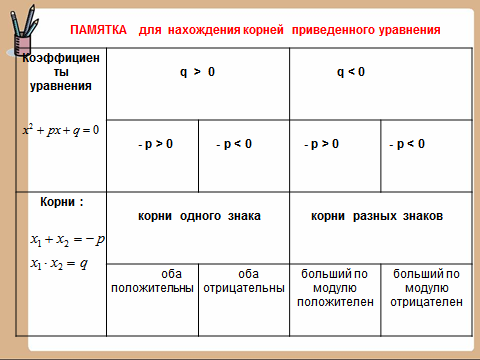
 0 - p 0 Корни : q - p корни одного знака оба положительны - p 0 корни разных знаков оба отрицательны - p больший по модулю положителен больший по модулю отрицателен" width="640"
0 - p 0 Корни : q - p корни одного знака оба положительны - p 0 корни разных знаков оба отрицательны - p больший по модулю положителен больший по модулю отрицателен" width="640"