6
Муниципальное образовательное учреждение
Средняя общеобразовательная школа №68
Учебно-исследовательская
работа
«Будем умными вдвойне, посчитаем все в уме»
секция математики
Выполнили: Порсина Ирина
ученица 8 «В» класса
Шевченко Маргарита
ученица 7 «Б» класса
Руководитель: Потеряйкина Ольга Николаевна
учитель математики
г. Хабаровск
2013 г.
Содержание
Введение……………………………………………………………………..3
Устный счет………………………………………………………………5
Если углубиться в историю ……………………………………………6
Феномен особых способностей в устном счёте……………………….8
Таблица умножения на пальцах………………………………………...9
3.1 Умножение на 9…………………………………………………...9
3.2 Умножение на 8…………………………………………………...9
3.3 Умножения на пальцах после пяти…………………………….10
Приемы быстрого счета…………………………………………………11
4.1 Умножение на 11…………………………………………………11
4.2 Возведение в квадрат чисел, оканчивающихся на 5 ………….11
4.3 Умножение двузначных чисел, близких к 10………………….12
4.4 Умножение двузначных чисел, близких к 100………………...12
4.5 Извлечение квадратных корней…………………………………13
Исследовательская работа………………………………………………14
Заключение…………………………………………………………………..15
Список литературы………………………………………………………….16
Приложение 1………………………………………………………………..17
Приложение 2………………………………………………………………..19
.
Введение
Интерес к данной теме возник в связи с регулярным проведением математических диктантов в классе на уроках математики. Наша учительница убедила нас в необходимости научиться считать быстро и правильно, но как этого добиться. На уроках она показала нам несколько приемов, позволяющих облегчить выполнение арифметических действий. Мы решили проверить на практике: действительно ли можно помочь классу считать быстро. Для начала решили найти в литературе и другие приемы быстрого счета, овладеть ими самим и показать эти приемы одноклассникам. Наша учитель математики поддержала нас в этом начинании и сказала, что даст возможность на уроке проверить эффективность приемов счета и проверить нашу гипотезу.
В настоящее время учащиеся пользуются калькуляторами и компьютерами. Кажется, отпала необходимость в отработке устного счета. Но это ошибочное мнение. Устный счет на уроках математики на современном этапе особенно актуален, так как повышает скорость вычислительной работы, что ценно, а главное - развивает мышление.
Вычислительные навыки необходимы как в практической жизни каждого человека, так и в учении. Ни один пример, ни одну задачу по математике, физике, химии и т. д. нельзя решать, не обладая элементарными способами вычислений.
Серьёзный шаг в жизни каждого выпускника – Единый государственный экзамен (ЕГЭ), развитые вычислительные умения и наличие навыков устного счета - залог успешной его сдачи.
Цель нашей работы заключалась в следующем: изучение методов и приемов быстрого счета и доказательство необходимости умения быстрого счета и эффективного использования этих приемов. А главное, определение значимости навыков устного счета для успешной сдачи учащимися 11 классов Единого Государственного Экзамена.
Мы поставили перед собой следующие задачи:
Воспользовавшись различными источниками информации собрать, изучить и систематизировать материал о приемах устного счета.
Рассмотреть некоторые приемы устного счета и на конкретных примерах показать преимущества их использования.
Для младших школьников провести мастер-класс
Для старшеклассников провести микро исследование : «Наличие навыков устного счета залог успешной сдачи экзамена»
Методами нашего исследования были:
анкетирование
демонстрация презентации
анализ полученных данных
У́стный счёт
Мы посмотрели в словаре, что же такое – устный счет?
У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств ( компьютер, калькулятор, счеты и т. п.) и часто без приспособлений ( ручка, карандаш, бумага и т. п.).
Если углубиться в историю, можно заметить,что и в прошлые века устный счет был одним из главных компонентов урока. В XIX веке художник Н.П.Богданов- Бельский написал картину «Усный счет»(1895г.). На ней изображен фрагент урока математики в школе села Татево Смоленской губернии, которую основал и в которой работал С.А.Рачинский – учитель художника, автор ряда книг по занимаельной математике: «1001 задача для устного счета», (рис.1) «Арифметические забавы», «Геометрические забавы».

(рис.1)
Если углубиться в историю
Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникало необходимость отвечать на жизненно важные вопросы: поскольку плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас; сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.
Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.
Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета. .
При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.
Особенно сложны и трудны были в старину действия умножения и деления -- особенно последнее. «Умноженье -- мое мученье, а с делением -- беда», -- говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления - приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». Наш современный способ умножения описан там под названием «шахматного». Был также и очень интересный, точный, легкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. На протяжении своей книги в 640 страниц Леонтий Магницкий («Арифметика» - старинный русский учебник математики, которую Ломоносов называл «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.
Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.
Феномен особых способностей в устном счёте
Феномен особых способностей в устном счёте встречается с давних пор. Как известно, ими обладали многие учёные, в частности, Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.
До второй половины XX века на эстраде были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой. Известными российскими «суперсчетчиками» являются Арон Чиквашвили, Давид Гольдштейн, Юрий Горный, зарубежными: Борислав Гаджански, Вильям Клайн, Томас Фулер и другие.
Хотя некоторые специалисты уверяли, что дело во врождённых способностях, другие аргументированно доказывали обратное: «дело не только и не столько в каких-то исключительных, „феноменальных“ способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.
Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счета создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием "Системы быстрого счета". История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.
Таблица умножения на «пальцах».
Таблица умножения - те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах дается совсем не элементарно. Это потом уже с легкостью мага мы "щелкаем" примеры на умножение: 2·3, 3·5, 4·6 и так далее. С возрастом, правда, все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой "ручного" умножения, мы можем запросто отказаться от услуг калькулятора. Но сразу уточним, что говорим только о школьной таблице умножения, то есть для чисел от 2 до 9, умножаемых на числа от 1 до 10.
Умножение для числа 9 - 9·1, 9·2 ... 9·10 - легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится "на пальцах". Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки .
Допустим, хотим умножить 9 на 8. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 8. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа - количество единиц. Слева у нас 7 пальцев не загнуто, справа - 2 пальца. Таким образом, 9·8=72. Вместо пальцев можно использовать клетки.(рис.2)
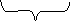

7 клеток (рис.2) 2 клетки
Умножение для числа 8 - 8·1, 8·2 ... 8·10 - действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца - с номером x и следующий палец с номером x+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось незагнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять "на пальцах", чем ниже число расположено от 9.
Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 4. Загибаем палец с номером 4 и за ним палец с номером 5 (4+1). Слева у нас осталось 3 незагнутых пальца, значит нам необходимо загнуть еще 3 пальца после пальца с номером 5 (это будут пальцы с номерами 6, 7 и 8). Осталось 3 пальца не загнуто слева и 2 пальца - справа. Следовательно, 8·4=32. 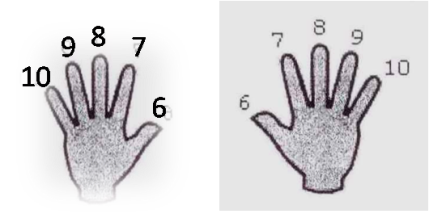
Но, оказывается, есть ещё способ умножения на пальцах второй части таблицы умножения. До пяти все знают наизусть таблицу умножения, а после пять с затруднениями после пяти так же можно умножать (рис.3)
на пальцах.
Задача1 Умножить 8∙7. Надо положить руки перед собой, на левой руке от большого пальца начинаем отсчитывать от 6 до 10 и так же на правой руке (рис.3) И для этого надо загнуть на левой руке все пальцы до 7, а на правой руке все пальцы до 8. Начинаем считать те пальцы, которые остались не загнутыми, мы их прибавляем между собой, а загнутые пальцы перемножаем между собой. И так получается 56.
Задача2 Умножить 6∙6. Кладем руки перед собой, на левой руке от большого пальца начинаем отсчитывать от 6 до 10 и так же на правой руке. А теперь считаем. На левой руке загибаем пальцы до 6,и так же на правой. Те которые пальцы не загнутые мы их перемножаем -это у нас единицы, а те которые загнутые прибавляем – это сотни. Потом сотни прибавляем к единицам. И у нас получается ответ-36.
Приемы быстрого счета
Умножение на 11
Пусть, например, нужно умножить 26 на 11. Достаточно сложить цифры 2 + 6 =8 и поставить эту восьмерку между 2 и 6, чтобы сразу сказать ответ. При сложении может получиться и двузначное число, начинающееся с 1, тогда эту единицу нужно прибавить к цифре десятков, а в середину вставлять только цифру единиц суммы. Например, при умножении 75 на 11 складываем 7 и 5, получим 12, 1 прибавляем к 7, а 2 вставляем между 8 и 5. Получаем ответ 825.
Следующее равенство объясняет, на чем основан этот способ умножения:
(10а+в)∙11=110а+11в=100а+10(а+в)+в.
Возведение в квадрат чисел, оканчивающихся на 5
Есть замечательный способ возведения в квадрат двузначных чисел, оканчивающихся цифрой 5. Для возведения такого числа в квадрат надо умножить цифру десятков на следующую за ней цифру, а 5 возвести в квадрат и приписать результат – 25 после полученного произведения.
Например, 35²=1225 (так как 3∙4=12); 85²=7225 (так как 8∙9=72).
Есть еще один интересный способ возведения в квадрат двухзначных чисел, начинающихся с 5-ти.
Чтобы возвести в квадрат число, начинающееся на 5, надо:
к 52=25 прибавить число единиц «а».
К полученному числу приписать справа квадрат единиц.
562=(25+6)∙(62)=3136
592=(25+9)∙(92)=348
Возведение в квадрат двухзначных и трёхзначных чисел.
ПРАВИЛО:
умножают число десятков на число, на единицу больше, и к произведению приписывают 25.
752=(7∙8) в конец произведения подписываем 25 =5625
Умножение двузначных чисел, близких к 10
Применяется прием умножения в столбик, только устно. Сначала умножают единицы (это и будет значение единиц в ответе), затем умножают десятки (это будет значение сотен в ответе). Чтобы получить десятки нужно перемножить единицы одного числа на десятки другого и полученные произведения сложить.
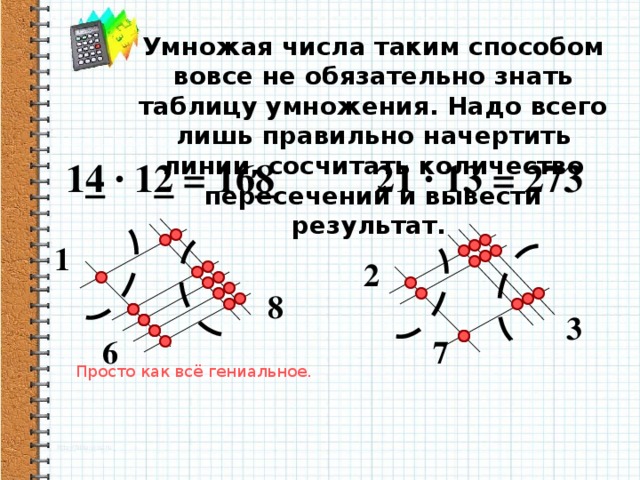
Есть очень интересный графический способ умножения дузначных чисел По некоторым сведениям, так умножают числа в Китае и Японии. Перемножается каждая цифра на каждую. Результаты складываюся с определением позиции (сдвигом) и с переносом старшего разряда. Сдвиг - это сумма позиций перемножаемых цифр, считая справа налево. Суть предлагаемого метода - определение сдвига графически, с помощью наклоненного прямоугольника. Произведение самых младших цифр получает нулевой сдвиг, произведения последних цифр на предпоследние - таких произведений два - сдвигаются на один разряд при суммировании и так далее.
Метод верный, но больше подходит для эрудиции. На практике считать привычным столбиком всё равно удобнее.
Умножение двузначных чисел, близких к 100
Всякое двузначное число можно представить в виде 100—а. Будем называть а недостатком данного числа до 100. Если данные числа близки к 100, то недостатки их — сравнительно небольшие числа, удобные для устных вычислений. Рассмотрим такое умножение в общем виде: (100 – а) (100 – b) = 100×100 – 100а – 100b +аb = (100 –а – b)100+аb. Это выражение показывает: чтобы получить число сотен искомого произведения, достаточно из одного сомножителя (например, 100—а) вычесть недостаток другого сомножителя (т. е. b) и к полученной разности приписать произведение недостатков аb, если аb — число двузначное. Если аb — однозначное число, например 8, то приписывается 08.
Умножить 87 на 94. Первый недостаток 13, второй 6. Из 87 вычитаем 6 (или из 94 вычитаем 13), получаем 81. К 81 приписываем 13-6 = 78. Произведение 8178. Идею этого интересного способа легко распространить и на умножение двух трехзначных чисел, близких к 1000. Умножим, например, 985 на 992. Первый недостаток 15, второй 8. Вычитая 8 из 985 (или 15 из 992), получим 977 — число тысяч искомого произведения. Приписав к 977 произведение недостатков 15-8 = 120, получим произведение 977 120
Извлечение квадратных корней
Учащимся очень часто приходится извлекать арифметический квадратный корень из числа без помощи калькулятора. Здесь помощниками являются вспомогательные таблицы – таблица квадратов «круглых» чисел а и таблиц цифр, являющихся окончанием квадратов чисел от 0 до 9
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 | 10 | 100 |
|
| 20 | 400 |
| 30 | 900 |
| 40 | 1600 |
| 50 | 2500 |
| 60 | 3600 |
| 70 | 4900 |
| 80 | 6400 |
| 90 | 8100 |
| 100 | 10000 |
таблице№2
Например:
√576 = 24
√3204 = 48
√3939 = 63
√8836 = 94
Число десятков определяют по таблице№1, число единиц находят по таблице№2
таблице№1
Исследовательская работа
Мы провели анкетирование учащихся
Любите ли вы устный счёт?
Быстро ли вы считаете устно?
Сможете ли решить устно пять примеров за 2 минуты?
Знали ли вы эти приёмы?
Понадобится ли в дальнейшем вам эта информация?
Знаете ли вы другие способы лёгкого устного счёта
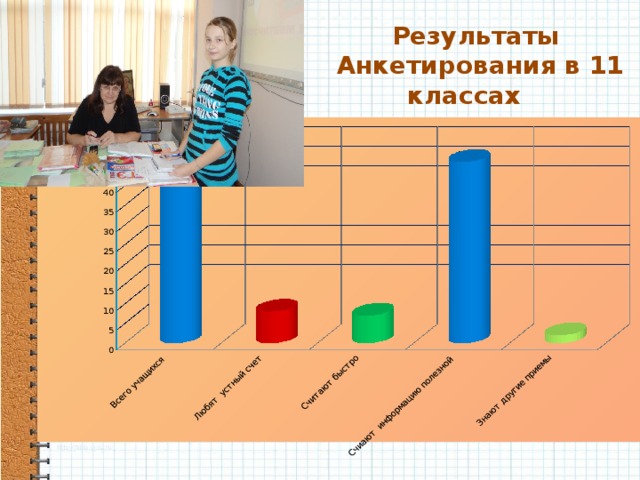
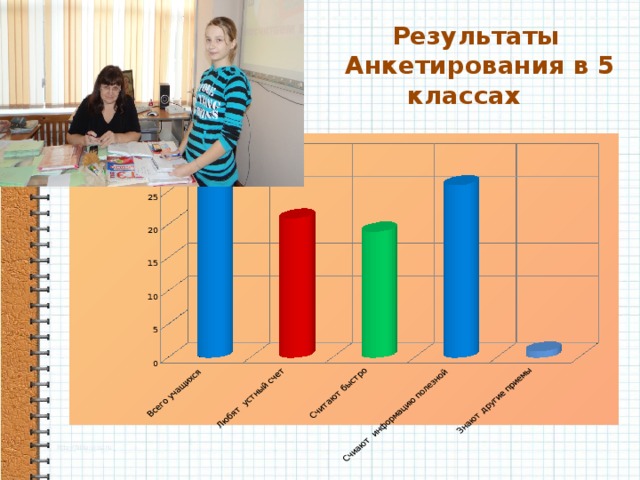
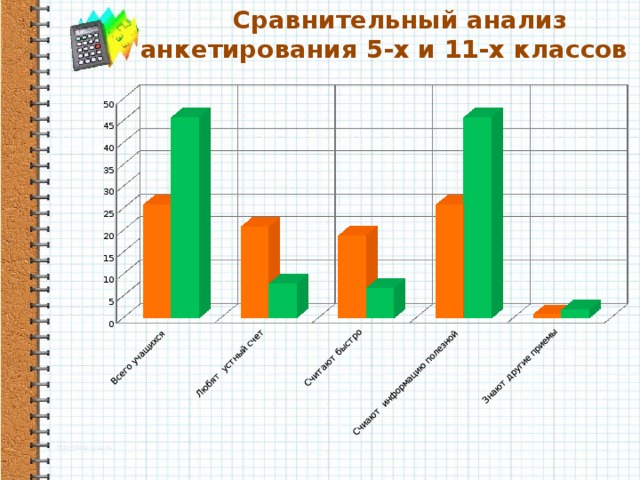
По результатам анкетирования видно, что пятиклассники и любят устный счет и быстрее считают. Сиаршеклассники же предпочитают калькулятор, что недопустимо на ЕГЭ. Все учащиеся считают информацию полезной! К сожалению, мало ребят знают приемы устного счета. (приложение1)
Для исследования мы выбрали самые необходимые, на наш взгляд приемы устного счета
Умножение двузначных и трехзначных чисел на 11
Возведение в квадрат чисел, оканчивающихся на 5
Умножение двузначных чисел, близких к 100
Умножение двузначных чисел, близких к 10
Извлечение арифметического квадратного корня
234 ∙ 11
652
97 ∙ 81
43 ∙ 13
√2304
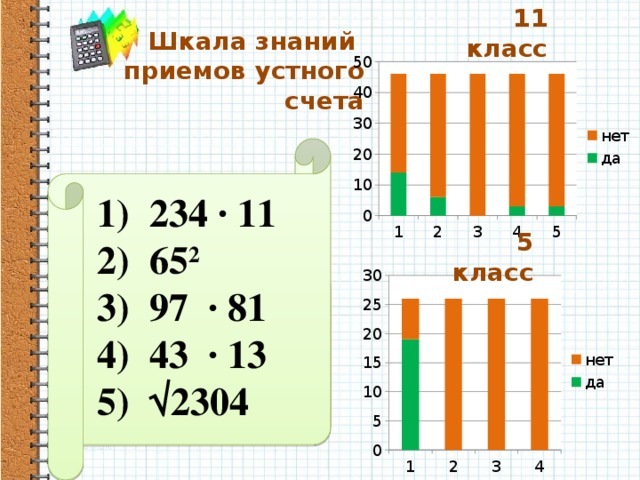
Как выяснилось, из предложенных приемов, учащиеся 5 и 11 классов, знали совсем немногие. На диаграмме (Приложение 2) выдно, что среди 11 классников только одна треть учащихся знакома с первым приемом устного счета, единицы знают о втором, четвертом и пятом приемах устного счеа, и никто их учащихся не знал прием умножения двузначных чисел, близких к 100
Заключение
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности.
Повышение познавательного интереса, это длительный процесс поэтому в ходе нашей экспериментальной работы не у всех учащихся повысился уровень познавательного интереса. Мы считаем что причиной этого является недостаточность количества времени. Но в целом наша экспериментальная работа прошла плодотворно и мы можем только предложить учителю продолжать использовать на уроках устные упражнения для повышения уровня познавательного интереса.
Математика - предмет настолько серьезный, что воспользоваться каждой возможностью оживления уроков – чрезвычайно важно.
Из результата экспериментальной работы можно сделать вывод, что уровень познавательного интереса детей значительно повысился и это свидетельствует о том, что предложенные нами виды устных упражнений оказались эффективными .
Используя различные приемы устного счета, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
Такие навыки помогут школьникам в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет - настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения.
Наша гипотеза подтвердилась – наличие навыков устного счета – залог успешной сдачи экзамена.
Список литературы
Вроблевский. Как научится легко и быстро считать. -- М.-1932.-132с.
Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/
Перельман А.И. Быстрый счет. Тридцать простых приемов устного счета, Ленинград, 1941г.
Сорокин А. С. Техника счета. М., "Знание", 1976.
Приложение 1
Результаты анкетирования в 11 классах
![]()
Результаты анкетирования в 5 классах
![]()
Сравнительный анализ анкетирования 5-х и 11-х классов
![]()
Приложение 2
Знание приемов устного счете
11 класс
![]()
5 класс
![]()