Тема: Взаимное расположение графиков функций
Цель: познакомить учащихся со взаимным расположением графиков функций на координатной плоскости; научить решать задания по данной теме.
Развивать: навык построения графиков; логическое мышление;
Воспитать: познавательную активность;
Тип урока: комбинированный
Просмотр содержимого документа
«Взаимное расположение графиков функций »

Ученье свет, а не ученье-
тьма

-71
19-90=
121-145=
65-80=
-78-72=
-56-89=
35+35-70=
145-175=
-24
-15
-150
-145
0
-30

300
-200+500=
198-300=
23-45=
100:(-20)=
-9:(-3)=
4,2:(-6)=
9*(-5)=
-120*(-5)=
-102
-22
-5
3
-0,7
-45
600

Взаимное расположение графиков линейных функций .

1. Пересечение графиков двух линейных функций, построенных на одной координатной плоскости.

Пример 1.
Найти точку пересечения графиков функций:
у=2х+1 и у=0,5х+4
2х+1=0,5+4
2х-0,5х=-1+4
1,5х=3
х=3:1,5
х=2.

5
5
Если х=2, то у=2*2+1= и у=2*0,5+4=
Значит точка пересечения графиков данных функций будет т.А(2;5).
Обратите внимание, если k1=2 k2=0,5, то
k1≠ k2.
Задание:
Постройте графики функций у=2х+1 и у=0.5х+4 и проверьте, пересекаются ли они в т.А(2,5)

Определение.
Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются.
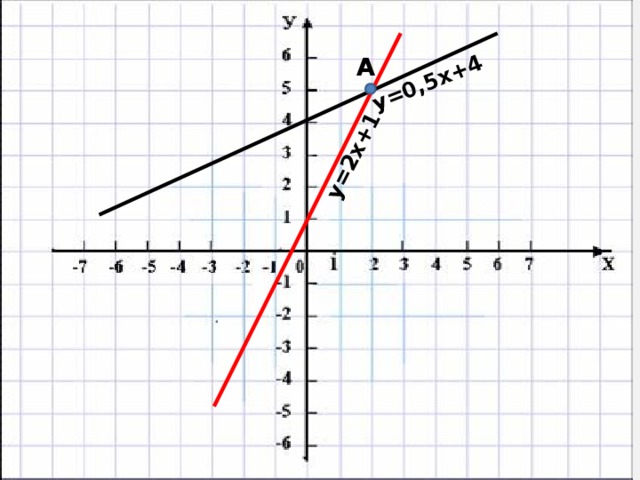
у=2х+1
у=0,5х+4
А

2. Параллельность графиков двух линейных функций, построенных в одной координатной плоскости.

Пример 2 .
Даны функции у=1,5х+2 и у=1,5х-2.
1,5х+2=1,5х-2
1,5х-1,5х=-2-2
0*х=-4
Уравнение не имеет корней.
Обратите внимание: k1=1,5 и k2=1,5, следовательно k1=k2

Определение.
Если угловые коэффициенты прямых, являющихся графиками линейных функций равны, то прямые параллельны.
Проверить, действительно ли графики функций у=1,5х+2 и у=1,5х-2 – параллельны.
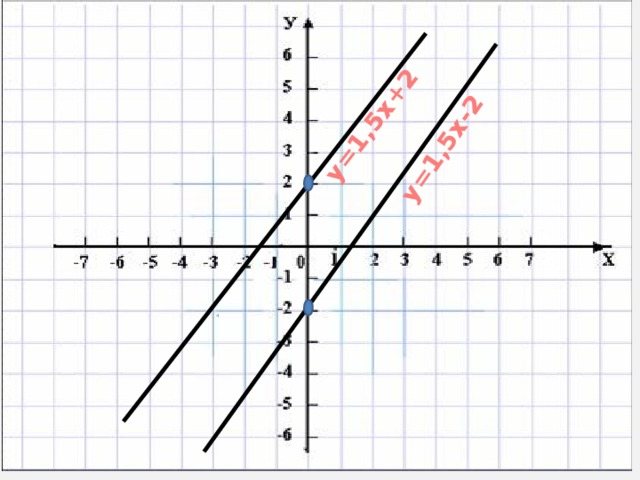
у=1,5х+2
у=1,5х-2

Решение по учебнику:
№ 1388 (устно)
№ 1390(1-3), 1391(1-3), 1392, 1395
Домашнее задание:
§ 7.6 – прочитать, ответить на вопросы в конце параграфа.
№ 1390 (4), 1391 (4)


































