Цель: Демонстрация педагогического мастерства в передаче инновационного опыта, перспектива использования данного ресурса в системе повышения квалификации учителей.
Пояснительная записка.
Психологические аспекты в обучении математике.
Педагогическая теория - абстракция. Ее практическое применение - всегда высокое искусство.
Всякая программа преподавания, всякая методика воспитания, как бы хороши они ни были, без личности учителя остаются мертвой буквой, не имеющей никакой силы в действительности. "Посредственный учитель излагает, хороший учитель объясняет, выдающийся учитель показывает, великий учитель вдохновляет», - писал английский философ Уильям Уорд. «Все математические объекты и понятия являются абстрактными и лишенными вещественных основ. Поэтому все, что только можно, предоставляется для восприятия чувствами, а именно: видимое - для восприятия зрением, слышимое – слухом, запахи – обонянием, подлежащее вкусу – вкусом, доступное осязанию – путем осязания. Если какие-либо предметы сразу можно воспринять несколькими чувствами, пусть они сразу схватываются несколькими». ( Я. А. Коменский). На прочность усвоения учебного материала большое влияние оказывают мотивы учащихся, их интерес к изучаемой теме, положительные эмоции, возникающие при усвоении материала. Закономерность Смирнова – Зинченко гласит: « Учащийся может запомнить материал непроизвольно, если выполняет над ним активную мыслительную деятельность, и она направлена на понимание этого материала». В то же время восприятие математических объектов облегчается, если оно не требует больших усилий со стороны наших органов чувств. Развитие воображения наряду с мышлением является весьма важной задачей обучения математике. Без развитого воображения невозможно полноценное усвоение математики, особенно геометрии. Воображение – психический процесс создания новых умственных образов, на основе переработки образов восприятия, хранящихся в нашей памяти. Создание образов позволяет с максимальной возможной вероятностью разрешить возникшие трудности. Воображение дает возможность создать яркий наглядный образ события, явления, понятия, процесса. Задача педагога не только дать ученику информацию, но и помочь переработать ее в собственные знания. Не подменяя научную специальную терминологию для облегчения восприятия и запоминания математических понятий, терминов и фактов можно использовать следующие приемы.
Не каждому ученику по силам осознанно и правильно объяснить, что в том или ином случае он использовал закон умножения относительно сложения, а «правило фонтанчика» знают почти все:

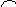
a ( b + c ) = a b + a c ,
где стрелки показывают, как необходимо правильно выполнить умножение числа на сумму.« Правило фонтанчика» помогает учащимся усвоить и без ошибок применять на практике не только распределительное свойство умножения относительно сложения и вычитания (5 класс), но и правило раскрытия скобок ( 6 класс ), а так же правило умножения одночлена на многочлен ( 7 класс ).
Можно переформулировать задачи на язык жестов, мимики, ассоциаций на этапе введения, что в конечном итоге положительно повлияет на усвоение. В 6 классе при изучении темы «Решение уравнений», для того чтобы учащиеся лучше усвоили правило переноса слагаемых из одной части уравнения в другую, предлагаю учащимся представить уравнение как две страны (левая часть и правая часть), разделенные границей (знак равенства). Можно представить жителей разных стран, которые при переходе через границу меняют свои паспорта (слагаемые при переносе из одной части уравнения в другую должны изменить свой знак на противоположный).
2 х – 1 = 11 – х
2 х + х = 11 + 1
Ученики легче воспринимают правило и быстро запоминают.
Разбирая понятие неправильной дроби можно обратить внимание на тяжесть. Где удобнее носить тяжелые вещи вверху ( поднимаем руки над головой ) или внизу? Ответ очевиден. Что делать с неправильной дробью у которой тяжесть вверху?
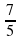 = 1
= 1 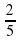
Где теперь тяжесть? Внизу, правильно.
Избавляясь от иррациональности, представим ее в виде шляпы. А где носят шляпу? Ответ очевиден.
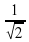 =
= 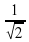 *
* 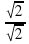 =
= 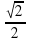
Теперь шляпа на месте.
Восьмиклассники часто ошибаются при изображении на координатной прямой числовых промежутков, являющихся решением неравенств с одной переменной. Но, если попросить учащихся представить знаки 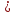 и
и 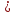 как стрелки → ,←, то они без труда показывают на числовой прямой решение неравенств вида х
как стрелки → ,←, то они без труда показывают на числовой прямой решение неравенств вида х 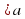 или х
или х 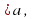 заштриховывая ту часть прямой на которую указывает стрелка . х -
заштриховывая ту часть прямой на которую указывает стрелка . х - 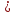 3.
3.
Путаются учащиеся и с формулой перехода логарифма к новому основанию. Несколько наводящих вопросов помогут решить проблему.
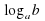 =
= 
Простой прием запоминаний формул приведения
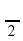
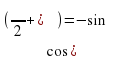

 1. Где на единичной окружности лежит точка
1. Где на единичной окружности лежит точка 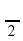 , на
, на
 вертикали, или на горизонтали. Спрашиваем : « Меняем
вертикали, или на горизонтали. Спрашиваем : « Меняем
 на
на 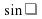 или не меняем ? Ответ получим кивая
или не меняем ? Ответ получим кивая
головой, проводя ею сверху вниз по оси, на которой
располагается 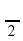 ( или кивая слева направо по оси на которой располагается
( или кивая слева направо по оси на которой располагается  ).
).
2. Определяем знак по четверти.
Различная форма записи одного и того же числа на языке ассоциаций может быть представлена приблизительно так:
-Я, Шнейдер Светлана Николаевна, зимой надеваю пальто и шапку, а весной легкий плащ, летом я надену сарафан. Перестала ли я быть Светланой Николаевной, когда переоделась?
- Нет.
-Почему я переодеваюсь?
-Так удобнее.
-Таким же свойством обладают и числа. Они «переодеваются» по необходимости. Например,
1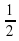 =
= 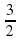 = 1,5 =
= 1,5 = 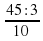 ,
,
3,5 - 1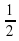 , как в данной ситуации удобнее выглядеть числу 1
, как в данной ситуации удобнее выглядеть числу 1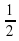 ?
?
Одно из самых коротких правил перевода десятичной дроби в обыкновенную : как слышится – так и пишется.
1,3=1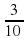
У многих ребят существует психологический барьер, связанный с необходимостью доказывать теоремы. Зачем нужно доказывать очевидные, с их точки зрения, вещи? Особенно на начальном этапе изучения геометрии. Можно в качестве домашнего задания предложить задачу.
Дан квадрат, его площадь равна 64 см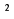 разрежьте его на части и сложите из него прямоугольник, найдите площадь полученной фигуры. Изменится ли она? Проверим. Площадь оказалась равной 65 см². Как же так? Долгие поиски истины приведут нас к итогу: « Не верь глазам своим». Нельзя пользоваться не проверенными фактами. Нужны надежные утверждения, которыми в геометрии являются теоремы.
разрежьте его на части и сложите из него прямоугольник, найдите площадь полученной фигуры. Изменится ли она? Проверим. Площадь оказалась равной 65 см². Как же так? Долгие поиски истины приведут нас к итогу: « Не верь глазам своим». Нельзя пользоваться не проверенными фактами. Нужны надежные утверждения, которыми в геометрии являются теоремы.

![]()
 8
8
![]()


 8 5 8
8 5 8
Ассоциативный метод запоминания математических предложений, понятий, терминов еще раз подтверждают слова Ушинского: «Наглядное обучение – это такое учение, которое строится не на отличенных представлениях и словах, а на конкретных образах непосредственно воспринятых ребенком ».
Рассмотрим еще несколько приемов, способствующих запоминанию тех или иных фактов, используемых мною на уроках.
6 класс тема «Умножение и деление целых чисел» проводим ассоциации:
1.Два друга спортсмена отправились на прогулку. Им хорошо вместе?
-Да. (+5*(+7)=+12)
2.Два одноклассника сбежали с урока в кино. Им хорошо вместе?
-Да. (-5*(-7)=35)
3.Один спортсмен другой лентяй им хорошо вместе?
-Нет. ( 5*(-7)=-35)
Правила сложения и вычитания положительных и отрицательных чисел хорошо запоминаются, если провести ассоциацию с долгами и доходами.
На уроках физики при обобщающем повторении, когда ученику нужно много формул выучить, хорошо помогают разные ассоциации. (Три кота на мясо- формула для определения среднего квадрата скорости 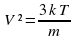 , Римма Махмудовна - вредина)- формула для определения плотности
, Римма Махмудовна - вредина)- формула для определения плотности 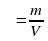 )
)
Школьники путают понятия «абсцисса» и «ордината». Ассоциация «абсцисса»- девочка, «ордината»- мальчик, мгновенно решает проблему.
Работа со слабомотивированными учениками дает большие возможности для творчества. Учитель- это тот, кто способен спуститься с высот своих знаний до незнания ученика и вместе с ним совершить восхождение. Открываю сборник по подготовке к ЕГЭ первый вариант, первая задача: «В коробке 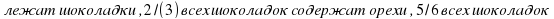 содержат изюм. Сколько процентов всех шоколадок содержат и изюм и орехи вместе?» Как объяснить такую задачу слабомотивированному ученику, чтобы он понял?
содержат изюм. Сколько процентов всех шоколадок содержат и изюм и орехи вместе?» Как объяснить такую задачу слабомотивированному ученику, чтобы он понял?
50%
В своей работе я применяю опыт учителей-новаторов:
1. Метод рационализации при решении неравенств.
2. Векторный метод при решении задач по геометрии.
3. Графический метод решения задач с параметрами.
4. Особые методы решения задач с экономическим содержанием. И многое другое.
Я бы хотела поделиться своими наработками по теме: «Решение задач на смеси и сплавы». Рассмотрим решение задач из открытого банка данных.
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Имеется два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Выясним как предложенный мною прием согласуется с требованием ФГОС. В ходе решения задач формируются универсальные учебные действия:
1. Познавательные УД (при составлении схемы для решения задачи).
2. Личностные УД (проявляется внимание).
3. Коммуникативные УД (при нахождении в тексте информации, необходимой для решения).
4. Регулятивные УД (при саморегуляции, рефлексии результатов деятельности, развитии умения выбора оптимального решения).

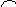
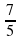 = 1
= 1 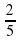
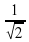 =
= 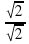 =
= 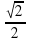
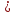 и
и 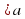 или х
или х 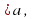 заштриховывая ту часть прямой на которую указывает стрелка . х -
заштриховывая ту часть прямой на которую указывает стрелка . х - 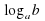 =
= 
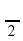
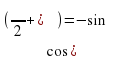

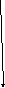 1. Где на единичной окружности лежит точка
1. Где на единичной окружности лежит точка  вертикали, или на горизонтали. Спрашиваем : « Меняем
вертикали, или на горизонтали. Спрашиваем : « Меняем  на
на 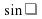 или не меняем ? Ответ получим кивая
или не меняем ? Ответ получим кивая  ).
).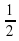 =
= 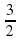 = 1,5 =
= 1,5 = 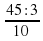 ,
,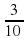
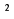 разрежьте его на части и сложите из него прямоугольник, найдите площадь полученной фигуры. Изменится ли она? Проверим. Площадь оказалась равной 65 см². Как же так? Долгие поиски истины приведут нас к итогу: « Не верь глазам своим». Нельзя пользоваться не проверенными фактами. Нужны надежные утверждения, которыми в геометрии являются теоремы.
разрежьте его на части и сложите из него прямоугольник, найдите площадь полученной фигуры. Изменится ли она? Проверим. Площадь оказалась равной 65 см². Как же так? Долгие поиски истины приведут нас к итогу: « Не верь глазам своим». Нельзя пользоваться не проверенными фактами. Нужны надежные утверждения, которыми в геометрии являются теоремы.
 8
8 

 8 5 8
8 5 8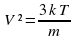 , Римма Махмудовна - вредина)- формула для определения плотности
, Римма Махмудовна - вредина)- формула для определения плотности 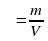 )
)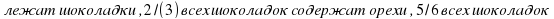 содержат изюм. Сколько процентов всех шоколадок содержат и изюм и орехи вместе?» Как объяснить такую задачу слабомотивированному ученику, чтобы он понял?
содержат изюм. Сколько процентов всех шоколадок содержат и изюм и орехи вместе?» Как объяснить такую задачу слабомотивированному ученику, чтобы он понял?