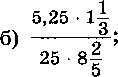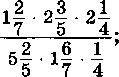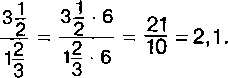Ответы на билеты по математике 6 класса
Билет №1
1. Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
Число 1 является делителем любого натурального числа.
2. Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными.
Пишут: АВ || MN. Эту запись читают: «Прямая АВ параллельна прямой MN». Если АВ || MN, то MN || АВ.
Отрезки (лучи), лежащие на параллельных прямых, называют параллельными отрезками (лучами).
3. 40
Билет №2
1. Пусть на столе лежат пачки, в каждой из которых по 8 печений. Не раскрывая ячеек, можно взять 8 печений, 16 печений, 24 печенья, а 18 печений так взять нельзя. Числа 8, 16, 24 делятся на 8, а 18 на 8 не делится. Говорят, что числа 8,3,24 кратны числу 8, а число 18 не кратно числу 8.
Кратным натурального числа а называют натуральное число, которое делится без остатка на а.
Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40. Наименьшим из кратных натурального числа является само это число.
2. Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым — номер кресла в этом ряду. При этом места (3; 8) и (8; 3) различны: первое является креслом № 8 в третьем ряду, а второе — креслом № 3 в восьмом ряду.
Подобным образом можно обозначить и положение точки на плоскости. Для этой цели на плоскости проводят две перпендикулярные координатные прямые — х и у, которые пересекаются в начале отсчета — точке 0. Эти прямые называют системой координат на плоскости, а точку 0 — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
3. 5,375
Билет №3
1. Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа.
Число 10 = 2-5. Поэтому число 10 делится без остатка и на 2, и на 5, отсюда и любое число, запись которого оканчивается цифрой 0, делится без [остатка и на 5, и на 2.
Например, 60 = 6 • 10 = 6 • (2 • 5) = (6 • 2) • 5 = 12-5, значит, 60: 5 = 12.
А из того что 60 = 6 • (5 • 2) = (6 • 5) • 2 = 30 • 2, получаем, что 60 : 2 = 30.
Каждое число можно представить в виде суммы полных десятков и единиц, например: 246 = 240 + 6, 1435 = 1430 + 5. Так как полные десятки делятся На 5, то и все число делится на 5 лишь в том случае, когда на 5 делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.
Например, числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.
Если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.
Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9.
Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
2. Пусть М — некоторая точка координатной плоскости. Проведем через нее прямую МА, перпендикулярную координатной прямой х, и прямую MB, перпендикулярную координатной прямой у. Так как точка А имеет координату 6, а точка В — координату -5, то положение точки М определяется парой чисел (6; -5). Эту пару чисел называют координатами точки М. Число 6 называют абсциссой точки М, а число -5 называют ординатой точки М. Координатную прямую х называют осью абсцисс, а координатную прямую у — осью ординат.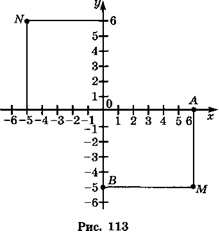
Точку М с абсциссой 6 и ординатой -5 обозначают так: М (6; -5). При этом всегда на первом месте пишут абсциссу точки, а на втором — ее ординату. Если переставить координаты местами, то получится другая точка — N (-5; 6)
3. 0,6
Билет №4
1. Число 7 делится только на 1 и само на себя. Другими словами, число 7 имеет только два делителя:1 и 7. У числа 9 три делителя: 1,3 и9. Число 11 имеет шесть делителей: 1, 2, 3, 6, 9 и 18. Такие числа, как 9 и 18, называют составными числами, а такие, как 7, - простыми числами.
Натуральное число называют простым, если оно имеет только два делите ля: единицу и само это число. Натуральное число называют составным, если оно имеет более двух делителей.
Число 1 имеет только один делитель: само это число. Поэтому его не от носят ни к составным, ни к простым числам.
2. Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Подобные слагаемые могут отличаться только коэффициентами.
Чтобы сложить (или говорят: привести) подобные слагаемые, н сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример 3. Приведем подобные слагаемые в выражении 5а + а - 2а.
Решение. В данной сумме все слагаемые подобны, так как у них одинаковая буквенная часть а. Сложим коэффициенты: 5 + 1 - 2 = 4. Значит, 5а + а - 2а = 4а.
3. 24; 20; 27
Билет №5
1. Затем выпишем все делители числа 36. Получим: 1, 2, 3, 4, 6, 9, 12, 18, 36. Общими делителями чисел 48 и 36 будут: 1, 2, 3, 4, 6, 12. Видим, что наибольшим из этих чисел является 12. Его называют наибольшим общим делителем чисел 48 и 36.
Значит, можно составить 12 подарков. В каждом подарке будет 4 конфеты «Ласточка» (48 :12 = 4) и 3 конфеты «Чебурашка» (36: 12 = 3).
Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем этих чисел.
Найдем наибольший общий делитель чисел 24 и 35.
Делителями 24 будут 1, 2, 3, 4, 6, 8,12, 24, а делителями 35 будут 1,5,7, 35. Видим, что числа 24 и 35 имеют только один общий делитель — число 1. [Такие числа называют взаимно простыми. Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
2. Число 210 является произведением чисел 21 и 10. Значит, 210 = 21 • 10. Числа 21 и 10 составные. Их тоже можно представить в виде произведений:
210= 3 • 7•10 . Получаем: 210 = 3•7•2•5. Теперь в произведении 3 • 7 • 2 • 5 все множители — простые числа. Таким образом, число 210 разложено на простые множители:
Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
При разложении чисел на простые множители используют признаки делимости.
| 756 | 2 |
| 378 | 2 |
| 189 | 3 |
| 63 | 3 |
| 21 | 3 |
| 7 | 7 |
3. 200 га
Билет №6
1. Наименьшим общим кратным натуральных чисел а и b называют наименьшее натуральное число, которое кратно и а, и b.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75 = 3 • 5 • 5, а 60 = 2 • 2 • 3 • 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа.
Получаем пять множителей 2 • 2 • 3 • 5 • 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трех и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) выписать множители, входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
2. Чтобы сравнить дроби с разными знаменателями, надо: 1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить полученные дроби.
3. 7,54
Билет №7
1. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Это свойство называют основным свойством дроби.
2. Чтобы сложить смешанные числа, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; 2) отдельно выполнить сложение целых частей и отдельно — дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
Чтобы выполнить вычитание смешанных чисел, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, то превратить ее в неправильную дробь, уменьшив на единицу целую часть; 2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
3.15
Билет №8
1. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби. Дробь три четвёртых сократить нельзя, так как числа 3 и 4 взаимно простые. Такую дробь называют несократимой.
Наибольшее число, на которое можно сократить дробь, — это наибольший общий делитель ее числителя и знаменателя.
2. Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
3. 24; 64
Билет №9
1. Два числа, произведение которых равно 1, называют взаимно обратными.
2. Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Решим еще две задачи на нахождение дроби от числа.
Задача . Путешественник прошел за два дня 20 км. В первый день он прошел 0,6 всего пути. Сколько километров прошел путешественник в первый день?
3. 11
Билет №10
1. Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой, — знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть любые числа, а также числового или буквенные выражения. С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.
Пример 1. Найдем значение выражения
Решение. Умножив числитель и знаменатель этого дробного выражения на 6, получим: 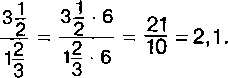
2. Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
3. Решение. Так как 2400 : 0,8 = 24 ООО : 8 = 3000, то площадь всего поля равна 3000 га.
Билет №11
1. Частное двух чисел называют отношением этих чисел. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Если значения двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин (отношением длин, отношением масс, отношением площадей и т. д.).
2. Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
Задача. Пшеницей засеяно 2400 га, что составляет 0,8 всего поля! Найдите площадь всего поля.
3. Решение. Так как 7% = 0,07, а 98 : 0,07 = 1400, то рабочий по плану (должен был сделать 1400 деталей.
Билет №12
1. Можно записать равенство 3,6 : 1,2 = 6,3 : 2,1.
Равенство двух отношений называют пропорцией.
С помощью букв пропорцию записывают так: a : b = с : d . Эти записи читают так: «Отношение а к b равно отношению с к d» или «а так относится к b, как с относится к d».
В пропорции a : b = с : d, числа a и d называют крайними членами, а числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля.
2. Длина окружности прямо пропорциональна длине ее диаметра. Поэтом для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Его обозначают греческой буквой «пи». Если обозначить длину окружности буквой С, а длину диаметра буквой то С : d = к. Поэтому С = nd.
Так как диаметр окружности вдвое больше ее радиуса, то длина окружности с радиусом г равна 2кг.
Получили другую формулу длины окружности:
С = 2п*r
3. Решение. Так как 45% = 0,45, то для решения задачи надо умножить 8 на 0,45. Получим 8 • 0,45 = 3,6. Значит, картофелем занято 3,6 га.
Билет №13
1. B верной пропорции произведение крайних членов равно произведению средних.
Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
Это свойство называют основным свойством пропорции.
Пропорция 20 : 16 = 5:4 верна, так как 20 • 4 = 16 • 5 = 80.
2. Любое отрицательное число меньше любого положительного числа. Из двух I отрицательных чисел меньше то, модуль которого больше. Нуль больше любого отрицательного числа, но меньше любого положительного числа.
Например, -7,5 | -9 |.
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. На рисунке 65 видим, что точка В (6) лежит правее точки А (-10), а точка А (-10) лежит правее точки С (-15).
-15 -10 0 6
—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I—I ►
С А О В
3. 6,85
Билет №14
1. Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Если величины обратно пропорциональны, то отношение значений одно величины равно обратному отношению соответствующих значений другой величины.
2. Прибавить к числу а число b — значит изменить число а на b единиц.
Любое число от прибавления положительного числа увеличивается, а при прибавления отрицательного числа уменьшается.
Сумма двух противоположных чисел равна нулю.
3. 20,4 т
Билет №15
1.
Участки земной поверхности изображают бумаге в уменьшенном виде. Например, отрезок 1000 м изображают на карте отрезком в 1см. Так как 1000 м = 100 000 см, то каждый отрезок на карте в 100 000 раз меньше соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
2. Чтобы сложить два числа с разными знаками, надо: 1) из большего| модуля слагаемых вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
3. 420
Билет №16
1. Футбольный мяч, глобус, арбуз дают нам представление о шаре. Все точки поверхности шара одинаково удалены от центра шара.
Отрезок, соединяющий точку поверхности шара с центром, называют радиусом шара.
Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара. Диаметр шара равен двум радиусам. Поверхность шара называют сферой.
2. Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.
Например, 8 + 3 = 11, и потому 11-8 = 3. Но 11+ (-8) тоже равно3.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a - b= a + (-b).
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.
3. 15
Билет №17
1. Прямую с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой, называют координатой этой точки.
2. Задача. Чему равна длина отрезка АВ, если А (-5) и В (9)?
Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу -5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то -5 + х = 9. Отсюда х = 9 — (-5); х = 14. Значит, длина отрезка равна 14 единичным отрезкам.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
3. 4
Билет №18
1. Точки с координатами 5 и -5 одинаково удалены от точки О находятся по разные стороны от нее. Чтобы попасть из точки О в эти точек надо пройти одинаковые расстояния, но в противоположных направления Числа 5 и -5 называются противоположными числами: 5 противоположно - а -5 противоположно 5.
Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа, противоположные им числа и нуль называют целыми числами.
2. Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак минус
Например, (-1,2) • 0,3 = -(1,2- 0,3) = -0,36;
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Например, (-3,2) • (-9) = |-3,2| • |-9| = 3,2 • 9 = 28,8. Обычно пишут короче: (-3,2) • (-9) = 3,2 • 9 = 28,8.
3. 72, 33339, 999333 – делятся на 3; 72, 999333 – делятся на 9
Билет №19
1. Расстояние до точки М (-6) от начала отсчета О равно 6 единичным отрезкам (рис. 63). Число 6 называют модулем числа -6.
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а). Модуль числа 5 равен 5, так как точка В (5) удалена от начала отсчета на 5 единичных отрезков.
2. Пишут: (-12): (-4) = | -12 |: | -4 | = 3, или короче:
(-12): (-4) = 12 : 4 = 3.
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например, -4,5: (-1,5) = 4,5 :1,5 = 3;
При делении чисел с разными знаками, надо:
1) разделить модуль делимого на модуль делителя;
2) поставить перед полученным числом знак -.
Обычно вначале определяют и записывают знак частного, а потом уж находят модуль частного.
При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!
3. Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу -5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то -5 + х = 9.
Отсюда х = 9 — (-5); х = 14.
Значит, длина отрезка равна 14 единичным отрезкам.
8