ВВЕДЕНИЕ
В 21 веке, где повсеместно используются компьютерные технологии, где калькуляторы присутствуют в наручных часах, мобильном телефоне, в компьютере, очень важным является умение быстро и рационально произвести вычисления устно, не допустив при этом ошибки. В нашей жизни учащиеся сталкиваются с такой проблемой: и в школе на уроках, особенно на математике, физике и химии, и в домашних условиях, а также в магазине.
Особенно при выполнении заданий по математике возникает необходимость научиться решать быстро и качественно, в связи с тем, что каждому ученику 9 класса необходимо сдать обязательный экзамен по математике, а на нём, как известно, не разрешается использовать калькулятор. На самом деле калькулятор на экзамене по математике не нужен. Все задачи решаются без него. Главное - внимание, аккуратность и некоторые математические приемы.
Цель данной работы: изучение некоторых рациональных приёмов вычислений и их применения при подготовке к ОГЭ по математике и в повседневной жизни.
Для достижения поставленной цели предполагается решение следующих задач:
1.Провести первичную и повторную диагностику навыков быстрого счёта у учащихся 9 класса.
2.Освоить различные приёмы быстрого счёта и научиться их использовать.
3.Провести мастер-классы «Приёмы быстрого счёта»
4.Проанализировать экзаменационные работы и демоверсии 2014-2016гг. И выбрать из них задания, в которых используются способы рациональных вычислений.
Перед исследованием мы выдвинули гипотезу, которая заключается в следующем: изучив рациональные приёмы вычислений, учащиеся смогут более успешно сдать ОГЭ по математике.
Объект исследования: использование методов и приёмов быстрого счёта для математического развития школьников.
Предмет исследования: нестандартные приёмы и навыки быстрого счёта при подготовке к ОГЭ по математике.
Данную тему мы считаем актуальной, потому что школьникам, которые на уроках привыкли производить все вычисления на калькуляторе или листочке трудно приходится на экзамене, да и в жизни.
Все учащиеся девятых классов мечтают хорошо сдать экзамен по математике. Для этого всего лишь необходимо научиться считать быстро и правильно. Ведь главная причина потери баллов на экзамене по математике- вычислительные ошибки. Гибкость ума является предметом гордости людей, а способность, например, быстро производить вычисления в уме вызывает откровенное удивление. Такие навыки помогут человеку в учёбе, в быту.
При работе пользовались следующими методами:
Поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети интернет.
Практический метод выполнения вычислений с применением рациональных приемов счета.
Анализ полученных в ходе исследования данных.
Повышение вычислительной культуры учащихся при использовании алгоритмов, рациональных вычислений ведёт к более успешной сдаче экзамена по математике. В этом заключается новизна исследования. Кроме того устный счёт развивает память, интеллектуальные способности, воспитывает ответственность, умение рационально использовать время, сконцентрироваться на задании, мотивируетк стремлению найти рациональный способ решения.
Ожидаемый результат: в результате исследования мы ожидаем, что учащиеся, изучив некоторые рациональные приёмы вычислений, а также научившись их применять, могут более успешно сдать экзамен по математике, и что самое главное - быстрота счёта всегда пригодится в повседневной жизни.
Практическая значимость: счет является простым и легким делом, когда владеешь особыми приемами и навыками. Человек, легко оперирующий цифрами, никогда не окажется обманутым при расчетах. Каждый ученик улучшит вычислительные навыки с использованием приемов быстрого счета, тем более, научившись быстро вычислять, пригодиться при выполнении контрольных работ и сдаче ОГЭ по математике. Наработка вычислительных навыков должна быть ежедневной, надо стремиться к тому, чтобы как можно больше усвоить вычислительных приемов. Простые устные упражнения могут, развить каждого из нас. Нужно только стараться и усердно работать.
ИСТОРИЯ ВОЗНИКНОВЕНИЯ СЧЁТА
Как считали в древности, какова была древняя система счета?
Изначально человеком древний счет осуществлялся только на пальцах рук и ног, то есть в пределах двадцати. Позже стали использовать различные подручные предметы: палочки, камушки, бусинки и другие. Соответственно, пределы древнего счета расширялись.
Древние ацтеки (примерно 1300 г.) уже легко могли оперировать с огромными числами. Именно им принадлежит изобретение системы исчисления с помощью какао-бобов. Зерна выкладывали в ряды (строки), в которых было не больше 19 штук.
Индейцы майя, которые пришли на смену ацтекам, также внесли значительный вклад в историю древнего счета. Кроме того, что мы знаем о них, что они составили знаменитый календарь майя, они разработали собственную систему расчетов, где использовались только точки и черточки.
А в Древнем Риме и Древней Греции была создана счетная доска – абак. Она представляла собой желобки, в которых размещались различные предметы обихода: камушки, косточки, бусы. Сама же доска выполнялась из различных известных на тот момент материалов: дерево, глина, слоновая кость и даже мрамор.А на Востоке (Китай) был аналог абака – доска суань-пан, где цифры представлены были цветными бусинками.
Еще одно средство древнего счета: собственно сами счеты. Это исконно русское изобретение. Ходят легенды, что счеты были придуманы в ХVІ веке. Во время правления Ивана Грозного его мать Елена Глинская устроила денежную реформу. Она разделила рубль на 100 копеек (это сохранилось до сих пор), и считать в уме деньги стало сложнее. 
Так мы считали вплоть до середины 20 века, потом счеты сменил арифмометр – он оставался главным орудием труда бухгалтеров до 1973 года, пока не появились современные калькуляторы. Но вот что удивительно: сложить пару 35-значных чисел, как это делали ацтеки на какао-бобах, на калькуляторе вряд ли получится.
2. ДИАГНОСТИКА НАВЫКОВ БЫСТРОГО СЧЁТА УЧАШИХСЯ
Практика показывает, что большинство учащихся допускают вычислительные ошибки, тому виной использование калькуляторов на уроках и выполнении домашних заданий. Тем более, чем старше остановиться ребёнок, тем сложнее школьная программа, сложнее становятся вычисления. Учащиеся старших классов, как известно, ленятся, не используют приёмы рациональных вычислений, даже, если их знают. Самые простые расчёты выполняют не на листочке бумаги или устно, а с помощью калькулятора, что очень негативно сказывается на экзаменах.
Перед выполнением исследовательской работы в 9 классе нами было проведено анкетирование, позволяющие выяснить, знакомы ли ученики 9 класса со способами, которые помогают упрощать вычисления, и применяют их на практике. Были предложены следующие вопросы:
Анкетирование
1.Нужно ли уметь выполнять арифметические действия с числами современному человеку?
2.Умейте ли вы умножать, вычитать, складывать числа столбиком, делить «уголком»?
3.Знакомы ли вы со способами, которые позволяют быстро производить вычисления? С какими?
4.Применяли ли вы эти способы при выполнении заданий по математике?
5.Помогают ли вам эти способы экономить время на уроке? При выполнении домашней работы?
![]()
По результатам анкетирования можно сделать вывод, что ученики 9 класса в большинстве не знают способов, которые позволяют быстро и рационально производить вычисления, редко применяют их на практике.
Лишь некоторые из них знакомы со способом умножение на 5 и 25, вычисления по формуле (а+b) (а-b) = а2 - b2.
Проанализировав ситуацию у учащихся 9 класса, мы решили изучить рациональные способы вычислений, которыми не владеем, и обучить учеников 9 класса данным способом для дальнейшего применения их на экзамене. Для этого мы разработали серию презентаций, которая позволяет обучить учащихся приёмам рациональных вычислений.
Начиная с апреля 2015 года, мы два раза в неделю ходили в 9 класс на уроки математики, показывая на примерах приёмы быстрых вычислений. Мы провели 13 уроков, отрабатывая навыки алгоритмов быстрых вычислений. После каждого занятия проводилась небольшая проверочная работа, позволяющая выяснить степень усвоения материала. Ошибки, полученные учениками в работах, в большем из случаев, связанны с невнимательностью и легкомысленным отношением к рациональным приёмам. Большинство учащихся посчитали, что для них данные занятия – пустая трата времени, не желали научиться считать быстро и рационально, объясняя это тем, что они прекрасно умеют вычислять «столбиком и уголком». Только убеждение в том, что отработка вычислительных навыков, запоминание алгоритмов быстрого счёта позволит выполнять более сложные задания, не затрачивая на него времени и умственной энергии, позволила нам обучить учащихся 9 класса. После чего учащиеся сдавали ОГЭ по математике.
Серия презентаций, которая предназначена для обучения рациональным вычислениям по большинству тем школьного курса математики, может быть использована на факультативах и элективных курсах, начиная с начальной школы.
3.ПРИЁМЫ УСТНЫХ ВЫЧИСЛЕНИЙ
В истории математики известно большое количество способов умножения, деления, сложения и т. д., отличающихся либо схемой записи, либо самим ходом вычислений. Принятые у нас обычный способ умножения и сложения «столбиком», деление «уголком», в котором многие часто допускают ошибки, является привычным для нас, но не самым удобным.
Рассмотрим несколько способов устных вычислений.
1. УМНОЖЕНИЕ
Умножение с помощью множителей числа
Найдем произведение чисел 4 и 14 с помощью множителей перемножаемых чисел. Умножим первое число на 2, а второе число разделим на 2. От этого результат не изменится.
Тогда 4 14=(4
14=(4  2)
2)  (14:2) = 8
(14:2) = 8  7 =56.
7 =56.
2. Прямое умножение
1) перемножают число десятков у множителей и к полученному результату приписывают два нуля.
2) число десятков первого множителя умножают на число единиц второго множителя и к полученному результату приписывают нуль.
3) Число единиц первого множителя умножают на число десятков второго множителя, к полученному результату приписывают нуль.
4) перемножают число единиц у множителей. Например, перемножим число десятков и к полученному результату припишем два нуля: 2  7 =1400. Умножим число десятков первого множителя (2) на число единиц второго множителя(4) и к полученному результату припишем нуль: 2
7 =1400. Умножим число десятков первого множителя (2) на число единиц второго множителя(4) и к полученному результату припишем нуль: 2  4 = 8 =80. Умножим число единиц первого множителя (6) на число десятков второго множителя (7) и к полученному результату припишем нуль: 6
4 = 8 =80. Умножим число единиц первого множителя (6) на число десятков второго множителя (7) и к полученному результату припишем нуль: 6  7 = 42 - 420. Перемножим число единиц: 6
7 = 42 - 420. Перемножим число единиц: 6  4 = 24. Тогда 26
4 = 24. Тогда 26  74 = 1400 + 80 + 420 + 24 = =1924.
74 = 1400 + 80 + 420 + 24 = =1924.
3.Умножение на125
Умножение на 125 заменяют умножением на 100 и на 11/4 (потому что 100 11/4=125). Например, 26= 26
11/4=125). Например, 26= 26 100
100 125 11/4 = 2600 + 650 = 3250.
125 11/4 = 2600 + 650 = 3250.
4. Умножение на 15
Умножение на 15 заменяют умножением на 10 и на 11/2 , (потому что
10 11/2 =15).Например, 18
11/2 =15).Например, 18 15=18
15=18 11/2
11/2 10=270.
10=270.
5. Умножение на 9
Чтобы устно умножить число на 9, приписывают к нему ноль и отнимают множимое. Например, 62 9=620 - 62=600 - 42=558.
9=620 - 62=600 - 42=558.
6. Умножение на однозначное число
Чтобы устно умножить число на однозначный множитель выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого, затем единицы и оба результата. Например, 27 8=(20+7)8=20
8=(20+7)8=20 8+7
8+7 8=160+56 =216.
8=160+56 =216.
7. Умножение на двузначное число
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Умножение на двузначное число стараются облегчить умножению на однозначное число. Например, 29 12=29(10+2)=29
12=29(10+2)=29 10+29
10+29 2=290+58= 348.
2=290+58= 348.
8. Умножение на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например, 112 4 =224
4 =224 2=448.
2=448.
Чтобы устно умножить число на 8, его трижды удваивают.
Например, 217 8 = 434
8 = 434 4=868
4=868 2=1736.
2=1736.
9. Умножение на 11/2, на 11/4
Чтобы устно умножить число на 11/2 прибавляют к множимому его половину. Например, 34 11/2 = 34 + 17=51.
11/2 = 34 + 17=51.
Чтобы устно умножить число на 11/4. Прибавляют к множимому его четверть. Например,48 11/4 =48 +12=60.
11/4 =48 +12=60.
10. Умножение на 5 и 25
Чтобы устно умножить число на 5 умножают его на  , т. е. приписывают к числу ноль и делят пополам ну можно наоборот сначала делить, потом приписать 0. Например,74
, т. е. приписывают к числу ноль и делят пополам ну можно наоборот сначала делить, потом приписать 0. Например,74 5= 740:2= 370.
5= 740:2= 370.
Чтобы устно умножить число на 25, умножают его на 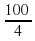 , т. е. если число кратно 4-х делят на 4 и к частному приписывают два ноля. Например,72
, т. е. если число кратно 4-х делят на 4 и к частному приписывают два ноля. Например,72 25= 72:4
25= 72:4 100= 1800.
100= 1800.
СЛОЖЕНИЕ
11. Сложение с помощью замены слагаемого
При сложении с помощью замены слагаемого одно слагаемое заменяется суммой двух чисел, чтобы дополнить другое слагаемое до круглого числа. Например,найдем сумму чисел 157 и 8 с помощью замены слагаемого. Слагаемому 157 до ближайшего круглого числа 160 не хватает 3. Поэтому представим второе слагаемое 8 в следующем виде: 8 = 3 + 5. Тогда157 + 8 = 157 + (3 + 5) = (157 + 3) + 5= 160 + 5 =165.
12. Последовательное поразрядное сложение
При последовательно поразрядном сложении к одному из слагаемых добавляют поочерёдно, начиная с высшего, все разряды второго слагаемого.
Например, найдём сумму чисел 637 и 241 методом последовательного поразрядного сложения.
637+241=637+(200+40+1)=637+200+(40+1)=837+40+1=877+1=878.
ВЫЧИТАНИЕ
13.Вычитание с помощью круглого числа
Вычитание с помощью круглого числа. Если вычитаемое оканчивается на 9, 8, 7, 6 или 5, то нужно вычесть ближайшее к вычитаемому круглое число, а к полученному результату добавить 1, 2, 3, 4 или 5 соответственно.
Например: найдем разность чисел 567 и 29 с помощью круглого числа.
567 - 29 = 567 - (30 - 1) =(567- 30) + 1 = 537 + 1 = 538.
14. Вычитание с помощью замены вычитаемого
При вычитании с помощью замены вычитаемого используют следующий прием. Вычитаемое представляют в виде суммы двух чисел, одно из которых равно цифре в разряде единиц уменьшаемого. После этого из уменьшаемого последовательно вычитают оба этих числа.
Например: у уменьшаемого 563 цифра в разряде единиц равна 3. Поэтому представим вычитаемое 8 в следующем виде: 8 = 3 + 5. Тогда
563 - 8 = 563 - (3 + 5) = (563 - 3) - 5 = 560 - 5 = 555.
ВОЗВЕДЕНИЕ В КВАДРАТ
Квадрат числа оканчивающегося на 1, на 6
При возведении числа, оканчивающегося на 1, нужно заменить эту единицу на 0, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное заменой 1 на 0.
Например, 412 = 402 +41+40= 1600 + 40 + 41=1681 = 412.
При возведении в квадрат числа, оканчивающегося на 6, нужно заменить эту цифру 6 на 5, возвести новое число в квадрат, и прибавить к этому квадрату, исходное число и число, полученное заменой 6 на 5.
Например,762 = 752 +75+76= 5625 + 75+76 = 5776 = 762.
Квадрат числа оканчивающегося на 5
Чтобы возвысить в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (8 9=72) и приписывают 25 (в нашем примере получается 7225). Еще примеры:
9=72) и приписывают 25 (в нашем примере получается 7225). Еще примеры:
252; 2 3=6= 625;
3=6= 625;
452; 4 5= 20= 2025;
5= 20= 2025;
1452; 14 15 = 210= 21025.
15 = 210= 21025.
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25.
ВЫЧИСЛЕНИЕ ПО ФОРМУЛЕ
17. Вычисления по формуле (а+b) (а-b) = а2 - b2
Пусть требуется выполнить устно умножение 52 48,мысленно представляем эти множители в виде (50+2)
48,мысленно представляем эти множители в виде (50+2) (50-2)и применяем приведенную в заголовке формулу: (50+2)
(50-2)и применяем приведенную в заголовке формулу: (50+2) (50-2)=502-22= 2496.
(50-2)=502-22= 2496.
6.ДЕЛЕНИЕ
18. Деление на 4 и на 8
Чтобы устно разделить число на 4, его дважды делят пополам.
Например:76:4 =38:2=19.
Чтобы устно разделить число на 8, его трижды делят пополам. Например:464:8=232:4=116:2=58;
516:8=258:4=129:2= 64.
7.ИЗВЛЕЧЕНИЕ ИЗ КВАДРАТНОГО КОРНЯ
19. Метод оценки
Извлечём квадратный корень из числа 4356, для этого подкоренное выражение разложим на простые множители:
 .
.
Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.
Например, надо найти  . Число под корнем – нечетное, оно не делится на 3, не делится на 5,не делится на 7. Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
. Число под корнем – нечетное, оно не делится на 3, не делится на 5,не делится на 7. Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
Очевидно, что в квадрат возводили двузначное число, которое находится между числами 70 и 80, поскольку, 702=4900, 802=6400 а число 5041 находится между ними. Первую цифру в ответе мы уже знаем, это 7.
Последняя цифра в числе 5041 равна 1. Поскольку 12=1, 92=81, последняя цифра в ответе – либо 1, либо 9. Проверим:
712=(70+1)2=4900+140+1=5041.
Существует множество способов быстрого счета, каждый может выбрать для применения наиболее простой и оригинальный.
4. ПОВТОРНАЯ ДИАГНОСТИКА НАВЫКОВ БЫСТРОГО СЧЕТА УЧАЩИХСЯ
В своей серии презентаций мы рассмотрели лишь некоторые нестандартные приёмы устных вычислений, способствующих развитию памяти и повышению математической культуры учащихся. В первую очередь, мы обращали внимание на то, что большую часть заданий при решениях, возможно, выполнять без записей на черновике или при наименьшем возможном их количестве.
После нашей работы в 9 классе, проведения экзамена по математике, была проведена повторная диагностика учащихся 9 класса, с целью выяснения использования быстрых приемов счета на ОГЭ по математике.
Анкетирование
1.Пользовались ли вы способами, которые позволяют быстро производить вычисления на экзамене?
2.Считаете ли вы, что данные способы помогли вам сэкономить время при выполнении экзаменационной работы?
3. Действительно ли, знание рациональных приемов и их применение важно, когда учащийся не имеет таблиц или калькулятора?
![]()
Результаты получились следующие: учащиеся 9 класса старались пользоваться уже привычными для них алгоритмами вычислений, знакомыми из начальной школы, производя практически все действия в письменном виде, чтобы уж, наверняка, не допустить ошибок при решении заданий.
Менее половины учащихся посчитали, что ускоренные способы счета пригодились им при выполнении экзаменационной работы, что позволило сэкономить время на экзамене.
Часть учащихся ответили, что они недостаточно прочно усвоили приемы рациональных вычислений, не хватило времени на наработку вычислительных навыков. Поэтому, мы решили создать памятку «Быстрый счет», для использования ее на каждом уроке математики для рациональных вычислений при выполнении заданий (Приложение 1). Успешное овладение приемами устных вычислений должно быть не механическое, а вполне сознательное, кроме того, иметь более или менее продолжительную тренировку. Зато, усвоив ускоренные приемы, можно выполнить быстрые расчеты в уме с безошибочностью письменных вычислений. А так же мы сравнили показатели итоговой аттестации 2014 и 2015 года, и пришли к выводу, что одной из причин повышения качества знаний послужило применение на экзамене приемов устных вычислений учащимися.
![]()
Некоторые из учеников все же посчитали, что вычисления показались им сложными для подсчета в уме, поэтому они использовали известные им операции. Исходя из этого, мы решили проанализировать несколько демоверсий и тренировочных работ по математике и выяснить, действительно ли использование быстрого счета не предусматривает решения заданий устно.
5. ПРИМЕНЕНИЕ СПОСОБОВ БЫСТРОГО СЧЁТА НА ЭКЗАМЕННАЦИОННЫХ ИСПЫТАНИЯХ.
Рассмотрим несколько заданий из ОГЭ 2014-2016 года.
1.Демонстрационный вариант ОГЭ 2016 года (Приложение 2).
1.1. Задание №11. Найдите площадь трапеции изображенной на рисунке.
Решение: чтобы найти площадь трапеции необходимо воспользоваться формулой , с помощью приема «Умножение на двузначное число, находим площадь фигуры:
, с помощью приема «Умножение на двузначное число, находим площадь фигуры:
.
Ответ:168 см2.
1.2. Задание №10: Найдите длину хорды окружности радиусом 13см , если расстояние от центра окружности до хоры равно 5см. Ответ дайте в см.
Решение: для решения задачи необходимо рассмотреть прямоугольный треугольник и найти в нем катет по теореме Пифагора.
b2=132-52, вычисления произведём по формуле (а+b) (а-b) = а2 - b2
b2=(13-5)(13+5)=8 18=8
18=8 (20-2)=160-16=144, b=12. При вычислении можно было использовать прием «Умножение на 8», но он намного длиннее ,чем предложенный выше. Для нахождения хорды остаётся рассмотреть равнобедренный треугольник и доказать, что расстояние от центра окружности до хорды есть медиана в треугольнике. Следовательно, хорда равна 12
(20-2)=160-16=144, b=12. При вычислении можно было использовать прием «Умножение на 8», но он намного длиннее ,чем предложенный выше. Для нахождения хорды остаётся рассмотреть равнобедренный треугольник и доказать, что расстояние от центра окружности до хорды есть медиана в треугольнике. Следовательно, хорда равна 12 2= 24см.
2= 24см.
Ответ:24 см.
1.3. Задание №20. Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T=2 l, где l- длина нити (в метрах), пользуясь этой формулой , найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
l, где l- длина нити (в метрах), пользуясь этой формулой , найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение: для нахождения длины нити необходимо произвести следующие действия:
T=2 l , 3=2
l , 3=2 l,
l,  l=
l= ,
,  ,5 , l=1,52=2,25
,5 , l=1,52=2,25
При выполнении данного задания можно воспользоваться приёмом «Возведение числа в квадрат оканчивающимся на 5».
Чтобы вычислить 152 необходимо число десятков умножить на число, равное числу десятков плюс единица и дописать к получившемуся произведению число 25, то есть 1 (1+1)=1
(1+1)=1 2и дописываем 25.Получившееся число – 225.
2и дописываем 25.Получившееся число – 225.
Ответ:2,25.
2. Демонстрационный вариант ОГЭ 2014 года (Приложение 3).
2.1. Задание №10. К окружности с центром в точке Oпроведены катеты AB и секущая AO. Найдите радиус окружности, если AB=12см,AO=13см.
Решение: необходимо рассмотреть прямоугольный треугольник AOB и найти в нем катет OBпо теореме Пифагора.
b2=132-122, вычисления произведём по формуле (а+b) (а-b) = а2 - b2
b2=(13-12)(13+12)=1 25=25, следовательно b=5, а это и есть радиус окружности.
25=25, следовательно b=5, а это и есть радиус окружности.
Ответ: 5 см.
3.Демонстрационный вариант ОГЭ 2015 года (Приложение 4).
3.1.Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
Решение:1)198:2=99 (рублей) стоимость проезда школьника.
2)198 4=792 (рублей) стоимость проезда 4 взрослых.
4=792 (рублей) стоимость проезда 4 взрослых.
3)99 12=1188 (рублей) стоимость проезда 12 детей.
12=1188 (рублей) стоимость проезда 12 детей.
4)1188+792=1980 (рублей) стоимость проезда детей и взрослых вместе.
Устно умножая 198 на 4 , можно воспользоваться способом «Умножение на 4», 198 4=198
4=198 2
2 2=(200-2)2
2=(200-2)2 2=396
2=396 2=(400-4)2=800-8=792, либо способом «Умножение на однозначное число» 198
2=(400-4)2=800-8=792, либо способом «Умножение на однозначное число» 198 4=(200-2)4=800-8=792, второй способ проще, чем первый.
4=(200-2)4=800-8=792, второй способ проще, чем первый.
Чтобы устно умножить 99 на 12 необходимо число 99 представить в виде разности (100-1), то есть воспользоваться способом «Умножение на двузначное число» 99 12=(100-1)12=1200-12=1188.
12=(100-1)12=1200-12=1188.
Ответ:1980 рублей.
4. ОГЭ по математике вариант №101.
4.1.Задание №10. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Решение: рассмотрим прямоугольный треугольник т.к. расстояние от центра окружности до хорды есть длина перпендикуляра, и найдём в нем гипотенузу по теореме Пифагора: c2=a2+b2. При этом удобно воспользоваться способом «Возведение в квадрат числа, оканчивающегося на 5» и формулой (a+b)2= a2 + 2ab + b2.
с2=362+272=(35+1)2+(25+ 2)2=352+2 35
35 1+12+252+2
1+12+252+2 25
25 2+22=
2+22=
=1225+70+1+625+100+4=2025, то есть c=45, а это есть радиус окружности, следовательно, диаметр равен 45 2=90.
2=90.
Ответ: 90.
4.2. Задание №16. Магазин детских товаров закупает погремушки по оптовой цене 230 рублей за одну штуку и продаёт с 25- процентной наценкой. Сколько рублей будут стоить 3 такие игрушки, купленные в этом магазине?
Решение: воспользуемся способом «Деление на 4»
1)230:4=(230:2):2=115:2=57,5 (рублей) составляет 25%.
2)230+57,5=287,5(рублей) цена в этом магазине.
В последнем действии применим способ «Умножение на однозначное число».
3)287,5 3=(200+80+7+0,5)
3=(200+80+7+0,5) 3=600+240+28+1,5=869,5(рублей) цена 3 игрушек.
3=600+240+28+1,5=869,5(рублей) цена 3 игрушек.
Ответ: 869,5
4.3. Задание №17. Какое наибольшее количество коробок в форме прямоугольного параллелепипеда размером 20 50
50 100(см) можно поместить в кузов машины размером 5
100(см) можно поместить в кузов машины размером 5 2,5
2,5 3(м).
3(м).
Решение: переведём размеры коробки в (м): 0,2 0,5
0,5 1(м).
1(м).
0,2 0,5
0,5 1=0,1(м3) объем коробки.
1=0,1(м3) объем коробки.
Применим способ «Умножение на 2 »:, «Умножение на однозначное число».
»:, «Умножение на однозначное число».
5 2,5
2,5 3=(5
3=(5 2+5:2)
2+5:2) 3=(10+2,5)
3=(10+2,5) 3=30+7,5=37,5(м3) объем кузова.
3=30+7,5=37,5(м3) объем кузова.
37,5:0,1 =375(коробок).
Ответ:375 коробок.
4.4. Часть 2, задание №22. Первые 4 часа автомобиль ехал со скоростью 50км/ч, следующие 4 часа – со скоростью 80 км/ч, а последние 4 часа – со скоростью 35км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение: при нахождении устно всего расстояния, применим способ «Умножение на 4»
1)50 4+80
4+80 4+35
4+35 4=200+320+70
4=200+320+70 2=660(км)весь путь.
2=660(км)весь путь.
2)4+4+4=12(ч) всё время.
Воспользуемся способом «Деление на 4», для этого представим число 12 в виде множителей 3 и 4:
3)660:12=660:(3 4)=660:3:4=220:4=220:2:2=110:2=55(км/ч) средняя скорость автомобиля.
4)=660:3:4=220:4=220:2:2=110:2=55(км/ч) средняя скорость автомобиля.
Ответ:55 км/ч.
5.ОГЭ по математике вариант №102.
5.1.Задание №9 Катеты прямоугольного треугольника равны 
6  11 и 2 найдите синус наименьшегоугла этого треугольника.
11 и 2 найдите синус наименьшегоугла этого треугольника.
Решение: По теореме Пифагора найдём гипотенузу
(6 11)2 +22=36
11)2 +22=36 11+4=360+36+4=396+4=400, следовательно, гипотенуза равна 20. Найдём синус наименьшего числа:
11+4=360+36+4=396+4=400, следовательно, гипотенуза равна 20. Найдём синус наименьшего числа:  =
= =0,1.
=0,1.
При решении можно воспользоваться способом «Умножение на 11» либо «Умножение на двузначное число»: 36 10+36
10+36 1=396.
1=396.
Ответ:0,1
5.2. Задание №11.
На стороне BC прямоугольника ABCD у которого AB= 70 и AD=94, отмечена точка Е так, что =450. НайдитеED.
=450. НайдитеED. Решение:так как АЕ является биссектрисой, то она отсекает от прямоугольника равнобедренный треугольник, следовательно, АВ=ВЕ=70. Тогда СЕ=94-70=24. Найдём DEиз прямоугольника по теореме Пифагора:
DE2=242+702=(25-1)2+702=625-2 25
25 1+1+4900=
1+1+4900=
=626-50+4900=576+4900=5476, DE=74. При возведении в квадрат числа 24 удобно воспользоваться формулой (a-b)2= a2 - 2ab + b2, но при нахождении DE необходимо извлечь квадратный корень и числа 5476, то есть применить метод оценки: число 5476 находится между 702=4900 и 752=5625, а так как оно оканчивается на 6, то это число 74.
Ответ:74.
5.3 Задание № 17.
Лестница соединяет точки A и B. Высота каждой ступени равна 28 см, а длина – 96 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, накоторую поднимается лестница (в метрах). Решение: рассмотрим прямоугольный треугольник, в котором известны катеты, равные 28 и 96, найдём гипотенузу по теореме Пифагора.с2=282+962=(30-2)2+(100-4)2=(900-2 2
2 30+4)+(10000-2
30+4)+(10000-2 4
4 100-16)=784+9216=10000, следовательно гипотенуза равна 100 см. Найдём количество ступеней 1500:100=15, вычислим высоту лестницы воспользовавшись способом «Умножение на 15»28
100-16)=784+9216=10000, следовательно гипотенуза равна 100 см. Найдём количество ступеней 1500:100=15, вычислим высоту лестницы воспользовавшись способом «Умножение на 15»28 15=280+140=420см.
15=280+140=420см.
Ответ:420см.
5.4. Часть 2. Задание № 24. Катеты прямоугольного треугольника равны 15 и 20. Найти высоту, проведённую к гипотенузе.
Решение: через теорему Пифагора найдем гипотенузу с2=202+152=400+225=625, тогда с=25. Воспользовались способом «Возведение числа в квадрат, оканчивающегося на 5».
Найдём площадь прямоугольного треугольника:S= 20
20 15=10
15=10 15=150, площадь треугольника можно найти используя формулу S=
15=150, площадь треугольника можно найти используя формулу S= h
h а.S=
а.S= h
h 25,
25,
150= h
h 25,
25,
 h=150:25,
h=150:25,
 h=6,
h=6,
h=12
Ответ:12см.
Рассматривая и решая демонстрационные и экзаменационные работы по математике, мы пришли к выводу: многие задания из КИМов решаются устно, не выполняя письменных вычислений. Те задания, которые всё же требуют записи решений, можно выполнить, применяя рациональные способы вычислений, которые мы рассмотрели.
ЗАКЛЮЧЕНИЕ
Работая над темой исследования, мы нашли и изучили лишь некоторые рациональные приемы вычислений, которые содействуют быстрому счету. Поэтому мы считаем, что дальнейшее их изучение - тема перспективная. Для безошибочных вычислений нужна постоянная вычислительная тренировка. Из урока в урок. Она поможет приобрести полезные навыки устного счета. А научившись применять их, можно более успешно подготовиться к сдаче экзамена по математике, что также необходимо и в повседневнойжизни.
В ходе проделанной работы, мы выяснили, что, ускоренные способы счета пригодились учащимся при выполнении экзаменационной работы, что позволило сэкономить время на экзамене и улучшило качество знаний.
Также, работая над темой, мы пришли к выводу: многие задания из КИМов решаются устно, не выполняя письменных вычислений. Те задания, которые всё же требуют записи решений, можно выполнить, применяя устные способы вычислений.
Поэтому считаем, что работа, проведенная нами, доказывает, что знание приёмов рациональных вычислений и их применение особенно важно в тех случаях, когда учащийся не имеет в своём распоряжении таблиц или калькулятора. А также, мы решили, продолжить изучение рациональных вычислений с учащимися девятого класса в последующих годах для более успешного выполнения ЕГЭ по математике в 11 классе.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК И ИНТЕРНЕТ-РЕСУРСЫ
1.Просветов Г.И. Быстрый счёт: Задачи и решения.-М. АСТ: Астрель, Владимир: ВКТ, 2008.-90,[6] с.
2.Перельман Яков. Быстрый счет. Тридцать простых приемов устного счета. –:Дом занимательной науки, Ленинград, 1941.
3.http://www.1tv.ru/sprojects_utro_video/si33/p10054
4.http://repetitor-problem.net/drevniy-schet
5.http://kopilkaurokov.ru/matematika/prochee/mietodichieskoie-posobiie-po-matiematikie-osnovnyie-priiomy-bystrogho-schiota
6.http://ege-study.ru/materialy-ege/bystryj-schet-bez-kalkulyatora-i-bez-vychislitelnyx-oshibok/
Приложение 1
8
 12=29(10+2)=29
12=29(10+2)=29
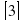
 14=(4
14=(4 
 , т. е. приписывают к числу ноль и делят пополам ну можно наоборот сначала делить, потом приписать 0. Например,74
, т. е. приписывают к числу ноль и делят пополам ну можно наоборот сначала делить, потом приписать 0. Например,74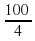 , т. е. если число кратно 4-х делят на 4 и к частному приписывают два ноля. Например,72
, т. е. если число кратно 4-х делят на 4 и к частному приписывают два ноля. Например,72