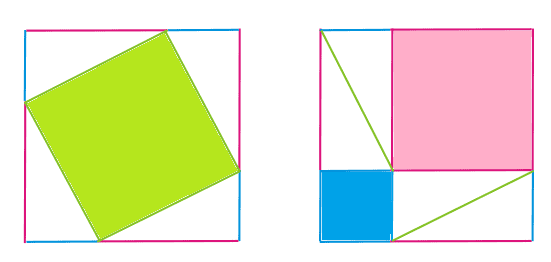
Цели: Формировать умения замечать различные особенности геометрических фигур, делать выводы из замечательных особенностей.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Конспект внеклассного занятия по математике на тему: "Геометрический тренинг"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект внеклассного занятия по математике на тему: "Геометрический тренинг"»
Полезное для учителя
Распродажа видеоуроков!
1450 руб.
2070 руб.
1310 руб.
1870 руб.
1490 руб.
2130 руб.
1650 руб.
2350 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
500 руб.
2500 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

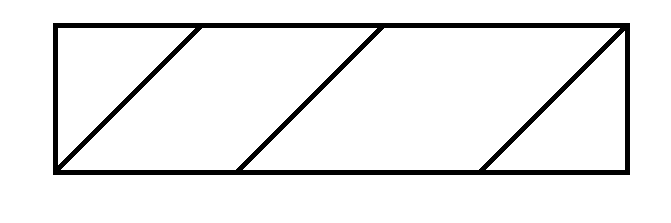
 адание №3.
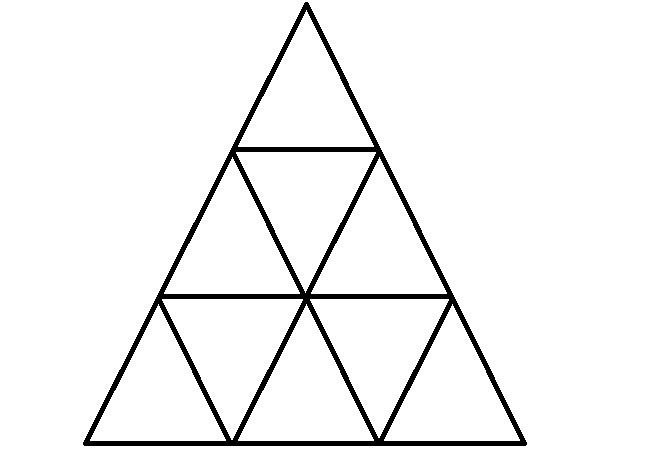
адание №3. адание №4.
адание №4.