К вопросу о методах решения задач в 5-6 классах. В статье рассмотрены несколько задач, решенных различными методами и способами. Решение любой задачи по математике определяется выбором метода ее решения. Как правило, на уроках учителем рассматривается лишь один метод решения задачи. Среди методов решения задач можно выделить: арифметический, алгебраический, практический, табличный, геометрический, смешанный метод, а также метод проб и ошибок.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
К ВОПРОСУ О МЕТОДАХ РЕШЕНИЯ ЗАДАЧ В 5-6 КЛАССАХ
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«К ВОПРОСУ О МЕТОДАХ РЕШЕНИЯ ЗАДАЧ В 5-6 КЛАССАХ»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
1670 руб.
2380 руб.
1680 руб.
2400 руб.
1680 руб.
2400 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
 , OD – луч, проведенный внутри него. Сколько градусов содержит угол DOK, если градусная мера угла NOD на
, OD – луч, проведенный внутри него. Сколько градусов содержит угол DOK, если градусная мера угла NOD на  больше градусной меры угла DOK.
больше градусной меры угла DOK. 
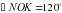 ,
,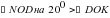
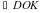
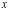 –
–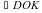 . Так как по условию
. Так как по условию 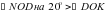 тогда,
тогда, 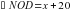 .
.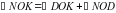 ,
, 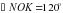
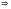 составим уравнение:
составим уравнение:  .
.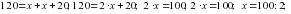
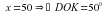
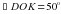 .
. . Так как по условию
. Так как по условию 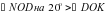 тогда,
тогда,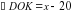 .
. 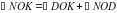 ,
, 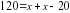 .
.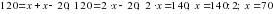
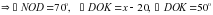
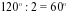 − угол, на который мог бы разбить луч OD в случае, если бы он являлся биссектрисой;
− угол, на который мог бы разбить луч OD в случае, если бы он являлся биссектрисой;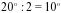 − разница, на сколько каждый угол отличается от половины данного угла;
− разница, на сколько каждый угол отличается от половины данного угла; −
−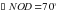 ;
;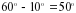 −
− .
.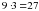 (м) ткани требуется на три платья и три сарафана;
(м) ткани требуется на три платья и три сарафана;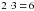 (м) ткани требуется на три сарафана;
(м) ткани требуется на три сарафана;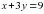 . Т.к. три таких же платья и пять сарафанов ушло 19м, следовательно
. Т.к. три таких же платья и пять сарафанов ушло 19м, следовательно 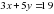 . Составим систему линейных уравнений:
. Составим систему линейных уравнений: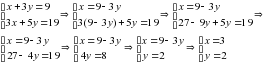
 , а три сарафана – тремя отрезками
, а три сарафана – тремя отрезками  . Все четыре отрезка будут моделировать количество ткани, использованное для пошива платья и трёх сарафанов, то есть 9 м. Ниже смоделируем соответствующими отрезками условие задачи, что на три таких же платья и пять сарафанов потратили 19 м. Так как во втором условии задачи платьев в три раза больше, чем в первом условии, то в третьей строке начертим три фигуры первой строки, получим три отрезка характеризующих платья и девять отрезков показывающий сарафаны общей условной длиной 27м.
. Все четыре отрезка будут моделировать количество ткани, использованное для пошива платья и трёх сарафанов, то есть 9 м. Ниже смоделируем соответствующими отрезками условие задачи, что на три таких же платья и пять сарафанов потратили 19 м. Так как во втором условии задачи платьев в три раза больше, чем в первом условии, то в третьей строке начертим три фигуры первой строки, получим три отрезка характеризующих платья и девять отрезков показывающий сарафаны общей условной длиной 27м. 
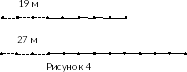
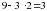 . Таким образом, мы ответили на главные вопросы задачи: 3м ткани требуется на одно платье и 2м на один сарафан.
. Таким образом, мы ответили на главные вопросы задачи: 3м ткани требуется на одно платье и 2м на один сарафан.



















