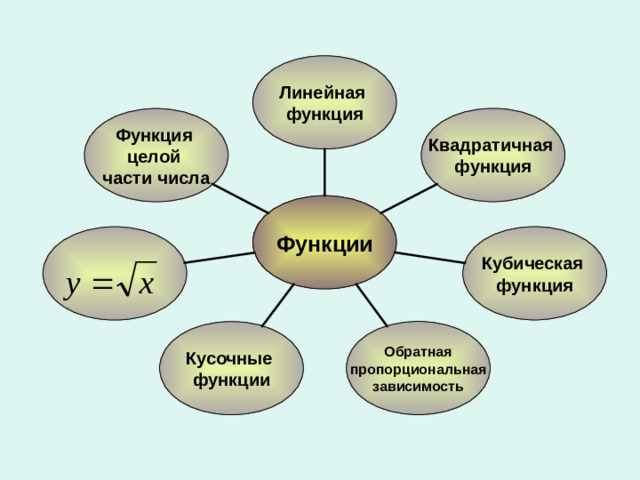
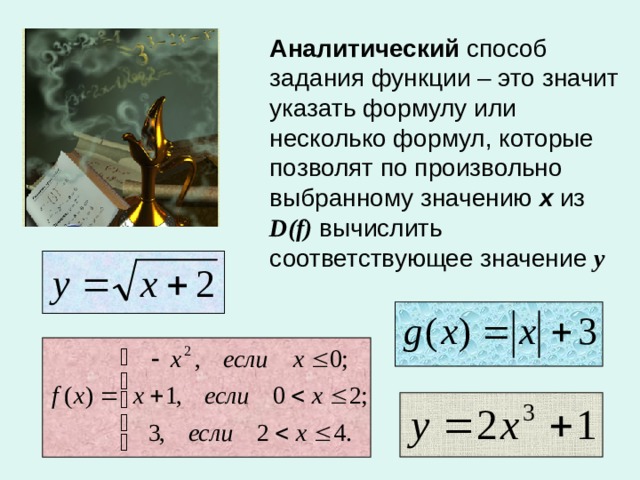
Определение.
Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят задана функция у = f (x) с областью определения Х;
пишут у = f (x) , х Х
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Мастер-класс «Изучение числовых функций, их свойств и графиков»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Мастер-класс «Изучение числовых функций, их свойств и графиков»»
Полезное для учителя
Распродажа видеоуроков!
1450 руб.
2070 руб.
1650 руб.
2350 руб.
1850 руб.
2640 руб.
1650 руб.
2350 руб.
Курсы ПК и ППК для учителей!
2760 руб.
13800 руб.
3560 руб.
17800 руб.
800 руб.
4000 руб.
600 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


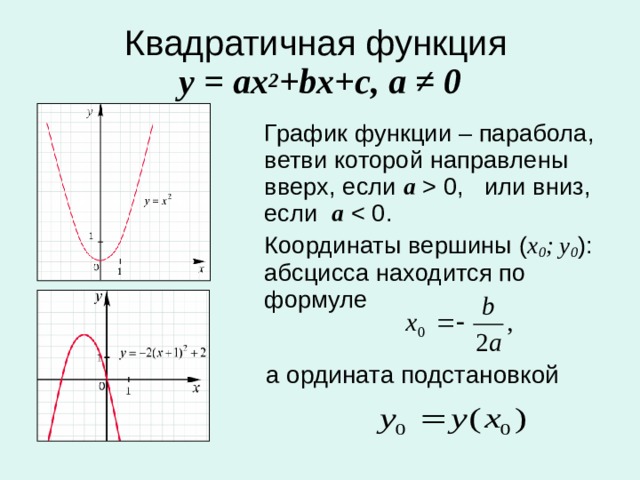 0 , или вниз, если а Координаты вершины ( х 0 ; у 0 ): абсцисса находится по формуле а ордината подстановкой" width="640"
0 , или вниз, если а Координаты вершины ( х 0 ; у 0 ): абсцисса находится по формуле а ордината подстановкой" width="640"
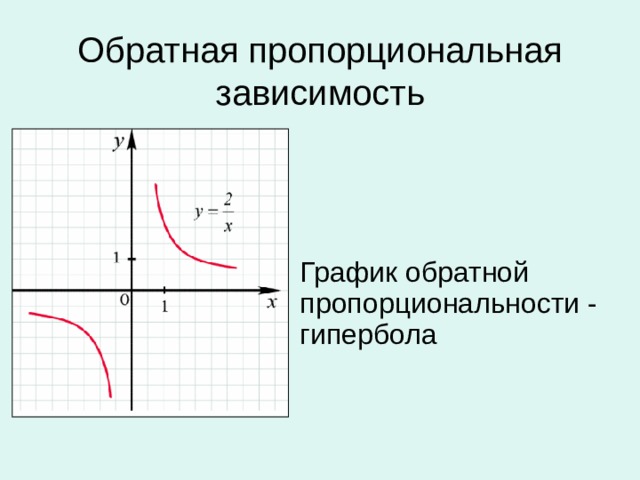
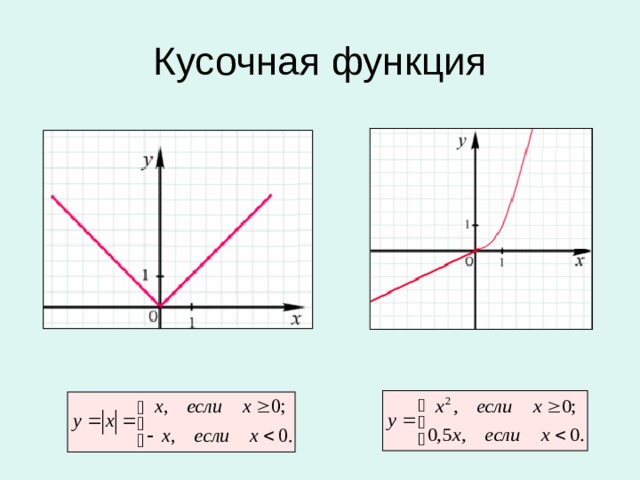
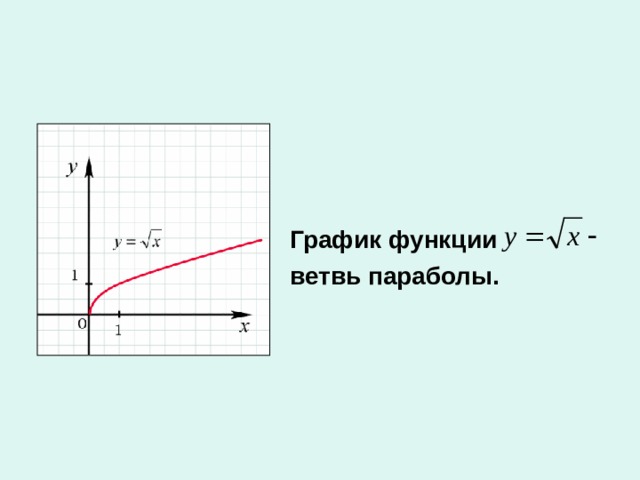
![Функция целой части числа у = [ x ] D ( у ) = ( - ∞; + ∞) E ( у ) = Z](https://fsd.kopilkaurokov.ru/up/html/2020/01/09/k_5e16f5c7bf615/img_user_file_5e16f5c96ccba_9.jpg)
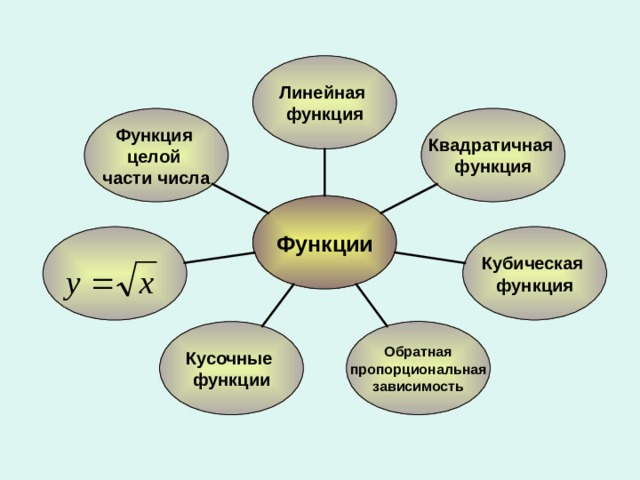



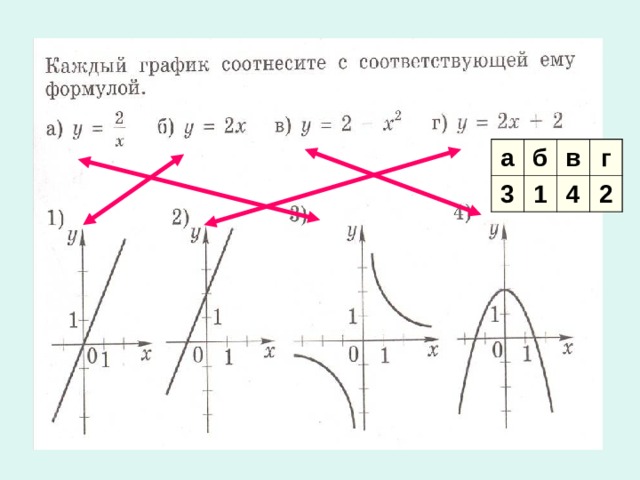
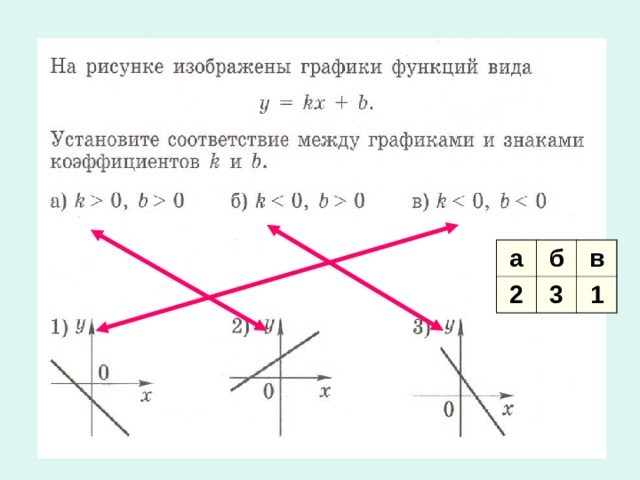

 6 или D (y) = ( 6 ; + ∞ ) Да Нет Е(у) : у ≥ -3 или Е(у)= [-3 ; + ∞) Прямая" width="640"
6 или D (y) = ( 6 ; + ∞ ) Да Нет Е(у) : у ≥ -3 или Е(у)= [-3 ; + ∞) Прямая" width="640"



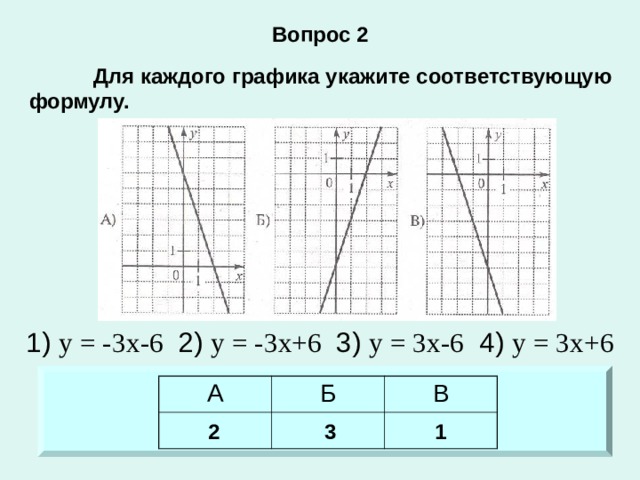

![Вопрос 4 На рисунке изображен график функции, заданной на промежутке [ -5; 4). Укажите множество значений этой функции. 1) [-5; 4) 2) [-3; 2) 3) [-3; 3] 4) [-3; 2) U (2; 3]](https://fsd.kopilkaurokov.ru/up/html/2020/01/09/k_5e16f5c7bf615/img_user_file_5e16f5c96ccba_27.jpg)
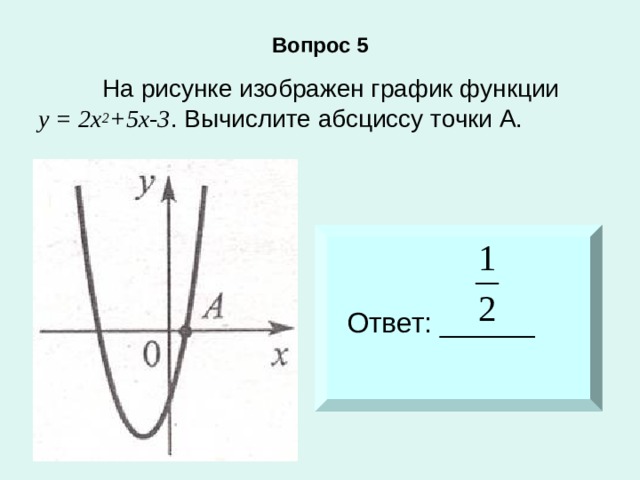
![Вопрос 6 На рисунке изображен график функции у = f (х), заданный на промежутке [ -1; 4,5 ] . Из приведенных ниже утверждений выберите верное. Наименьшее значение функции у = f (х) равно 0. 2) f (х) при -0,5 3) Функция у = f (х) возрастает на промежутке [ -1; 1 ] 4) f (0) = 3](https://fsd.kopilkaurokov.ru/up/html/2020/01/09/k_5e16f5c7bf615/img_user_file_5e16f5c96ccba_29.jpg)
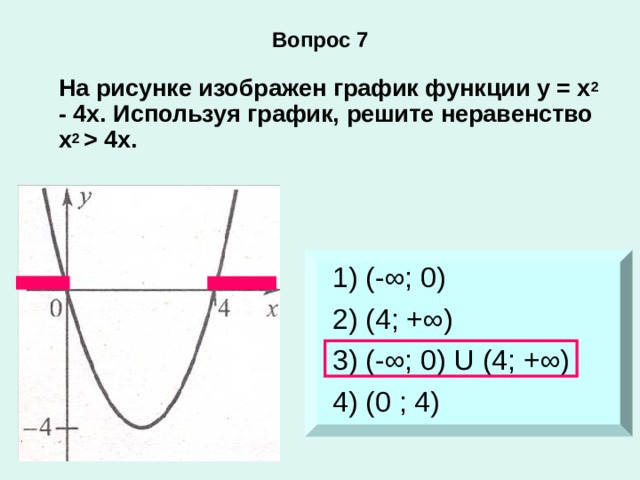 4 х. 1) (- ∞; 0) 2) (4; + ∞) 3) (- ∞; 0) U (4; + ∞) 4) (0 ; 4)" width="640"
4 х. 1) (- ∞; 0) 2) (4; + ∞) 3) (- ∞; 0) U (4; + ∞) 4) (0 ; 4)" width="640"
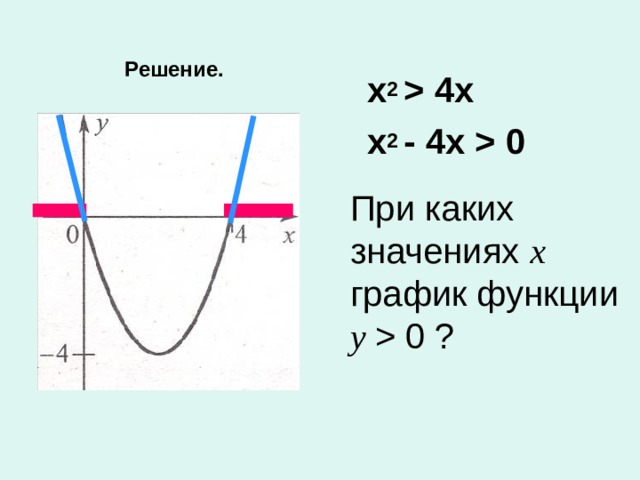 4х х 2 - 4х 0 При каких значениях х график функции у 0 ?" width="640"
4х х 2 - 4х 0 При каких значениях х график функции у 0 ?" width="640"

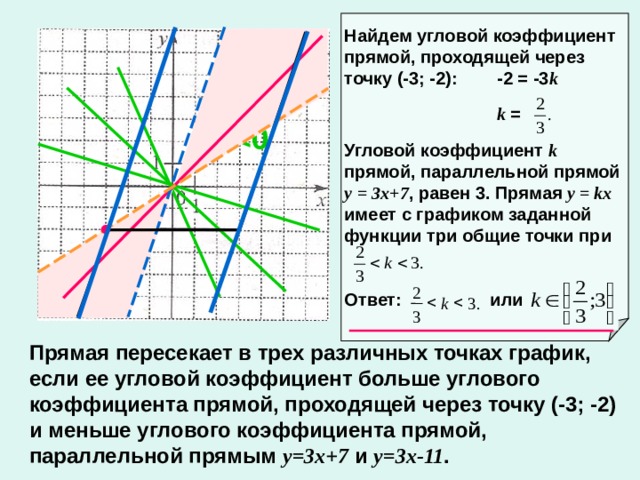 0. 2 . 3 k 3 Прямая пересекает в трех различных точках график, если ее угловой коэффициент больше углового коэффициента прямой, проходящей через точку (-3; -2) и меньше углового коэффициента прямой, параллельной прямым у=3х+7 и у=3х-11 ." width="640"
0. 2 . 3 k 3 Прямая пересекает в трех различных точках график, если ее угловой коэффициент больше углового коэффициента прямой, проходящей через точку (-3; -2) и меньше углового коэффициента прямой, параллельной прямым у=3х+7 и у=3х-11 ." width="640"





















