«Развитие познавательной и творческой активности учащихся через технологию проблемного обучения»
Цель: показать развитие познавательной и творческой активности учащихся через технологию проблемного диалога, создание проблемных ситуаций на уроке.
Ход занятия:
Одна из серьезных проблем современной школы - нежелание большинства учащихся учиться. Такое состояние порождает ряд других не менее катастрофических проблем:
• усиливается репрессивная, принудительная составляющая учебного процесса, что вызывает еще большее отторжение учения;
• подавляются творческие начала, разрушаются личностные качества учащихся.
Сегодня мне хотелось бы представить вам в действии технологию проблемного диалога. Она даёт возможность учителю создать условия, для того чтобы ученик сам добывал знания, учился самостоятельно решать поставленные перед ним задачи. Всё это позволяет обучать ребёнка в режиме деятельностного подхода. Что соответствует требованиям стандартов нового поколения. А учитель, как образно замечает Л.С.Выготский, “… должен быть рельсами, по которым свободно и самостоятельно движутся вагоны, получая от них только направление собственного движения».
Т.е. учитель играет роль режиссёра учебного процесса. Он мотивирует школьников к самостоятельному принятию решения. Корректирует их действия. Участвует в обсуждении и ищет способы, чтобы включить в работу каждого ученика. Это в целом ведёт к формированию УУД: личностных, коммуникативных, познавательных и регулятивных.
Эпиграфом к современному обучению может служить стихотворения Н .Рыленкова «Урок как дорога в будущее»
Пока идёшь за кем-то вслед,
Дорога не запомнится.
Зато, куда б ты не попал,
И по какой распутице
Дорога та, что сам искал
Вовек не позабудется.
К сожалению, очень часто учитель не предоставляет свободы ученику, когда он пытается ответить на вопрос. Учитель не ждёт, сразу же задаёт другой наводящий вопрос. Можно ли учить так, чтобы каждый ребёнок рассуждал над проблемой своим путём, своим темпом, но при необходимости мог сопоставить свою точку зрения с одноклассниками, может даже изменить её? Да, можно. Проанализировав ситуацию в классах, где веду математику, пришла к выводу: Математика начинается вовсе не со счета, что кажется очевидным, а с…загадки, проблемы.
Помочь ученику раскрыться, лучше использовать свой творческий потенциал помогает создание проблемных ситуаций на уроке.
Проблемное обучение – это «начальная школа» творческой деятельности.
Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.
Технологию проблемного диалога можно применять при изучении любой школьной дисциплины и на любой образовательной ступени и потому необходима каждому учителю.
Что нужно учителю для освоения технологии?
Всего две вещи нужны учителю для осознанного освоения технологии проблемного диалога: знания и желание их применять.
АВТОРОМ ЭТОЙ ТЕХНОЛОГИИ ЯВЛЯЕТСЯ Мельникова Елена Леонидовна
Из каких этапов состоит проблемно-диалогический урок?
Этапы урока по технологии проблемного диалога
1. Создание проблемной ситуации учителем и формулирование учебной проблемы учениками.
2. Выдвижение версий решения проблемы.
3. Актуализация имеющихся знаний.
4. Составление плана решения проблемы.
5. Поиск решения проблемы – открытие нового знания.
6. Выражение решения проблемы и применение нового знания на практике.
!!! Модель не жёсткая. В рамках каждой темы возможны существенные вариации при сохранении основных этапов.
Я сегодня остановлюсь на первом этапе: создание проблемной ситуации учителем и формулирование учебной проблемы учениками. Для меня в процессе обучения главным является постановка перед учащимися на уроках небольших проблем и стремление решить их вместе с детьми.
Как же создавать проблемные ситуации? Об этом мы сегодня и поговорим.
Проблемная ситуация — состояние умственного затруднения, вызванного в определенной учебной ситуации объективной недостаточностью ранее усвоенных учащимися знаний и способов умственной и практической деятельности для решения возникшей познавательной задачи.
Типы проблемной ситуации: с удивлением и с затруднением
Ученик должен сформулировать проблему. А учитель должен создать для этого условия. А делает он это с помощью двух диалогов.
Виды диалогов
Побуждающий диалог
Вопросы учителя, побуждающие детей высказывать различные версии решения проблемы
Подводящий диалог
Цепочка вопросов, последовательно приводящих к правильному ответу, запланированному учителем
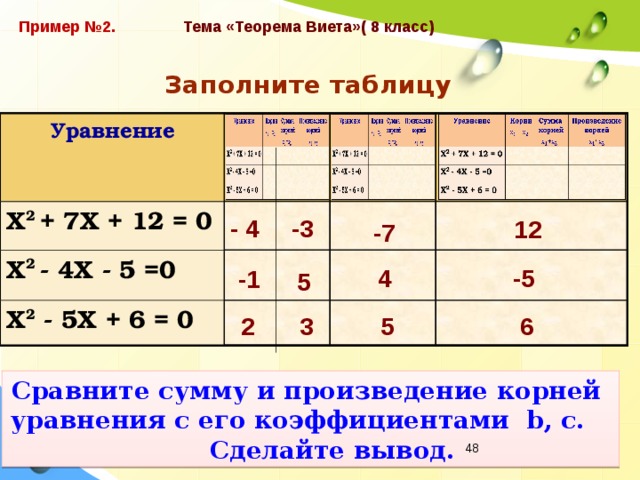
ПО МНЕНИЮ АВТОРОВ технологии, побуждающий и подводящий диалоги имеют достоинства и недостатки.
Побуждающий диалог
Вопросы учителя, побуждающие детей высказывать различные версии решения проблемы
+ Развивает творческое мышление.
+ Максимально близок к жизненным ситуациям.
- Ученики могут увести в сторону от темы.
- Невозможно рассчитать время на уроке.
Подводящий диалог
Цепочка вопросов, последовательно приводящих к правильному ответу, запланированному учителем
+ Развивает логическое мышление.
+ Просчитывается по времени.
+ Ведет к нужному результату коротким путем.
- В меньшей степени развивает творчество и инициативу.
Сегодня я остановлюсь на побуждающем диалоге. Чтоб создать его, учитель использует следующие приёмы (их 4)
Приёмы создания проблемной ситуации
Прием 1. Проблемная ситуация с противоречивыми положениями создается одновременным предъявлением классу противоречивых фактов, теорий, мнений. В данном случае факт понимается как единичная научная информация, теория – система научных взглядов, мнение – позиция отдельного человека. Побуждение к осознанию противоречия осуществляется репликами: «Что вас удивило? Что интересного заметили? Какое противоречие налицо?».
Прием 2. Проблемная ситуация со столкновением мнений учеников класса создается вопросом или практическим заданием на новый материал. Побуждение к осознанию противоречия осуществляется репликами: «Вопрос был один? А мнений сколько?» или «Задание было одно? А выполнили вы его как?». И далее общий текст: «Почему так получилось? Чего мы еще не знаем?».
Прием 3. Проблемная ситуация с противоречием между житейским (т.е. ограниченным или ошибочным) представлением учеников и научным фактом создается в два шага. Сначала (шаг 1) учитель выявляет житейское представление учеников вопросом или практическим заданием «на ошибку». Затем (шаг 2) сообщением, экспериментом, расчетами или наглядностью предъявляет научный факт. Побуждение к осознанию противоречия осуществляется репликами: «Вы что думали сначала? А что оказывается на самом деле?».
Прием 4. Проблемная ситуация с противоречием между необходимостью и невозможностью выполнить задание учителя создается практическим заданием, не сходным с предыдущим. Побуждение к осознанию проблемы осуществляется репликами: «Вы смогли выполнить задание? В чем затруднение? Чем это задание не похоже на предыдущее?».
Предлагаю следующие варианты создания проблемных ситуаций на уроках математики.
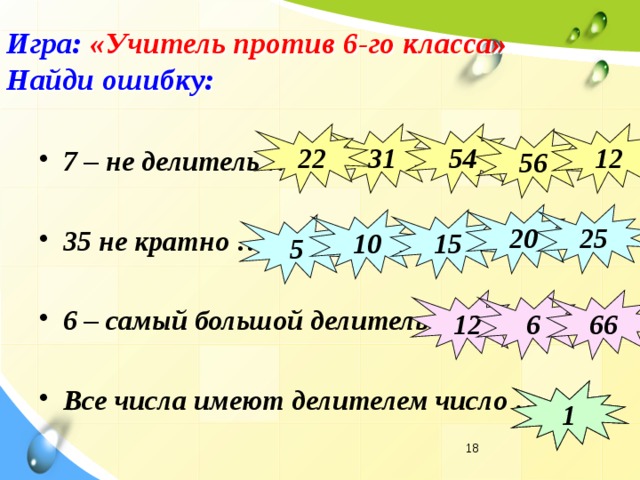
1. Создание проблемных ситуаций через умышленно допущенные учителем ошибки.
В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение.
Пример №1. Тема «Линейные уравнения с одной переменной». (7 класс)
Решаю быстро уравнение:
(3Х + 7) • 2 – 3 = 17
6Х + 14 – 3 = 17
6Х = 17 – 14 – 3
6Х = 0
Х = 0
Естественно при проверке ответ не сходится Проблемная ситуация. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат - внимательность и заинтересованность на уроке.
Пример №2. «Обманные задачи»:
а) Постройте прямоугольник со сторонами 2, 3 и 5 см.
б) Больший угол треугольника равен 50°. Найдите остальные углы.
в) Две стороны треугольника перпендикулярны третьей. Определите вид
треугольника.
г) Внешний угол при основании равнобедренного треугольника равен 75°. Найдите
углы треугольника.
д) Диагональ ромба в два раза больше его стороны. Найдите углы ромба.
2.Создание проблемных ситуаций через использование занимательных заданий. Прием «яркое пятно» - заключается в сообщении классу интригующего материала, но при этом связанного с темой урока. Это может быть использование сказки, легенды, фрагмента из художественной литературы, случая из истории науки, культуры, повседневной жизни и т.д.
Пример №1. Тема: «Линейная функция»(7 класс)
Обычная форма задания:
функция задана формулой 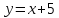 . Найдите значение функции при x = 0, 7, -5, 1.
. Найдите значение функции при x = 0, 7, -5, 1.
Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано 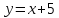 .
.
На доске заготовлена таблица:
Ученик из класса называет какое-нибудь значение х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение у. Затем другой ученик из класса называет другое значение х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу.
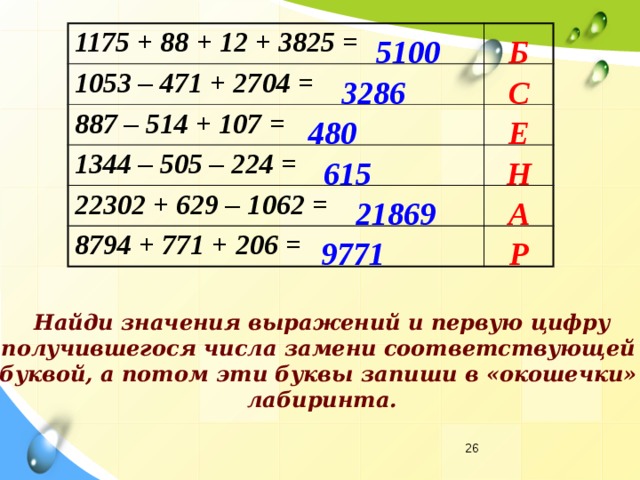
Пример №2. Тема: «Формулы сокращённого умножения»(7 класс)
Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения
( 2y +1)² – 4y² =9
y = 2
597² = (600 – 3)² =6002 -2 • 600 • 3 + 3² = 360000 – 3600 + 9 =356409
Пример №3. Тема «Сумма n-первых членов арифметической прогрессии» (9 класс)
Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствие он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”
Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?
Решение проблемы (1 + 100) • 50 = 5050
Последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической прогрессии.
Главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности.
3. Создание проблемных ситуаций через решение задач, связанных с жизнью. Прием «актуальность» - состоит в обнаружении смысла, значимости предлагаемой темы для самих обучающихся, лично для каждого.
Пример №1. Тема «Периметр прямоугольника»( 5 класс)
Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.
Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).
Пример №2. Тема «Проценты»( 5 класс)
Вы знаете, что в этом году я выиграла в лотерею. Размер выигрыша 10 тыс. руб. Но я получу не все деньги. Вычитают подоходный налог 13%. Я хочу, чтобы вы помогли сосчитать, какую сумму я получу.
Вопрос: «А как же мы вам поможем, если мы не знаем, что такое процент?»
Проблемная ситуация создана. Ребята с удовольствием работают в течении всего урока. В конце урока дорешивают задачу до конца. Я вижу радостные лица ребят. Они справились с проблемой!
4.Создание проблемных ситуаций через выполнение практических заданий.
Пример.№1. Тема «Площадь квадрата»(5 класс)
К уроку вам было дано задание из газеты склеить 1 м². Вы сделали это? Молодцы. Давайте посмотрим, сколько человек поместится на нём. Выясняем, что 4 человека. Как вы думаете, возможно ли на квадратной площадке со стороной 30 км. поместить всё население мира ?( 6,5 млрд.)
Проблемная ситуация: нужно найти площадь площадки (площадь квадрата)
Пример №2. Тема «Координатная плоскость»( 6 класс)
На этапе активного и осознанного усвоения нового материала, а также на этапе закрепления применяю практические работы «Животные на плоскости», «Астрономия и координатная плоскость». Ребята строят точки по координатам и рисуют животных и созвездия, затем рассказывают про них. Также выполняют творческие работы, сами предлагают свои рисунки и по ним составляют задания.
Пример № 3.Темы: «Построение треугольника по трем элементам», «Неравенство треугольника».( 7 класс)
Теорему о неравенстве треугольника вводим при изучении темы «Построение треугольника по трем элементам», решая задачу на построение треугольника по трем его сторонам. Предлагаем ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 9см; 5см; 6см;
в) 1см; 2см; 3см; г) 3см; 4см; 10см.
Ребята работают самостоятельно и приходят к тому, что построить треугольник в последних двух примерах не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи, дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему.
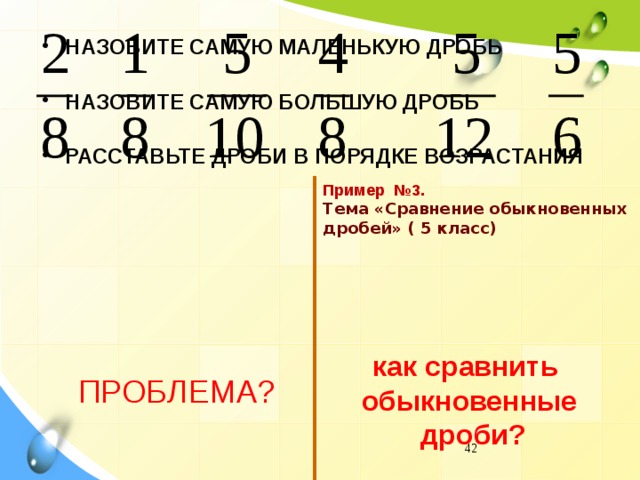
5. Создание проблемных ситуаций через решение задач на внимание и сравнение. Задается вопрос (задание), которое выявляет разные мнения учеников класса, сталкивая их. Какие же мнения верные?
Пример№1. Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе.
Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а, б?
Что общего в данных фигурах, а в чём различие?
Пример №2. Тема: «Площадь трапеции». (8 класс)
При выводе формулы для вычисления площади трапеции учитель предлагает учащимся воспользоваться ранее изученными формулами для вычисления площади прямоугольника, параллелограмма, треугольника, свойствами площадей.
Ребята предлагают различные способы:
а) провести диагональ и найти площадь трапеции как сумму площадей двух треугольников;
б) провести две высоты и найти площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников;
в) провести прямую, параллельную боковой стороне трапеции и найти площадь трапеции как сумму площадей параллелограмма и треугольника.
Пример №3. Тема: «Четырехугольники». ( 8 класс)
К моменту изучения темы «Квадрат» учащимся знакомы такие виды четырехугольников как прямоугольник, ромб и их свойства. Прошу учащихся сформулировать определение квадрата. На что они дают два разных определения: «Квадратом называется прямоугольник, у которого все стороны равны» или «Квадратом называется ромб, у которого все углы прямые». Оба определения верные. Обсуждаем почему имеет право быть каждое из них.
6.Создание проблемных ситуаций через противоречие нового материала старому, уже известному. Дается задание, выполнение которого вызывает затруднения при имеющемся уровне знаний и умений. Почему не смогли выполнить задание?
Пример№1. Тема «Формулы сокращённого умножения»( 7 класс)
Вычисляем (2 • 5)²= 2² •5² = 100
(3 • 4)²= 3² • 4² = 9 • 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25
Попробуйте сосчитать по-другому.
( 3 + 4)² =7² = 49
Проблемная ситуация создана. Почему разные результаты?
( 3 +4)² ≠ 3² + 4²
7. Создание проблемных ситуаций через различные способы решения одной задачи.
Пример. Тема «Решение задач»( 7 класс)
На заправке села две цистерны. В начале посевной обе цистерны заполнены. В 1 было 59 т бензина, а во 2 - 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1 цистерны ежедневно расходуется 5т, а из 2 - 2 т.
Решают с помощью уравнения (алгебраический)
59 – 5х = 44 – 2х
А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить.
Проблемная ситуация: какой способ он предложил (арифметический)
8. Создание проблемных ситуаций через выполнение небольших исследовательских заданий.
Пример№1. Тема «Длина окружности»( 6 класс)
Ещё древние греки находили длину окружности по формуле 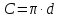 , где d - это диаметр окружности.
, где d - это диаметр окружности.
Вопрос: а что же такое π ?
Работаем в парах, выполняя необходимые измерения.
1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.
| С1 | С2 | С3 | С сред. | 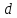 |  |
| | | | | | |
2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу.
3.Найдите значение  , как неизвестного множителя. Можно пользоваться калькулятором.
, как неизвестного множителя. Можно пользоваться калькулятором.
4.Каждой паре занести вычисленное значение  в таблицу на доске.
в таблицу на доске.
Полученные значения
| 1 пара | 2 пара | 3 пара |
| | | |
| среднее арифметическое =( 1 пара +2 пара +3 пара):3 Значение  от 3,1 до 3,2 от 3,1 до 3,2 |
 это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.
это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.
 =3,1415926…
=3,1415926…
Для того, чтобы легче запомнить цифры надо сосчитать количество букв в каждом слове высказывания: «Это я знаю и помню прекрасно» или «Нужно только постараться и запомнить всё как есть: три, четырнадцать, пятнадцать, девяносто два и шесть!»
В дальнейшей работе мы будем использовать значение  =3,14
=3,14
Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь принесли желаемый результат. Проблема решена.
Имея успех в небольших исследованиях на уроках, некоторые ребята вовлекаются в более серьёзные исследования, требующие много времени. Это уникальная возможность для ученика сделать своё открытие, узнать то, что до него никто не знал. Исследования помогают расширить кругозор ученика, повысить самооценку, самоутвердиться, формировать исследовательскую компетентность.
Рекомендации учителям по созданию проблемных ситуаций на уроке.
1.Подводить к противоречию с уже известным и предлагать самим находить способ разрешения.
2. Побуждать делать сравнения, обобщения, выводы.
3. Создавать ситуации включения, используя задания, связанные с их жизненным опытом.
4. Использовать задачи с заведомо допущенными ошибками.
5. Предлагать практические исследовательские задания.
6. Отыскивать различные способы решения одной и той же задачи.
7. Излагать различные точки зрения на один и тот же вопрос.
8.Учить составлять задачи по статистическим данным своего населённого пункта.
Итак, сегодня я познакомила вас с технологией проблемного диалога. Чтобы создать его я применяю различные приёмы, в частности, создание проблемной ситуации.
Преимущества технологии проблемного диалога
Проблемный диалог является мощным источником мотивации познавательной деятельности учащихся.
Проблемный диалог реализуется на любой ступени обучения.
Проблемный диалог дает учителю широкие возможности выбора методов, форм и средств обучения.
В работу включается практически весь класс, что гарантирует усвоение нового материала большинством учеников.
Обеспечивает более качественное усвоение знаний, приучает учащихся мыслить, развивает их интеллектуальные способности и активность.
Вывод:
Сегодня я попыталась показать вам, что использование технологии проблемного диалога, в частности, создание проблемных ситуаций на уроках математики не только формирует ту систему математических знаний, умений и навыков, которая предусмотрена программой, но и самым естественным образом развивает у школьников познавательную и творческую активность. Ситуация затруднения школьника в решении задач приводит к пониманию учеником недостаточности имеющихся у него знаний, что в свою очередь вызывает интерес к познанию и установку на приобретение новых. Всякий раз при разрешении проблемной ситуации я с удовольствием наблюдаю, как ребята не только усваивают новое для себя, но и переживают этот процесс как «открытие» ещё чего-то неизвестного: кто сдержанно (старшеклассники), а кто с нетерпением и восторгом (шестиклассники), торопясь, чтобы его не опередили в «открытии», и обижаясь иногда на себя, если не сумел быть первым, а иногда на меня «почему выбрала другого, а не меня». А мне на каждом уроке приходится думать о том, как ободрить его, заставить поверить в свои силы, снова увидеть горящие глаза. Именно это заставляет меня искать что-то новое, всегда быть в поиске.
Выбор за тобой
«Это невозможно!» - сказала Причина.
«Это безрассудство!» - заметил Опыт.
«Это бесполезно!» - отрезала Гордость.
«Попробуй…» - шепнула Мечта.
Литература
1.Мельникова Е.Л. Проблемный урок, или как открывать знания с учениками: Пособие для учителя. - М., 2002.
2.Мельникова Е.Л. Технология проблемного диалога: методы, формы, средства обучения // Образовательные технологии. Сборник материалов. М., Баласс, 2008.
3. Кульневич С.В. Современный урок. Часть II Проблемные уроки. – Ростов на Дону:
Учитель,2006
8
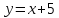 . Найдите значение функции при x = 0, 7, -5, 1.
. Найдите значение функции при x = 0, 7, -5, 1.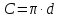 , где
, где 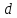





















 100." width="640"
100." width="640"



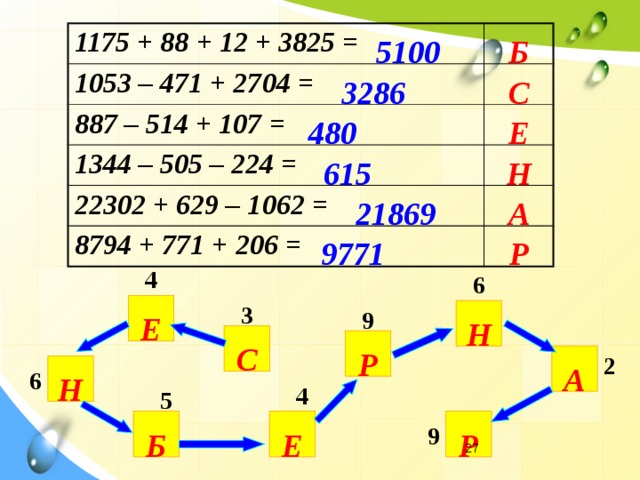













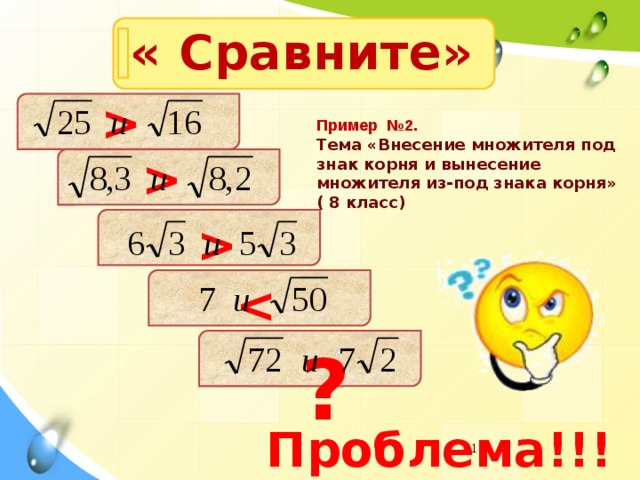 Пример №2. Тема «Внесение множителя под знак корня и вынесение множителя из-под знака корня» ( 8 класс) ? Проблема!!!" width="640"
Пример №2. Тема «Внесение множителя под знак корня и вынесение множителя из-под знака корня» ( 8 класс) ? Проблема!!!" width="640"