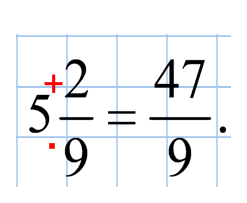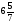В настоящее время образование детей с ограниченными возможностями здоровья — одна из актуальных проблем современного образования. Большинство обучающихся имеет проблемы с запоминанием, поэтому требовать от них выучить определения и формулы зачастую бессмысленно. Акцент при работе с данной категорией детей следует делать не на заучивание, а на развитие умений поиска нужной информации, использования справочных материалов, памяток, схем и т.д.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Памятки по математике для 5 класса(коррекция)
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Памятки по математике для 5 класса(коррекция)»
Полезное для учителя
Распродажа видеоуроков!
1580 руб.
2640 руб.
1280 руб.
2130 руб.
1360 руб.
2260 руб.
1600 руб.
2660 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
600 руб.
3000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
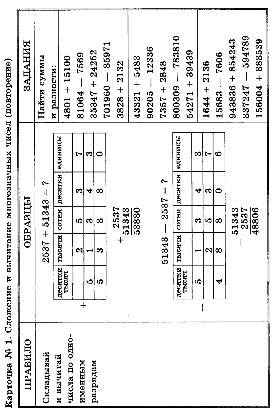


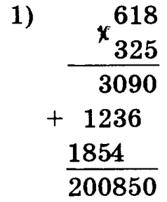
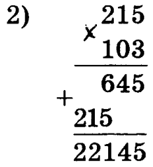

 2) Чтобы число умножить на разность двух чисел, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
2) Чтобы число умножить на разность двух чисел, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.  Например:
Например:  1) 12 ∙ 8 = (10 + 2) ∙ 8 = 10 ∙ 8 + 2 ∙ 8 = 80 + 16 = 96.
1) 12 ∙ 8 = (10 + 2) ∙ 8 = 10 ∙ 8 + 2 ∙ 8 = 80 + 16 = 96.
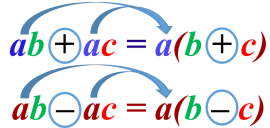




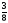 .
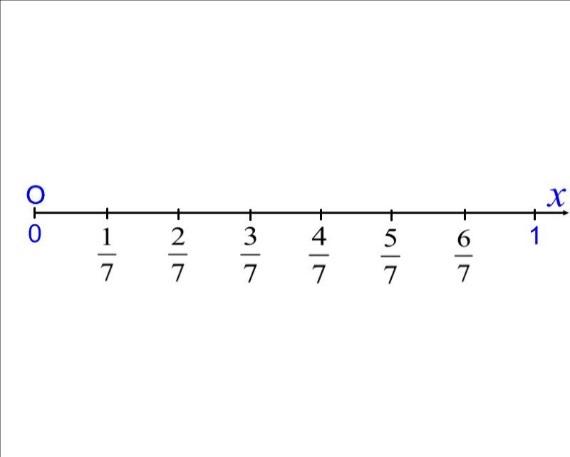
.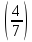 . Единичный отрезок разделить на 7 равных частей, от нуля отсчитать 4 части, отметить точку А.
. Единичный отрезок разделить на 7 равных частей, от нуля отсчитать 4 части, отметить точку А.
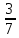 от 28 кг. Решение: 28 : 7 ∙ 3 = 4 ∙ 3 = 12(кг) Ответ: 12 кг
от 28 кг. Решение: 28 : 7 ∙ 3 = 4 ∙ 3 = 12(кг) Ответ: 12 кг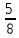 которого составляют 15 км.
которого составляют 15 км.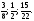
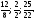
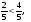 так как 2
так как 2 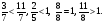
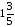 читают так: «Одна целая три пятых».
читают так: «Одна целая три пятых».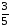 - его дробной частью.
- его дробной частью.