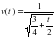Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Проверочная работа "Правила вычисления производных"
Данная работа проверяет навыки вычисления первообразных функций. Данный вид контроля можно использовать на любом этапе урока. Количество вариантов позволяет охватить разнообразными заданиями учащихся класса, что актуально для сельской школы. Уровень заданий "от простого к сложному". Все задания разработаны на основе программы по алгебре и началам анализа 11 класса.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Проверочная работа "Правила вычисления производных" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1650 руб.
2350 руб.
1850 руб.
2640 руб.
1680 руб.
2400 руб.
1650 руб.
2350 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
500 руб.
2500 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
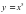 4) у= 3sin x 5) y= cos 10x 6)
4) у= 3sin x 5) y= cos 10x 6) 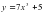
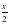 F(-2)=3
F(-2)=3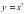 4) у=
4) у= 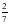 cos x 5) y= sin 17x 6)
cos x 5) y= sin 17x 6) 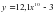
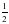 x²-x+1, f(x)=x-1
x²-x+1, f(x)=x-1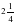 2) у=22х 3)
2) у=22х 3)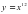 4) у=
4) у= 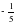 sin x 5) y= cos 0,2x 6)
sin x 5) y= cos 0,2x 6) 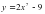
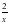 , f(x)= 3 cos x -
, f(x)= 3 cos x - 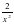
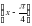 F
F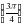 =2
=2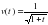
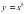 4) у=
4) у= 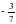 cos x 5) y= sin
cos x 5) y= sin 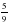 x 6) y=3,2x³-6
x 6) y=3,2x³-6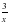 , f(x)=
, f(x)=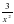 - 2 sin x
- 2 sin x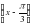 F
F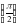 =1
=1