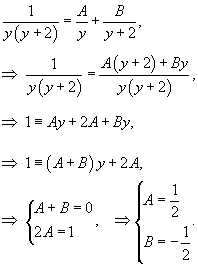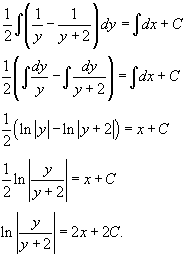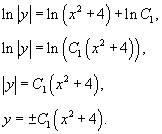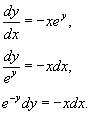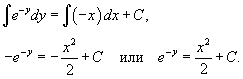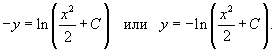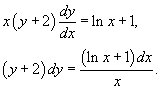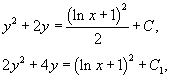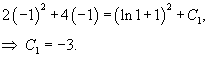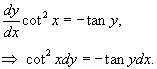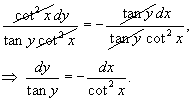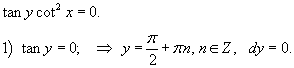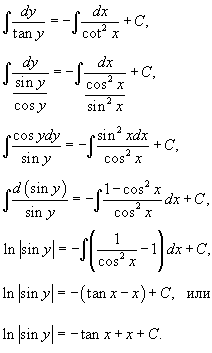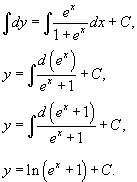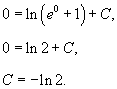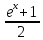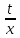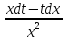ПрактическАЯ РАБОТА№ 17
Тема: Решение дифференциальных уравнений первого порядка с разделяющимися переменными
Цели:
- изучить понятие дифференциального уравнения
- рассмотреть дифференциальные уравнения первого порядка с разделяющимися переменными
- научиться решать дифференциальные уравнения первого порядка с разделяющимися переменными
Оснащение занятия: конспект лекций.
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 20
- Записать в тетрадь разобранные примеры на решение дифференциальных уравнений первого порядка с разделяющимися переменными
Лекция 20.
Дифференциальные уравнения с разделяющимися переменными
| Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y: где p(x) и h(y) − непрерывные функции. в правую часть и разделим уравнение на h(y): Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения. Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение: где C − постоянная интегрирования. описывающее общее решение уравнения с разделяющимися переменными. |