ГККП «РУБЕЖИНСКИЙ КОЛЛЕДЖ»
Рассмотрено на заседании МК ЕМЦ
«__4__» сентября 2014г
Протокол № 1
«УТВЕРЖДАЮ»
Заместитель директора по
учебной работе
«_____» _________ 2014г
_________ _____________
подпись ФИО
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ «МАТЕМАТИКА»
КОД И ПРОФИЛЬ ОБРАЗОВАНИЯ
№1500000 «Сельское хозяйство, ветеринария и экология»
СПЕЦИАЛЬНОСТЬ
№1504000«Фермерское хозяйство»
КВАЛИФИКАЦИИ
№1504062 «Тракторист-машинист сельскохозяйственного производства»
№1504082«Водитель автомобиля»
№1504042«Повар»
НА БАЗЕ ОСНОВНОГО СРЕДНЕГО ОБРАЗОВАНИЯ
СРОК ОБУЧЕНИЯ - 2 года 10 месяцев
ОБЩЕОБРАЗОВАТЕЛЬНЫЙ ЦИКЛ
ДЛЯ ОБУЧАЮЩИХСЯ ОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Составитель: Калинина В.Н., преподаватель математики Рубежинского колледжа
Рубежка, 2014 год
Учебно-методический комплекс по УД Математика составлен в соответствии с Государственным общеобязательным стандартом среднего образования (начального, основного среднего, общего среднего образования), Государственным общеобязательным стандартом технического и профессионального образования, утвержденными Постановлением Правительства Республики Казахстан №1080 от23 августа 2012 года.
Учебно-методический комплекс по дисциплине Математика входит в Общеобразовательный цикл и является частью основной профессиональной образовательной программы Рубежинского колледжа
Учебно-методический комплекс по дисциплине Математика адресован студентам очной формы обучения.
УМКД включает рабочую программу, вопросы для самоконтроля, перечень точек рубежного контроля, а также вопросы и задания по промежуточной аттестации (при наличии).
РАБОЧАЯ ПРОГРАММА
НАИМЕНОВАНИЕ ПРЕДМЕТА: «МАТЕМАТИКА»
КОД И ПРОФИЛЬ ОБРАЗОВАНИЯ
№1500000 «Сельское хозяйство, ветеринария и экология»
СПЕЦИАЛЬНОСТЬ
№1504000«Фермерское хозяйство»
КВАЛИФИКАЦИИ
№1504062 «Тракторист-машинист сельскохозяйственного производства»
№1504082«Водитель автомобиля»
№1504042«Повар»
НА БАЗЕ ОСНОВНОГО СРЕДНЕГО ОБРАЗОВАНИЯ
КОЛИЧЕСТВО ЧАСОВ - 144
СРОК ОБУЧЕНИЯ - 2 года 10 месяцев
Пояснительная записка
Рабочая программа разработана в соответствии с Государственным общеобязательным стандартом среднего образования (начального, основного среднего, общего среднего образования), Государственным общеобязательным стандартом технического и профессионального образования, утвержденными Постановлением Правительства Республики Казахстан №1080 от23 августа 2012 года, Приказом и.о. Министра образования и науки Республики Казахстан от 28 апреля 2014 года №127 «О внесении изменения и дополнений в приказ и.о. Министра образования и науки РК от 27 сентября 2013 года №400 «Об утверждении перечня учебников, учебно-методических комплексов, пособий и другой дополнительной литературы, в том числе на электронных носителях, разрешенных к использованию в организациях образования», на основании учебной программы, утвержденной Приказом Министра образования и науки Республиеи Казахстан № 115 от 3 апреля 2013 года.
Учебный предмет «математика» входит в состав общеобразовательных дисциплин ГОСО РК.
Программа рассчитана на 144 часа, в том числе контрольных работ - 13, включая итоговую контрольную работу. Вся программа изучается на первом курсе ( первый и второй семестры).
Завершением изучения дисциплины является экзамен.
Математическое образование-это испытанное столетиями средство интеллектуального развития в условиях массового обучения.
Цель обучения: освоение учащимися базисных основ математики, овладение ими математическим языком; развитие интереса к математическому творчеству, математической интуиции и математических способностей; воспитание самоопределяющейся личности и ее ценностного отношения к различным видам трудовой деятельности.
Задачи обучения:
обеспечение качественного усвоения базисных основ математики, направленного на развитие интеллектуальных качеств личности;
формирование представлений о математике как форме описания и методе познания действительности, роли математической модели в научном познании реальных процессов;
развитие представлений о математике как части общечеловеческой культуры, о значимости математики в истории цивилизации и современном обществе; расширение общего кругозора обучающихся представлением о вкладе ученых на различных этапах развития математической науки; расширение представлений учащихся о сферах применения математики;
усвоение новых подходов к решению задач по математике, овладение математическими знаниями, нужными для изучения смежных дисциплин на современном уровне; применения математических знаний в повседневной жизни; развитие умений использовать математические знания в практической деятельности;
формирование качеств мышления, необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем; интеллектуальное развитие учащихся; развитие логического мышления; потенциальных творческих способностей каждого учащегося; интереса к предмету;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения; развитие навыков самостоятельной работы, самооценки при выполнении индивидуальных заданий и работе в группе; предоставление учащимся возможности самостоятельного конструирования задач по данной теме, их решения, подготовке презентаций к занятиям; развитие умения ориентироваться в потоке поступающей информации
В результате освоения дисциплины студенты должны уметь:
выполнять арифметические действия, сочетая устные и письменные приёмы, применяя вычислительные устройства; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчётах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя их графики;
вычислять производные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа;
решать рациональные, показательные и логарифмические уравнения и неравенства;
составлять уравнения по условию задачи;
находить приближённые решения уравнений и неравенств, используя графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчёта числа исходов;
распознавать на чертежах и моделях пространственные формы, соотносить трёхмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела;
выполнять чертежи по условиям задач;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
должны знать:
аксиомы стереометрии;
теоремы, выражающие признаки геометрических тел;
определения, свойства алгебраических функций и геометрических тел;
формулы геометрии, алгебры и начала анализа.
Обязательный минимум содержания предмета
Функция, ее свойства и график (12 ч.)
Функция. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функции: возрастание и убывание, чётность и нёчетность, периодичность, промежутки знакопостоянства. Точки экстремума и экстремумы функции. Неубывающая функция. Невозрастающая функция. Обратная функция. Простейшие преобразования графиков функций. Исследование функции и построение её графика
Аксиомы стереометрии. Параллельность прямых и плоскостей (11 ч.)
Основные понятия и аксиомы стереометрии, следствия из аксиом;точки, прямые и плоскости в пространстве;понятие о принадлежности точек и прямых плоскостям; взаимное расположение двух прямых в пространстве: пересекающиеся, параллельные и скрещивающиеся прямые; свойства параллельных прямых в пространстве;признак скрещивающихся прямых;взаимное расположение прямой и плоскости: пересекающиеся и параллельные прямая и плоскость; признак параллельности прямой и плоскости;взаимное расположение двух плоскостей: пересекающиеся и параллельные плоскости;признак параллельности плоскостей, свойства параллельных плоскостей; параллельное проектирование, его свойства
Перпендикулярность прямых и плоскостей (11ч)
перпендикулярность прямых;перпендикулярность прямой и плоскости, признак перпендикулярности прямой и плоскости;свойства перпендикулярных прямой и плоскости; перпендикуляр и наклонная к плоскости, проекция наклонной на плоскость;теорема о трех перпендикулярах;расстояние от точки до плоскости, расстояние между параллельными прямыми и плоскостями, расстояние между скрещивающимися прямыми;угол между прямой и плоскостью, двугранный угол, угол между двумя плоскостями;задачи практического содержания на взаимные расположения прямых и плоскостей.
Тригонометрические функции (12ч.)
Свойства и графики тригонометрических функций. Арксинус, арккосинус, арктангенс, арккотангенс. Преобразования выражений, содержащих арксинус, арккосинус, арктангенс, арккотангенс. Обратные тригонометрические функции;
Простейшие тригонометрические уравнения вида sinх = а, cosх = а, tgх = а, ctgх = а и их решения. Способы решения тригонометрических уравнений (Тригонометрические уравнения, приводимые к алгебраическим уравнениям относительно одной тригонометрической функции. Тригонометрические уравнения, решаемые путем преобразования тригонометрическими формулами. Тригонометрические уравнения, решаемые способом понижения степени уравнения. Однородные тригонометрические уравнения.). Системы тригонометрических уравнений и их решение. Тригонометрическое неравенство. Решение прсотейших тригонометрических неравенств и их систем
Производная (12 ч.)
Предел функции в точке. Производная. Правила нахождения производных. Дифференцирование. Производная степенной функции. Физический и геометрический смысл производной. Касательная к графику функции. Уравнение касательной к графику функции.Сложная функция. Производная сложной функции. Производная тригонометрических функций. Приближённые вычисления
Применение производной к исследованию функций (9 ч.)
Признаки монотонности (возрастания и убывания) функции. Критические точки. Достаточные условия существования экстремума. Исследование функции с помощью производной и построение её графика. Наибольшее и наименьшее значения функции на промежутке
Векторы в пространстве (9 ч.)
прямоугольная система координат в пространстве, координаты середины отрезка, расстояние между двумя точками; векторы в пространстве;разложение вектора по трем некомпланарным, координаты вектора в пространстве, действия над векторами в координатах;скалярное произведение векторов в координатах, свойства скалярного произведения векторов; применение векторов к решению задач.
Комбинаторика и бином Ньютона (3 ч.)
Основные понятия и формулы комбинаторики (перестановки, размещения, сочетания). Бином Ньютона
Первообразная и интеграл (12ч.)
Первообразная функции. Основное свойство первообразной. Правила нахождения первообразных. Криволинейная трапеция. Площадь криволинейной трапеции. Определённый интеграл. Формула Ньютона-Лейбница. Интегрирование. Применение определённого интеграла к решению геометрических и физических задач;
Многогранники. Площади поверхностей и объемы многогранников(14 ч.)
понятие о многограннике, призма, ее элементы; прямая и правильная призмы, параллелепипед: прямой, прямоугольный, куб; свойства параллелепипеда, площадь поверхности призмы; пирамида и ее элементы; правильная пирамида, усеченная пирамида; развертка пирамиды; площадь поверхности пирамиды и усеченной пирамиды;правильные многогранники; объем прямоугольного параллелепипеда, объем призмы, объем пирамиды; задачи практического содержания на нахождение площадей поверхностей и объемов пространственных тел.
Степени и корни (10 ч.)
Корень n-ой степени и его свойства. Арифметический корень n-ой степени. Степень с рациональным показателем и её свойства. Иррациональные уравнения. Решение иррациональных уравнений и их систем. Степенная функция, её свойства и графики. Дифференцирование и интегрирование степенной функции с действительным показателем
Показательная и логарифмическая функции (12ч.)
Показательная функция, ее свойства и график. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Десятичный логарифм. Натуральный логарифм. Логарифмическая функция, ее свойства и график. Дифференцирование показательной и логарифмической функций. Показательные уравнения. Решение показательных уравнений и их систем. Логарифмические уравнения. Решение логарифмических уравнений и их систем. Показательные неравенства. Решение показательных неравенстви их систем. Логарифмические неравенства. Решение логарифмических неравенств и их систем
Тела вращения (11 ч.)
прямой круговой цилиндр, его элементы;сечения цилиндра плоскостью;
развертка цилиндра;площадь поверхности цилиндра; прямой круговой конус, его элементы;сечения конуса плоскостью; развертка конуса;площадь поверхности конуса; усеченный конус и площадь его поверхности;сфера и шар, сечение шара и сферы плоскостью;касательная плоскость к сфере, ее свойства;шаровой сектор и шаровой сегмент; площадь поверхности шара и его частей; объемы цилиндра и конуса;объем шара и его частей;задачи назадачи практического содержания на нахождение объемов пространственных тел.
Уравнения и неравенства (2 ч.)
Уравнения и неравенства, содержащие переменную под знаком модуля. Уравнения и неравенства с параметрами.
Вероятность (2 ч.)
Сложение и умножение вероятностей. Случайная величина.
Формы контроля
текущий: самостоятельная работа, проверочная работа, математический диктант, тест, опрос;
тематический: зачет, контрольная работа.
Формы промежуточной и итоговой аттестации:
Промежуточная аттестация проводится в форме математических диктантов, контрольных и самостоятельных работ.
Виды самостоятельных работ
Индивидуальное решение задач по темам.
Изображение пространственных фигур на плоскости.
Составление таблиц.
Построение графиков по заданным параметрам.
Написание развернутых ответов на вопросы, сообщений, рефератов.
Решение уравнений, неравенств.
Форма контроля самостоятельной работы:
Проверка выполнения индивидуальных заданий.
Защита рефератов.
Выполнение тестовых заданий.
Проверка рабочих тетрадей.
КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УД
Тематический контроль
Контрольные работы
Входящая контрольная работа
Контрольная работа №1 Функция, ее свойства и график
Контрольная работа №2 Аксиомы стереометрии. Параллельность
прямых и плоскостей
Контрольная работа №3 Перпендикулярность прямых и плоскостей
Контрольная работа №4 Тригонометрические функции
Контрольная работа №5 Производная
Контрольная работа №6 Применение производной к исследованию функций
Контрольная работа №7 Векторы в пространстве
Контрольная работа №8 Первообразная и интеграл
Контрольная работа №9 Многогранники, площадь поверхности и объем
многогранника
Контрольная работа №10 Степени и корни
Контрольная работа №11 Показательная и логарифмическая функции
Контрольная работа №12 Тела вращения
Контрольная работа №13 Итоговая контрольная работа
КОНТРОЛЬНАЯ РАБОТА
«ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК»
Вариант 1
1. Найдите область определения функции:
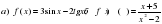 .
.
2. Определите, является ли функция 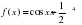 четной или нечетной?
четной или нечетной?
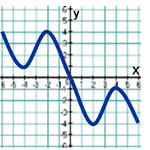
3. Проведите по общей схеме исследование функции, заданной графиком, изображенным на рисунке.
4. Исследуйте функцию и постройте ее график.
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ:
«СТЕПЕНИ И КОРНИ»
Вариант 1
1. Вычислите: 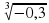 ·
· 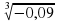
2. Упростите выражение: 1,4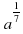 : 2
: 2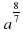
3. Вычислите 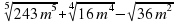 при m = –
при m = – 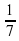 .
.
4. Решите уравнение 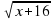 = х – 4 .
= х – 4 .
5. Решите уравнение 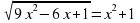
КОНТРОЛЬНАЯ РАБОТА
ПО ТЕМЕ « ТЕЛА ВРАЩЕНИЯ»
Вариант 1
1. Объем цилиндра равен 63π см3, а площадь осевого сечения 18 см2. Найдите радиус основания цилиндра.
2. Объем конуса равен 9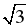 π см3. Найдите высоту конуса, если его осевое сечение – равносторонний треугольник.
π см3. Найдите высоту конуса, если его осевое сечение – равносторонний треугольник.
3. Вычислите диаметр шара, если его объем V = 36π.
4. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
«ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ»
Вариант 1
1.Какая функция является возрастающей?
у = 0,2Х; 2) у = 3х; 3) у = 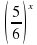 ; 4) у = 2 – х
; 4) у = 2 – х
2. Решите уравнение.
(1/5)3-2х=125
3. Вычислите.
2log36-log312
4. Решите уравнение.
lg(x + 1,5) = – lgx
5. Решите неравенство
log1/3(4+х)≤-2
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
«МНОГОГРАННИКИ. ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ МНОГОГРАННИКА»
Вариант II.
1.Боковое ребро правильной четырёхугольной призмы равно 6см, а диагональ боковой грани – 10см. Найдите боковую поверхность и объём призмы.
2.В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
3.Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4. 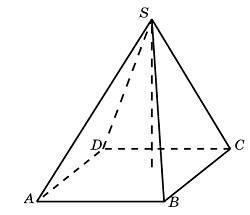
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
«ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ»
Вариант I
1.Докажите, что функция F является первообразной для функции f на множестве R
F(x) = x4 – 3, f(x) = 4x3.
2. Для функции f(x) = 3х2-4х +2 найдите первообразную , график которой проходит через точку М(3;8)
3. Вычислите интеграл:
а) 
4.Вычислите площадь фигуры, ограниченной линиями у = 1 – х2; у = 0; х = -1.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
Вариант 1
Найдите значение выражения  log
log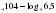
Решите уравнение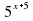 = 0,04.
= 0,04.
Высота конуса равна 30, а длина образующей - 34. Найдите диаметр основания конуса
Сравните числа: а). 2,7π и 2,73;
Найдите производную функции у = 0,25 х4 + cos (0,5х)
Вычислите определенный интеграл 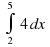
Найдите наибольшее и наименьшее значения функции f(x) = х3 – 3х2 + 4 на промежутке [0;4].
Функция задана графиком. Найдите область значений этой функции.
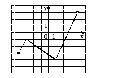
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
1 вариант
На каком расстоянии от плоскости (Оху) находится точка А(2; -3; -5)
На каком расстоянии от начала координат находится точка А(-3; 4; 0)
Найти координаты середины отрезка, если концы его имеют координаты А(5; 3; 2) и В(3; -1; -4)
Найти длину вектора 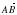 , если А(5; 3; 2), В(3; -1; -4)
, если А(5; 3; 2), В(3; -1; -4)
2 вариант
На каком расстоянии от плоскости (Охz) находится точка B(-3; 2; -4)
На каком расстоянии от начала координат находится точка B(3; 0; -4)
Найти координаты середины отрезка, если концы его имеют координаты
А(-3; 2; -4) и В(1; -4; 2)
Найти длину вектора 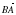 , если А(5; 3; 2), В(3; -1; -4)
, если А(5; 3; 2), В(3; -1; -4)
ЗАЧЕТЫ ПО ГЕОМЕТРИИ
Карточка 2
Расскажите о связи между координатами векторов и координатами точек.
Выведите формулы, выражающие координаты середины отрезка через координаты его концов.
Вычислите угол между прямыми АВ и СD, если А(1; 1; 0), В(3; -1; 0), С(4; -1; 2), D(0; 1; 0).
Карточка 3
Сформулируйте определение скалярного произведения двух векторов. Сформулируйте условие перпендикулярности двух ненулевых векторов с помощью скалярного произведения.
Выведите формулу для вычисления длины вектора по его координатам.
Даны точки А(0; 4; 0); В(2; 0; 0); С(4; 0; 4); D(2; 4; 4). Докажите, что ABCD-ромб.
ТЕМАТИЧЕСКИЙ ТЕСТ ПО ТЕМЕ «СТЕПЕННАЯ ФУНКЦИЯ, ЕЁ СВОЙСТВА И ГРАФИК».
1 вариант.
1. Известно, что f(х)= . Вычислите f(
. Вычислите f(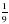 ).
).
А. 243 В. 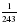 С.
С. 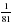 D. 81 Е.
D. 81 Е.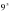
2. Известно, что f(х)=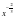 . Найдите f(
. Найдите f(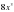 ).
).
А. 2х В. 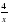 С. 4х D.
С. 4х D. 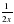 Е.
Е.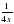
3. Исследуйте степенную функцию у=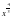 на чётность.
на чётность.
А. ни чётная, ни нечётная В. Чётная С. нечётная
4. Исследуйте на возрастание и убывание функцию у = 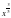 .
.
А. неубывает и не возрастает В. только возрастает
С. убывает на промежутке (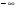 ;0), возрастает на промежутке (0;
;0), возрастает на промежутке (0;  ).
).
D. только убывает Е. возрастает на промежутке (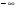 ;0), убывает на промежутке (0;
;0), убывает на промежутке (0;  ).
).
5. Найдите промежутки знакопостоянства функции у=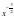 .
.
А. yxВ. y0, x0 С. y0, x0; yxD.y0, x0; y0, xЕ.y0, x
6.Найдите промежутки возрастания и убывания функции у=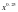 .
.
А. возрастает на промежутке (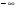 ;0], убывает на промежутке (0;
;0], убывает на промежутке (0;  ).
).
В. убывает на промежутке (0;  ). С. возрастает на промежутке (
). С. возрастает на промежутке (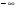 ;0), убывает на промежутке (0;
;0), убывает на промежутке (0;  ). D. возрастает на промежутке (0;
). D. возрастает на промежутке (0; )
)
Е. возрастает на промежутке [0; )
)
7. Найдите наибольшее и наименьшее значения функции у= на отрезке [4;16].
на отрезке [4;16].
А. 16, 4 В. 32, 8 С. 64, 4 D. 64, 8 Е. 16, 8
8. Найдите область определения функции у=
А. все R числа
В. [0;  )
)
С. (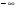 ; 0]
; 0]
D. (
Е. (0;  )
)
9. Определите, сколько точек пересечения имеют графики функции у= и у=2.
и у=2.
А. одна
В. две
С. нет точек пересечения
D. четыре
Е. три
10. Определите множество значений функции у= .
.
А. 
В. 
С. (-
D. 
Е.
ТЕСТ ПО ТЕМЕ: «СВОЙСТВА ФУНКЦИЙ»
Вариант №2
1. Найдите область определения функции, график которой изображен на рисунке.
 2.
2. Функция задана графиком. Найдите область значений этой функции.
 3.
3. Найдите промежутки возрастания функции

, заданной графиком на полуинтервале

.

4. Укажите наименьшее значение функции  , заданной на отрезке
, заданной на отрезке  .
.
| 1) | ‑ 3 |
| 2) | ‑ 4 |
| 3) | ‑ 5 |
| 4) | 4 |
 5.
5. Укажите промежуток убывания функции

, заданной графиком на интервале

.

ТЕСТ ПО ТЕМЕ: « ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ВЫРАЖЕНИЯ»
Вариант №1
1. Укажите, какое из чисел не входит в область определения выражения  .
.
| 1) | 
| 2) | 2 | 3) | 0 | 4) | 4 |
2. Укажите, какое из данных чисел входит в область определения выражения  ?
?
3. Укажите выражение, в область определения которого входит число 3.
4. При каких значениях переменной x имеет смысл выражение  ?
?
5. При каких значениях переменной x выражение  не имеет смысла?
не имеет смысла?
ИТОГОВЫЙ КОНТРОЛЬ ПО УД
Экзамен проходит в форме тестирования. В каждом варианте содержится 25 вопросов, 5 вариантов ответа, из которых только один верный.
Пример тестового задания
ЭКЗАМЕНАЦИОННОЕ ЗАДАНИЕ В ТЕСТОВОЙ ФОРМЕ.
Вариант- 1
1. Найдите площадь прямоугольника, если его длина равна 9,6 см, а ширина равна 3,8 см.
A) 116,544 см2 B) 55,68 см2 C) 128,64 см2 D) 36,48 см2 E) 50,92 см2
2. Упростите выражение: (5а + b)(b – 5a)
A) 25a2 – b2 B) a2 + b2 C) 5a2 + b2 D) b2 – 25a2 E) 10a2 – b2
3. Определите радиус сферы, если ее площадь равна 100π см2.
A) 
 ; B)
; B)  ; C).
; C).  . D)
. D) . E) 25см
. E) 25см
4. Разложить на множители: 2х2 - 18
A) 2(х2 + 9) B) 2(х – 3)(х + 3) C) 2(х – 9)(x + 9) D) (2x – 3)(2x + 3) E) (2x – 9)(2x + 9)
5. Периметр ромба равен 15 см. Найдите сторону ромба
A) 3,25 см B) 3,5 см C) 7,5 см D) 3,75 см E) 5 см
6. Решите систему уравнений: 
A) (2; 4); (4; 2)
B) (1; 5); (2; 4) C) (1; 5) D) (3; 3); (1; 5) E) (3; 3); (4; 2)
7. Вычислить: 
А) 1; В) 2; С)  . D) 0 E) 4
. D) 0 E) 4
8. Решите уравнение: 
A) -  B)
B)  C)
C)  D)
D)  E) 0
E) 0
9. f(x)= x7- 4x5 + 2x – 1. Найдите  (x)
(x)
A) x7 – 20x3 + 2 B) 7x6 – 20x4 + 2 C) x7 – 20x4 – 1 D) x7 – 20x + 2 E) 7x6 – 20x5 + 2x – 1
10. Решите уравнение: 
A) 1 B) 2 C) 4 D) 5 E) 6
11. Решите систему уравнений: 
A) (-2; 1), (-1; 2)
B) (2; 1), (-1; -2) ) C) (-1; 3), (1; -1) D) (2; -1), (-1; 1) E) (2; 3), (3; 2)
12. Чему равны стороны прямоугольника, если они относятся как 2:3, а ее площадь 24 см2
A) 4 см, 6 см B) 3 см, 8 см C) 6 см, 9 см D) 8 см, 12 см E) 4 см, 5 см
13. Вычислите 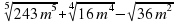 при m = –
при m = – 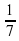 .
.
А). 3; В) 2; C) 1/7 D)  ; E) - 1/7
; E) - 1/7
14. Радиусы оснований усеченного конуса 3 дм и 7 дм, образующая 5 дм. Найдите площадь осевого сечения
A) 80 дм2 B) 120 дм2 C) 30 дм2 D) 60 дм2 E) 100 дм2
15. Вычислите: 
A) 3 B) -18 C) 9 D) 6 E) 0
16. Решите систему уравнений: 
A) (-3; 5), (-5; 8)
B) (2; 7), (-2; -7) C) (-1; 5), (-5, -8)
D) (3; -5), (5; -8) E) (-2; -4), (3; 5)
17. Найдите значение выражения  .
.
A) 3 B) 0 C) 9 D) 6 E) 2
18. . Найдите значение производной функции y = 4x2 – 9 в точке х0= -3.
A) 25 B) 36 C) -24 D) 6 E) 0
19. Вычислите:  , если
, если 
A)  B)
B)  C)
C)  D)
D)  E)
E) 
20. Если две прямые имеют одну общую точку, то они называются
А) параллельными; В) пересекающимися; C) перпендикулярными. D) скрещивающимися
21. Решите систему неравенств: 
A) (0; 4)
B) [0; 4] C) [0; 3) D) [3; 4) E) (3; 4)
22 Определите площадь осевого сечения цилиндра, если оно имеет форму квадрата, а радиус основания цилиндра равен 5 см.
А) 100см2; В) 45см2; C) 150см2 D) 50 см2 E) 25см2
23. Найти область определения функции: 
A) (-1; 1)
B) [1; + ] C) (-
] C) (- ; 1) D) [-1; 1] E) (-
; 1) D) [-1; 1] E) (- ; -1)
; -1) (-1; 1)
(-1; 1) (1;
(1;  )
)
24. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 см и 8 см. Высота призмы 7 см. Найдите площадь поверхности этой призмы
A) 48 см2 B) 264 см2 C) 168 см2 D) 216 см2 E) 192 см2
25. В результате вращения какой фигуры получается конус?
А) прямоугольника; В) треугольника; C) трапеции; D) шара. E) круга
Шкала оценки образовательных достижений
| Процент результативности (правильных ответов) | Оценка уровня подготовки |
| балл (отметка) | вербальный аналог |
| 90 ÷ 100 | 5 | отлично |
| 80 ÷ 89 | 4 | хорошо |
| 70 ÷ 79 | 3 | удовлетворительно |
| менее 70 | 2 | неудовлетворительно |
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Основные источники:
| Основная литература (учебники) | Учебно-методическая литература | Учебные и справочные пособия |
| Алгебра и начала анализа 10 | *Алгебра и начала анализа10 АбылкасымовА, ЕсеноваМ, ЖумагуловаЗ. Методическое руководство Мектеп 2006 | Программы «Математика» *Алгебра и начала анализа10 Сборник задач Мектеп 2006 *Алгебра и начала анализа10 Дидактические материалы Мектеп 2006 |
| Алгебра и начала анализа11 | *Алгебра и начала анализа 11 Абылкасымова А. БекбоевИ., Абдиев А. Методическое руководство Мектеп 2007 | *Алгебра и начала анализа11 Абылкасымова А.,Шойынбеков К., Жумагулова З. Сборник задач Мектеп 2007 *Алгебра и начала анализа11 Абылкасымова А.,Шойынбеков К.,ЖумагуловаЗ. Дидактические материалы Мектеп 2007 |
| Геометрия 10. Гусев В., Кайдасов Ж., Қағазбаева А. 2010 Мектеп | *Геометрия.10 Методическое руководство для учителя Кайдасов Ж., Гусев В., Қағазбаева А.,Ахматуллина М. Мектеп 2010 | *Геометрия 10 Кайдасов Ж., Гусев В.,Есенгазин Е. Сборник задач Мектеп 2010
*Геометрия 10 Кайдасов Ж., Гусев В., Дидактические материалы Мектеп 2010 |
| Геометрия 11 Шыныбеков А. 2011 Атамұра | *Геометрия 11 Методическое руководство Мектеп 2007 | *Геометрия 11 Гусев В., Кайдасов Ж., Е.Есенгазин Сборник задач Мектеп 2007
*Геометрия 11 Гусев В., Кайдасов Ж. Дидактические материалы Мектеп 2007 |
Дополнительные источники:
Интернет-ресурсы:
Предметные Интернет- ресурсы,
www.school-collection.edu.ru
www.ict.edu.ru
http:// www. Pedlib. Ru/- педагогическая библиотека
http:// www.inter-pedagogika/ru - сайт создан для преподавателей, родителей и студентов.
www.mathematics.ru
Цифровые образовательные ресурсы
Консультации по математике на первом курсе
| Тема занятия | Кол-во часов |
| Действия с числовыми выражениями | 1 |
| Действия с дробными выражениями | 1 |
| Формулы сокращенного умножения | 1 |
| Формулы сокращенного умножения | 1 |
| Плоские фигуры и их свойства | 1 |
| Решение задач из планиметрии(треугольники) | 1 |
| Решение задач из планиметрии(четырехугольники) | 1 |
| Линейные уравнения | 1 |
| Квадратные уравнения | 1 |
| Линейные неравенства | 1 |
| Квадратные неравенства | 1 |
| Графический метод решения уравнений | 1 |
| Простейшие преобразования графиков функций | 1 |
| Простейшие тригонометрические уравнения и их решения | 1 |
| Способы решения тригонометрических уравнений и их систем | 1 |
| Правила нахождения производных | 1 |
| Физический и геометрический смыслы производной. Уравнение касательной к графику функции | 1 |
| Производная сложной функции Производная тригонометрических функции | 1 |
| Критические точки и экстремумы функции | 1 |
| Исследование функции с помощью производной и построение графика Наибольшее и наименьшее значения функции | 1 |
| Координаты вектора в пространстве. Действия над векторами в координатах. | 1 |
| Применение векторов к решению задач. | 1 |
| Криволинейная трапеция и ее площадь | 1 |
| Вычисление площадей плоских фигур и объемов тел с помощью определенного интеграла | 1 |
| Иррациональные уравнения | 1 |
| Показательные уравнения Показательные неравенства | 1 |
| Логарифмические уравнения Логарифмические неравенства | 1 |
| Площади боковой и полной поверхностей многогранников | 1 |
| Площади поверхности цилиндра, конуса. | 1 |
| Объемы тел вращения | 1 |
| всего | 30 |
Нормы оценки знаний, умений и навыков
по математике.
Оценка письменных контрольных работ обучающихся по математике
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно
Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
ПЛАН РАБОТЫ
КАБИНЕТА «МАТЕМАТИКА И ФИЗИКА»
Задачи кабинета математики и физики
на ________учебный год
Обеспечение качественного выполнения программы по математике и физике
Организация фронтальной учебной деятельности с использованием мультимедиапроектора и компакт-дисков учебного назначения, а также ресурсов Интернета.
Организация доступа студентов к Интернет- ресурсам по математике и физике.
Обеспечение комфортных условий труда, соблюдение санитарно- гигиенических норм в кабинете.
Поддержание в рабочем состоянии оборудования для лабораторных работ и демонстрационных опытов, имеющихся в кабинете.
Пополнение кабинета современной справочной литературой, раздаточными и дидактическими материалами.
Развитие устойчивого интереса к математике через внеклассные мероприятия и уроки.
Подготовка УМК по математике
Повышение качества знаний по математике и физике.
Организационная работа
| № п/п | Мероприятия | Срок исполнения | Ответственный |
| 1 | Провести учет учебного оборудования, имеющегося в кабинете | Последняя неделя августа | Зав.кабинетом |
| 2 | Провести профилактический осмотр оборудования для лабораторных работ и демонстрационных опытов | 1 неделя сентября | Зав.кабинетом |
| 3 | Составить план работы кабинета | До 10 сентября | Зав.кабинетом |
| 4 | Составить график работы кабинета | 1 неделя сентября | Зав.кабинетом |
| 5 | Составить график работы факультативов, расписание консультаций | До 10 сентября | Зав.кабинетом |
| 6 | Оформить журналы по ТБ. | 1 неделя сентября | Зав.кабинетом |
| 7 | Обновить медикаменты в аптечке | 1 неделя сентября | Зав.кабинетом |
| 8 | Обновить паспорт кабинета. | До 10 сентября | Зав.кабинетом |
| 9 | Приобретение методической литературы | сентябрь | Зав.кабинетом |
| 10 | Инвентаризация оборудования кабинета.
| Октябрь-ноябрь | Зав.кабинетом |
Укрепление материально - технической базы
| № п/п | Мероприятия | Срок исполнения | Ответственный | | 1 | Освоение и использование инновационного оборудования в процессе обучения
| В течение года | Зав. кабинетом | | 2 | Обновление стенда «Изучаем математику» | сентябрь | Зав. кабинетом | | 3 | Приобрести электронное учебное пособие «Анимационные ролики по стереометрии: http://urokimatematiki.ru/stereometriya2.html»
| В течение года | Зав. кабинетом | | 4 | Организовать группу по изготовлению и ремонту: - учебно-методических пособий; - наглядных пособий; - демонстрационных моделей;
| октябрь | Актив кабинета | | 5 | Подготовить заявку на приобретение постоянных стендов для кабинета | ноябрь | Зав. кабинетом | | 6 | Обновить стенд «Основные физические константы» | сентябрь | Зав. кабинетом | | 7 | Подготовить стенд по технике безопасности в кабинете | октябрь | Зав. кабинетом | | 8 | Создание презентаций студентами для последующего использования их на занятиях | В течение года | Актив кабинета | | 9 | Готовить компьютерные программы к использованию на занятиях (тренажеры, тестирующие устройства и т.п.) | В течение года |
Зав. кабинетом | № п/п | Мероприятия | Срок исполнения | Ответственный |
| 1 | Составить перспективно-тематические планы, утвердить их на ЦМК |
До 15. 09 |
Зав. кабинетом |
| 2 | Составить график взаимопосещений. | сентябрь | Зав. кабинетом
|
| 3 | Переутвердить рабочие программы. |
До 15. 09 | Преподаватели математики и физики |
| 4 | Провести входные диагностические работы | 4 неделя сентября | Преподаватели математики и физики |
| 5 | Подготовить УМК по математике | сентябрь | Калинина В.Н. |
| 6 | Составить план участия в Неделе цикловой комиссии. | сентябрь | Преподаватели математики и физики |
| 7 | Подготовка методических разработок открытых уроков | декабрь | Калинина В.Н. Мещанов И.Н. |
| 8 | Утверждение конспектов открытых уроков на заседании цикловой комиссии. | декабрь | Калинина В.Н. Мещанов И.Н. |
| 9 | Добавить варианты в проверочные, контрольные и лабораторные работы | октябрь | Калинина В.Н. Мещанов И.Н. |
| 10 | Завести электронные «папки» для отдельных тем с доп. материалом в соответствии с учебной программой. | В течение года | Зав. кабинетом |
| 11 | Изучать методические материалы по дисциплине в сети Интернет | В течение года | Зав. кабинетом
|
| 12 | Провести систематизацию имеющихся в кабинете методических материалов. | сентябрь | Зав. кабинетом
|
| 13 | Работа с периодикой в библиотеке. | В течение года | Преподаватели математики и физики |
| 14 | Подготовить контролирующие тесты для диагностики уровня знаний студентов | В течение года | Зав. кабинетом
|
| 15 | Создание компьютерных презентаций для проведения уроков | В течение года | Зав. кабинетом
|
| 16 | Использование на занятиях готовых медиаресурсов | В течение года | Преподаватели математики и физики |
| 17 | Участие в Интернет-проектах | сентябрь, октябрь | Преподаватели математики и физики |
| 18 | Анализ методической работы за год. | июнь | Зав. кабинетом
|
| 19 | Разработка заданий для аттестации студентов | 2 семестр | Преподаватели математики и физики |
| 20 | Продолжить работу по усовершенствованию поурочной электронной картотеки.
| В течение года | Преподаватели математики и физики |
| 21 | Готовить материал для публикаций в методических изданиях | февраль | Зав. кабинетом
|
Внеурочная работа
| № п/п | Мероприятия | Срок исполнения | Ответственный |
| 1 | Проведение консультаций и дополнительных занятий по математике, физике |
По графику |
Зав. кабинетом |
| 2 | Работа с сильными студентами
| В течение года | Зав. кабинетом
|
| 3 | Подготовка сообщений, рефератов, докладов; новости достижений науки, новые открытия в мире математики, физики |
В течение года | Преподаватели математики и физики |
| 4 | Оформление учебно-методических и наглядных пособий, стендов, плакатов | В течение года | Преподаватели математики и физики |
| 5 | Работа с учебными изданиями, Интернет-ресурсами | В течение года | Зав. кабинетом |
| 6 | Подготовка авторских публикаций
| В течение года | Зав. кабинетом |
| 7 | Подготовка студентов к предметным олимпиадам, конкурсам, проектам.
| Декабрь- январь | Калинина В.Н. Мещанов И.Н. |
| 8 | Проведение факультативных занятий | По графику | Калинина В.Н. Мещанов И.Н. |
| 9 | Подготовка и проведение Недели естественно- математических дисциплин | март | Калинина В.Н. Мещанов И.Н. |
| 10 | Физико- литературный конкурс «Я познаю науки» | ноябрь | Преподаватели физики и литературы |
| 11 | Оформление и пополнение стенда «Изучаем математику» | В течение года | Зав. кабинетом |
ПЛАН УРОКА
Преподаватель математики Рубежинского колледжа Калинина В.Н.
Тема урока: «Объём призмы»
Задачи урока:
Учебные- обобщить и систематизировать имеющиеся у учащихся сведения о призме и ее объеме, формировать умения применять теоретические знания к решению практических задач;
Развивающие- развивать логическое мышление, интерес к предмету, умение самостоятельно работать;
Воспитательные- воспитание умения проводить оценку и самооценку знаний и умений, воспитание трудолюбия, аккуратности; пропагандировать здоровый образ жизни.
Тип урока: урок комплексного применения знаний
Форма: практикум по решению задач
Оборудование: модели призм, флаконы одеколона или лосьона , коробки из- под сока (в форме призмы), компьютер, проектор, презентация, линейка.
Ожидаемые результаты:
Возрастание интереса к предмету.
Формирование умений применять имеющиеся знания на практике.
Ход урока
Организационно- психологический настрой на урок
Мотивация
Разминка
У учащегося - прямоугольный равнобедренный угольник и прямоугольный угольник с углом 300.
Дается задание:
1. Молча подтвердить мысль:
а) Существует треугольник, в котором есть прямой угол. (Учащийся поднимает один из угольников).
б) Существует треугольник, в котором две стороны перпендикулярны. (Учащийся поднимает один из угольников и пальцем показывает эти стороны).
2. Молча опровергнуть утверждение:
а) Не найдется треугольника, в котором есть острый угол. (Учащийся поднимает угольник с углом 300, но держит его за острый угол).
б) Не найдется треугольника, в котором сумма двух углов равна третьему. (Учащийся поднимает один из двух угольников)
Актуализация знаний учащихся
Тест на повторение теоретического материала по теме (работа в парах, с взаимопроверкой и исправлением неправильных ответов).
Формирование умений и навыков
Решение задач на развитие глазомера
Коробки из-под сока, флаконы различные…- предлагает преподаватель учащимся
Учащиеся называют примерную вместимость предложенных емкостей, затем делают необходимые измерения , вычисления и сравнивают с названной цифрой (групповая работа-3 учащихся )
Учащиеся заполняют таблицу
| Длина
(а) | Ширина
(b) | Высота
(h) |
Sосн.
| Sбок.пов. | V |
|
|
|
|
|
|
|
Решение задач с практическим содержанием
Классное помещение должно быть таким, чтобы на одного учащегося приходилось не менее 6 м³ воздуха. Можно ли в кабинете с параметрами a=8,5 м, b=6 м, c=3,6 м заниматься с 30 учащимися, не нарушая санитарной нормы?
Решение: V= So∙ h =8,5 ∙6 ∙3,6=183,6 (м ³); 183,6:30=6,12 (м³) воздуха приходится на одного учащегося.
Да, в кабинете можно заниматься с 30 учащимся.
Суточное выпадение осадков составило 20 мм. Сколько воды выпало за сутки на треугольную (правильный треугольник) клумбу со стороной 6м?
Решение. Клумба-прямая треугольная призма, где h= 20 мм =0.02 м, V= So∙ h , So=½∙6∙6∙sin 60º =9√3 ≈15,3 (м²). V=15,3∙ 0,02= 0,306≈ 0,3(м³)=300 дм³=300 л.
ответ: За сутки на клумбу выпало 300л осадков
Сколько сена (в кг) вмещает сеновал размерами 6*3*4 м, если тюк сена имеет размеры0,8*0,4*0,5м и массу 20 кг.
Дано: параллелепипеды
а=6м, b=3м, с=4м
а1=0,8м, b2=0,4м, с2=0,5м
m=20кг
Найти: mсена
Решение: Vc= 6∙3∙4=72 м3
Vc= 0,8∙0,4∙0,5=0,16 м3 n=72:0,16=450(тюков) m=450∙20=9000 кг=9т Ответ: m=9т
Какое количество кирпича сможет перевезти машина, имеющая размеры кузова 3,6м*2,3м*1м? Размеры кирпича 25см*12см*8см.
Домашнее задание: подобрать или придумать задачу с практическим содержанием по теме «Призма».
Подведение итогов урока. Преподаватель предлагает закончить предложения:
– «Сегодня на уроке я понял (а), что мне необходимо…»
– «При решении задач с практическим содержанием необходимо…»
– «Самое трудное для меня…»
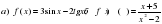 .
.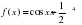 четной или нечетной?
четной или нечетной?
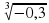 ·
· 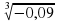
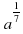 : 2
: 2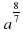
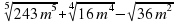 при
при 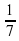 .
.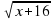 = х – 4 .
= х – 4 .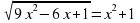
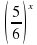 ; 4) у = 2 – х
; 4) у = 2 – х 


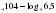
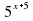 = 0,04.
= 0,04.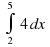
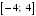

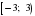
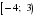

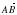 , если А(5; 3; 2), В(3; -1; -4)
, если А(5; 3; 2), В(3; -1; -4)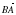 , если А(5; 3; 2), В(3; -1; -4)
, если А(5; 3; 2), В(3; -1; -4) . Вычислите
. Вычислите 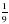 ).
).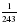 С.
С. 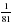
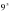
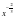 . Найдите
. Найдите 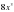 ).
).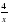 С. 4х
С. 4х 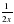 Е.
Е.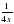
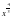 на чётность.
на чётность.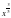 .
.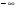 ;0), возрастает на промежутке (0;
;0), возрастает на промежутке (0;  ).
).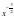 .
.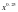 .
.