В школьном курсе математики предлагается очень мало задач на «смеси и сплавы». Эти задачи предлагаются на ЕНТ, вступительных экзаменах в вузы на экономические специальности на факультетах, связанных с легкой промышленностью и народным хозяйством. Задачи на «смеси и сплавы» встречаются на олимпиадах.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Учимся решать задачи на смеси и сплавы
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Учимся решать задачи на смеси и сплавы»
Полезное для учителя
Распродажа видеоуроков!
1440 руб.
2400 руб.
1160 руб.
1940 руб.
1410 руб.
2350 руб.
1430 руб.
2380 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
3560 руб.
17800 руб.
800 руб.
4000 руб.
600 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



 % никеля 40% никеля
% никеля 40% никеля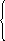 х+у=140,
х+у=140, 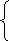
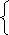 х – у = 200,
х – у = 200,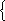 Задача 8. Имеется смесь из двух веществ массой 900 г. После того как выделили
Задача 8. Имеется смесь из двух веществ массой 900 г. После того как выделили 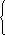 Составляем систему х + у = 118,
Составляем систему х + у = 118, 4x + 14у= 100,
4x + 14у= 100,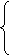 а + 2с = 7 ∙ 0,78,
а + 2с = 7 ∙ 0,78,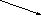
 0 % меди, цинк
0 % меди, цинк х г 70 г
х г 70 г