Мастер-класс на тему:
"Красота привлекает, исследование увлекает"
Цели урока:
Образовательная: показать методические приемы решения нестандартных задач через систему заданий на уроках математики и технологии.
Развивающая: создать условия для формирования рефлексивной, технологической, информационной и коммуникативной компетентностей
Воспитательная: создать условия, способствующие формированию внимательности, ответственности, условия для воспитания коммуникативной культуры, умений выслушивать и уважать мнение других.
Организационный момент.
(Презентация-слайд 1).
Сегодня я постараюсь организовать нашу встречу так, чтобы мы смогли познакомиться с несколькими темами, которые можно использовать, как на уроках, так и на внеурочных занятиях по математике.
Все эти темы я объединила в небольшое путешествие.
Однажды я услышала такую фразу:
«Не бойся учиться тому, что никогда не знал!
Не бойся делать то, что никогда не делал!»
Все мы чему-то учимся, и каждый день делаем что-то новое. Возможно то, чем я предлагаю вам сегодня заняться и будет для вас этим новым. А возможно кто-то уже это знает и умеет. И что-то добавит свое.
(Презентация-слайд 2).
Тема моего занятия «Красота привлекает, исследование увлекает»
Эпиграф: «Предмет математики настолько серьезен, что нельзя упускать случая, сделать его немного занимательным».
Блез Паскаль.
Человек по-разному открывает для себя красоту. Сегодня мы совершим путешествие в красоту математики и технологии.
(Презентация-слайд3).
Я предлагаю вам выбрать карточку определенного цвета.
(Раздаются карточки с примерами, на которых определенное количество с ответом «3», другие с ответом – «6» и остальные с ответом «5»)
Начнем с устного счета. На обороте карточки написаны примеры. Выполните эти не сложные вычисления.
Те, у кого ответ «5» занимают места за первым столом, те, у кого ответ «6» за вторым столом, и те, у кого ответ «3» сидят в зрительном зале.
(Презентация-слайд 3).
Обратите внимание на экран.
Перед вами выражение: 28k + 30n + 31m = ?
(Уравнение, красочно оформленное, вывешивается сверху, в центре доски, к концу урока будет найдено его решение).
К концу занятия мы постараемся найти с вами хотя бы одно решение для этого задания.
(Презентация-слайд 4).
А пока начинаем наше путешествие в математику и технологию! Наш маршрут проложен через следующие остановки.
Остановка: Развиваем гибкость ума через решение задач.
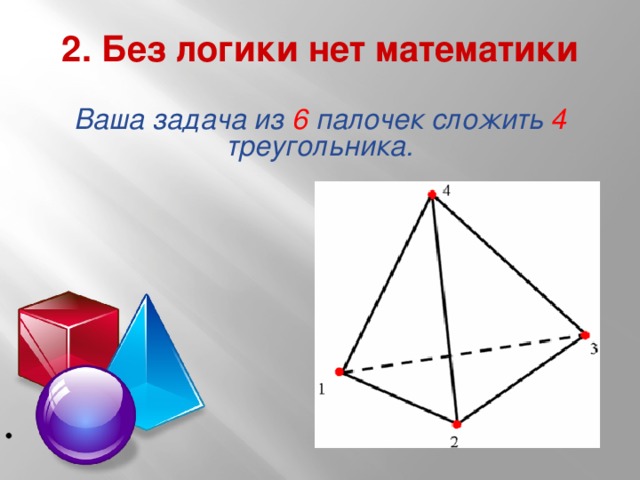
Остановка: Без логики нет математики.
Остановка: В технологию тропинки одолеем без запинки.
Остановка: И фокусы покажем, и секрет расскажем!
(Презентация-слайд5).
1 остановка. Развиваем гибкость ума через решение задач.
Задача для группы «5»:
Известно, что бумеранг можно бросить так, что он вернется обратно. А можно как-то ухитриться и бросить теннисный мяч так, чтобы он вернулся обратно? (дать теннисный шарик и дать возможность продемонстрировать)
Ответ: мяч нужно бросить вверх и он вернется обратно. [1]
(Презентация-слайд6).
2 остановка. Без логики нет математики.
Задача для группы «6»:
Вам необходимо из 6 палочек равной длины сложить 4 одинаковых треугольника.
Ответ: надо сложить пирамиду.
3 остановка. В технологию тропинки одолеем без запинки.
(Презентация-слайд 7). Вопрос: без чего невозможно сделать табуретку, даже если есть все-все инструменты и все-все деревяшки, гвозди, клей?
Ответ: невозможно сделать табуретку без умения.
Мы решили две нестандартные математические задачи, где нужно было просто думать и мало что делать руками, а сейчас рассмотрим задания, в которых требуется умение мастерить, конструировать и думать.
Из обычного листа бумаги можно изготовить самые удивительные фигуры и геометрические тела.
(Презентация-слайд 8-9).
Искусство складывания бумаги называют оригами.
(Презентация-слайд 10).
Давно в древние века в Японии, когда люди приходили в храм, то в качестве подношений приносили фигурки, сложенные из бумаги – оригами. Недаром “ори” означает складывать, а “ками” - “бумага”. Постепенно оригами выходит за пределы храмов. Умение складывать становится одним из признаков хорошего образования.
В 19 веке оригами постепенно распространяется по всему миру. Среди любителей оригами можно отметить Леонардо да Винчи и Льюиса Кэролла. Известно, что Л.Н.Толстой был знаком с оригами.
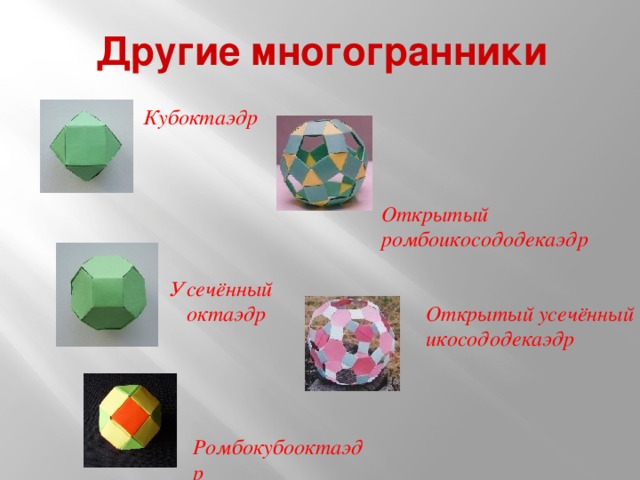
Вот примеры геометрических тел из оригами, изображения которых вы видите на экране.
(Презентация-слайд 11).
Задание для группы «5» изготовить хотя бы одно геометрическое тело из бумаги.
(Презентация-слайд 12-13).
4 остановка. И фокусы покажем, и секрет расскажем!
(Презентация-слайд 14).
Задание для группы «6» будет немного таинственным. Они проведут опыты с волшебными бумажными лентами.
У обеих групп на столе технологические карты для работы.
А пока наши группы выполняют задания, мы с группой «3» выполним красивое задание «Цветок из бесконечности»
(из шаров для моделирования сделать цветы)
(Презентация-слайд15).
Цветок собрали. Мы молодцы! А теперь слово участникам, которые работали за столами «5» и «6».
По готовности каждая группа демонстрирует свои произведения искусств.
(Презентация-слайд16).
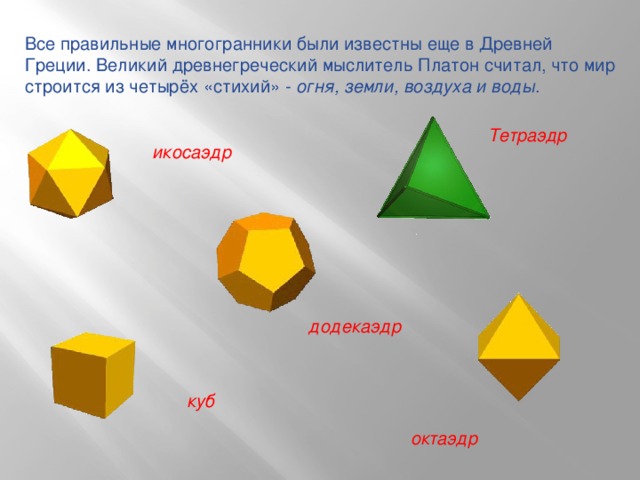
Отчет группы «5»
Все правильные многогранники были известны еще в Древней Греции. Великий древнегреческий мыслитель Платон считал, что мир строится из четырёх “стихий” – огня, земли, воздуха и воды. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. Пятый многогранник – додекаэдр символизировал весь мир и считался главнейшим.
Отчет группы «6»
Лента Мебиуса представляет собой ленту, у которой конец соединили с началом, получив что-то вроде тора. Но, соединяя, повернули один из концов на 180 градусов относительно другого.
Интересность ленты заключается уже в том, что в отличие от обыкновенного листа бумаги она имеет только одну поверхность, а не две. То есть, если начать закрашивать лист бумаги, не переходя через грань, то закрасится только одна сторона. Если проделать то же самое с лентой Мебиуса, лента закрасится с обеих сторон.
Загадки продолжаются и, когда мы начинаем разрезать ленту Мебиуса. Что будет, если разрезать обычный лист бумаги? Конечно же, два обычных листа бумаги. А что случится, если разрезать по центральной линии ленту Мебиуса? Бумага не распадется на две части, а останется целой. Причем имеет сходный вид с лентой Мебиуса. Только перекручена будет дважды, и на сей раз имеет две поверхности, а не одну как в начале.
Как Вы думаете, что станет с этой фигурой, если ее снова разрезать? Может быть, снова выйдет одна целая, но перекрученная полоска бумаги? Нет. На этот раз получатся уже два сцепленных кольца.
Вот такие интересные метаморфозы таит в себе лента Мебиуса. Вы можете показать друзьям эти явления, выдавая их за фокусы, тогда как на самом деле Вы просто продемонстрируете им математические законы.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности. Однако по имеющимся историческим сведениям символ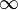 
стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
(Презентация-слайд18).
Итог занятия.
Вернемся к заданию, которое вызывало у нас вопросы в начале занятия.
28k + 30n + 31m = 365
Кто увидел? Кто догадался? Кто решил?
“Смотреть – не значит видеть!”
Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365.
(Презентация-слайд19).
А кто может ответить, чем еще замечательно число 365?
Оно равно сумме квадратов чисел 10, 11, 12 и 13 и 14.
А еще? Оказывается, в библии 365 раз повторяется фраза: « Не бойся!» по разу на каждый день.
(Презентация-слайд19).
И мне хотелось бы вам сказать: «Не бойтесь учить и учитесь сами, и делайте то, что еще не сделали!»
Спасибо за внимание!
5
.
.
