Муниципальное автономное общеобразовательное учреждение
города Набережные Челны
«Средняя общеобразовательная школа №38»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ПО ГЕОМЕТРИИ (8 КЛАСС)
ПО ТЕМЕ «ЧЕТЫРЕХУГОЛЬНИКИ»
ЕРЁМЕНКО НАТАЛЬИ АЛЕКСАНДРОВНЫ,
УЧИТЕЛЯ МАТЕМАТИКИ
МЕТОДИКА ПРОВЕДЕНИЯ БУКВЕННОГО ДИКТАНТА ПО ГЕОМЕТРИИ (8 КЛАСС)
ПО ТЕМЕ « ЧЕТЫРЕХУГОЛЬНИКИ»
Данный вид диктанта проводится по окончании изучения главы на повторительно-обобщающем уроке, когда необходимо проверить и оценить ЗУН уч-ся по изученным темам.
Каждое определение, признак или теорема зашифровано буквой алфавита (например, А – четырёхугольник, Р - теорема Фалеса, И – признак параллелограмма) и записаны на доске (или представлены на слайде).
Учитель диктует учащимся вопросы поочерёдно по вариантам (определение, теорему или признак), уч-ся ищут ответ среди зашифрованных ответов.
Задания составляются в двух вариантах:
Нечётные вопросы для первого варианта, чётные - для второго.
Вопросы диктанта.
№ вопр.
Формулировка вопроса
1.
Фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
2.
Отрезки, соединяющие вершины.
3.
Вершины, являющиеся концами одной из сторон четырёхугольника.
4.
Вершины, не являющиеся соседними.
5.
Отрезки, соединяющие противолежащие вершины четырёхугольника.
6.
Стороны, исходящие из одной вершины.
7.
Стороны, не имеющие общего конца.
8.
Четырёхугольник, у которого противолежащие стороны параллельны.
9.
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот
четырёхугольник – параллелограмм.
10.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
11.
У параллелограмма противолежащие стороны равны.
12.
Параллелограмм, у которого все углы прямые.
13.
У параллелограмма противолежащие углы равны.
14.
Параллелограмм, у которого все стороны равны.
15.
Параллелограмм, у которого все стороны равны.
16.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной из сторон равные
отрезки, то они отсекают равные отрезки и на другой его стороне.
17.
Отрезок, соединяющий середины двух сторон треугольника.
18.
Четырёхугольник, у которого только две противолежащие стороны параллельны.
19.
Трапеция, у которой боковые стороны равны.
20.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные
отрезки.
Учащиеся записывают в качестве ответа только букву.
А
Четырёхугольник
Б
Стороны
В
Соседние вершины
Г
Противолежащие вершины
Д
Диагонали
Е
Соседние стороны
Ж
Противолежащие стороны
З
Параллелограмм
И
Признак параллелограмма
К
Свойство диагоналей параллелограмма
Л
Свойство противолежащих сторон параллелограмма
М
Прямоугольник
Н
Свойство противолежащих углов параллелограмма
О
Ромб
П
Квадрат
Р
Теорема Фалеса
С
Средняя линия треугольника
Т
Трапеция
У
Равнобокая трапеция
Ф
Обобщённая теорема Фалеса
ОТВЕТЫ .
Вариант 1
Вариант 2
1.
А
2.
Б
3.
В
4
Г
5.
Д
6.
Е
7.
Ж
8.
З
9.
И
10.
К
11.
Л
12.
М
13.
Н
14.
О
15.
П
16.
Р
17.
С
18.
Т
19.
У
20.
Ф
Такая методика проверки ЗУН уч-ся позволяет:
- учитывать индивидуальные особенности уч-ся;
-проверять качество усвоения теоретического материала;
- сэкономить время на опрос уч-ся;
- оперативно проверить и оценить выполнение работы.
Просмотр содержимого документа
«Методическая разработка»
Муниципальное автономное общеобразовательное учреждение
города Набережные Челны
«Средняя общеобразовательная школа №38»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ПО ГЕОМЕТРИИ (8 КЛАСС)
ПО ТЕМЕ «ЧЕТЫРЕХУГОЛЬНИКИ»
ЕРЁМЕНКО НАТАЛЬИ АЛЕКСАНДРОВНЫ,
УЧИТЕЛЯ МАТЕМАТИКИ
МЕТОДИКА ПРОВЕДЕНИЯ БУКВЕННОГО ДИКТАНТА ПО ГЕОМЕТРИИ (8 КЛАСС)
ПО ТЕМЕ « ЧЕТЫРЕХУГОЛЬНИКИ»
Данный вид диктанта проводится по окончании изучения главы на повторительно-обобщающем уроке, когда необходимо проверить и оценить ЗУН уч-ся по изученным темам.
Каждое определение, признак или теорема зашифровано буквой алфавита (например, А – четырёхугольник, Р - теорема Фалеса, И – признак параллелограмма) и записаны на доске (или представлены на слайде).
Учитель диктует учащимся вопросы поочерёдно по вариантам (определение, теорему или признак), уч-ся ищут ответ среди зашифрованных ответов.
Задания составляются в двух вариантах:
Нечётные вопросы для первого варианта, чётные - для второго.
Вопросы диктанта.
| № вопр. | Формулировка вопроса |
| 1. | Фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. |
| 2. | Отрезки, соединяющие вершины. |
| 3. | Вершины, являющиеся концами одной из сторон четырёхугольника. |
| 4. | Вершины, не являющиеся соседними. |
| 5. | Отрезки, соединяющие противолежащие вершины четырёхугольника. |
| 6. | Стороны, исходящие из одной вершины. |
| 7. | Стороны, не имеющие общего конца. |
| 8. | Четырёхугольник, у которого противолежащие стороны параллельны. |
| 9. | Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. |
| 10. | Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. |
| 11. | У параллелограмма противолежащие стороны равны. |
| 12. | Параллелограмм, у которого все углы прямые. |
| 13. | У параллелограмма противолежащие углы равны. |
| 14. | Параллелограмм, у которого все стороны равны. |
| 15. | Параллелограмм, у которого все стороны равны. |
| 16. | Если параллельные прямые, пересекающие стороны угла, отсекают на одной из сторон равные отрезки, то они отсекают равные отрезки и на другой его стороне. |
| 17. | Отрезок, соединяющий середины двух сторон треугольника. |
| 18. | Четырёхугольник, у которого только две противолежащие стороны параллельны. |
| 19. | Трапеция, у которой боковые стороны равны. |
| 20. | Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. |
Учащиеся записывают в качестве ответа только букву.
| А | Четырёхугольник |
| Б | Стороны |
| В | Соседние вершины |
| Г | Противолежащие вершины |
| Д | Диагонали |
| Е | Соседние стороны |
| Ж | Противолежащие стороны |
| З | Параллелограмм |
| И | Признак параллелограмма |
| К | Свойство диагоналей параллелограмма |
| Л | Свойство противолежащих сторон параллелограмма |
| М | Прямоугольник |
| Н | Свойство противолежащих углов параллелограмма |
| О | Ромб |
| П | Квадрат |
| Р | Теорема Фалеса |
| С | Средняя линия треугольника |
| Т | Трапеция |
| У | Равнобокая трапеция |
| Ф | Обобщённая теорема Фалеса |
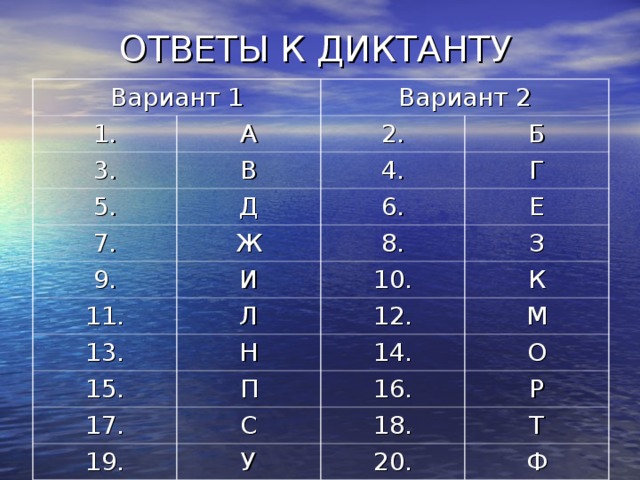
ОТВЕТЫ .
| Вариант 1 | Вариант 2 |
| 1. | А | 2. | Б |
| 3. | В | 4 | Г |
| 5. | Д | 6. | Е |
| 7. | Ж | 8. | З |
| 9. | И | 10. | К |
| 11. | Л | 12. | М |
| 13. | Н | 14. | О |
| 15. | П | 16. | Р |
| 17. | С | 18. | Т |
| 19. | У | 20. | Ф |
Такая методика проверки ЗУН уч-ся позволяет:
- учитывать индивидуальные особенности уч-ся;
-проверять качество усвоения теоретического материала;
- сэкономить время на опрос уч-ся;
- оперативно проверить и оценить выполнение работы.
Просмотр содержимого презентации
«Презентация к разработке Ерёменко Н.А.»

Методика проведения буквенного геометрического диктанта
Геометрия 8 класс

Вопросы диктанта

№
Формулировка вопроса
1.
Фигура, которая состоит из четырех точек и 4 последовательно соединяющих их отрезков.
2.
Отрезки, соединяющие вершины.
3.
Вершины, являющиеся концами одной из сторон четырехугольника.
4.
Вершины, не являющиеся соседними.
5.
Отрезки, соединяющие противолежащие вершины четырехугольника.
6.
Стороны, исходящие из одной вершины.
7.
Стороны, не имеющие общего конца.
8.
Четырехугольник, у которого противолежащие стороны параллельны.

9.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник-параллелограмм.
10
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
11
У параллелограмма противолежащие стороны равны.
12
Параллелограмм, у которого все углы прямые.
13
У параллелограмма противолежащие углы равны.
14
Параллелограмм, у которого все стороны равны.
15
Параллелограмм, у которого все стороны равны.

16
Если параллельные прямые, пересекающие стороны угла, отсекают на одной из сторон равные отрезки, то они отсекают равные отрезки и на другой его стороне.
17
Отрезок, соединяющий середины двух сторон треугольника.
18
4-угольник, у которого только 2 противолежащие стороны параллельны.
19
Трапеция, у которой боковые стороны равны.
20
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Уч-ся записывают ответ буквой
А
Четырехугольник
Б
Стороны
В
Соседние вершины
Г
Противолежащие вершины
Д
Диагонали
Е
Соседние стороны
Ж
Противолежащие стороны

З
Параллелограмм
И
Признак параллелограмма
К
Свойство диагоналей параллелограмма
Л
Свойство противолежащие сторон параллелограмма
М
Прямоугольник
Н
Свойство противолежащих углов параллелограмма
О
Ромб

П
Квадрат
Р
Теорема Фалеса
С
Средняя линия треугольника
Т
Трапеция
У
Равнобокая трапеция
Ф
Обобщённая теорема Фалеса
ОТВЕТЫ К ДИКТАНТУ
Вариант 1
1.
Вариант 2
А
3.
2.
В
5.
7.
Б
4.
Д
9.
Ж
Г
6.
Е
8.
И
11.
10.
З
Л
13.
К
15.
12.
Н
17.
П
14.
М
О
16.
С
19.
Р
18.
У
Т
20.
Ф





























