Вариант №1
А1:Выберите правильный ответ решения неравенства: (х-2)(х+0,3)≥0
1.(-∞;-0,3]U[2;∞)
2. [-0,3;2]
3.(-0,3;2)
4.[2;∞)
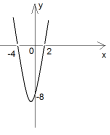
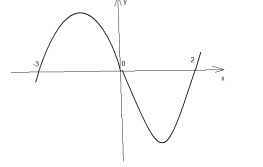
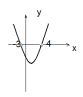
А2: На рисунке изображен график функции у=х²-2х-15. Используя график, решите неравенство: х²-2х-15>0.
1.[-3;5]
2.(-3; 5)
3.(-∞;-3)U(5;∞)
4.(5;∞)
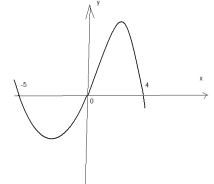
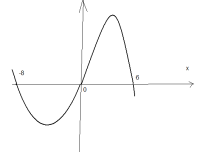
А3: На рисунке изображен график функции у=f(x), решите неравенство f(x) <0
1.(-8;0)U(0;6)
2.(- ∞-;8)U(6;∞)
3.(-8;0)U(0;6)
4.(-8;0)U(6;∞)
А4: При каких значениях х имеет смысл выражение
1.(-2;2)
2.(-∞;-2)
3.(2;∞)
4.(-∞;-2)U(2;∞)
В1: Найдите целые решения неравенства: ≥ 1
С1:Решите неравенство, используя метод интервалов: (х²-2х-3)2 ≤ (х²-3х)2
Вариант №2
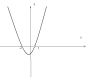
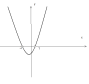
А1: На рисунке показано решение неравенства -х²+4 * 0.
Какой знак следует вписать вместо *?
1.≤
2.<
3.≥
4.>
А2: Для каждого неравенства: А. х²+49<0; Б. х²-49<0; В. х²-49>0,
укажите множество его решений
1) Нет решений; 2) (-∞; -7)U(7;∞); 3) (-7;7).
1. 1;2;3
2. 1;3;2
3. 3;1;2
4. 2;3;1
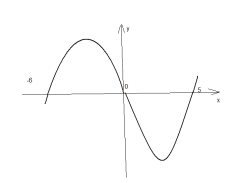
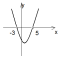
А3: На рисунке изображен график функции у=f(x), решите неравенство f(x) > 0
1.(-∞;-5)U(0;4)
2.(-∞;-5)U(4;∞)
3.(-5;0)U(4;∞)
4.(-5;0)U(0;∞)
А4:Решите неравенство: х²-9>0
1.(-∞; -3)U(3; ∞)
2.(-3;3)
3.(-∞; -3)
4.(3;∞)
В1: Ширина прямоугольника на 4 см меньше длины. Какую ширину должен иметь прямоугольник, чтобы его площадь была больше 21 см² ?
С1:Решите неравенство: х² - (3x-1)/2 > х-1
Вариант №3
А1: Для каждого неравенства: А. х²+16<0; Б. х²-16<0; В. х²-16>0,
укажите множество его решений
1) Нет решений; 2) (-∞; -4)U(4;∞); 3) (-4;4).
1. 1;2;3
2. 1;3;2
3. 3;1;2
4. 2;3;1
А2: Используя график функции у= х² + х -2 , решите неравенство х²+х-2<0.
1.( -2;1)
2.(-∞; -2)U(1;∞)
3.[-2;1]
4.(2;∞)
А3: На рисунке изображен график функции у=f(x), решите неравенство f(x) > 0
1.(-∞; -6)U(5;∞)
2.(-6;0)U(5;∞)
3.(-6;0)U(0;5)
4.(-∞;-6)U(5;∞)
А4: Найдите значения х, при которых трехчлен 4х²-4х+1 принимает положительные значения.
1.0,5
2.(-∞;0,5)
3.(0,5;∞)
4.(-∞; 0,5)U(0,5;∞)
В1:Найдите целые решения неравенства: 3x/(x-1)≤ 2
С1: Решите неравенство: (x-4)(x-3)(3x-7-х²-)/(х²-+x-2)>0
Вариант №4
А1: Используя график функции у= х² + х -2 , решите неравенство х²+х-2>0.
1.(-∞; -2)U(1;∞)
2.( -2;1)
3.[-2;1]
4.(2;∞)
A2: Выберите правильный ответ решения неравенства: (х-5)(х+1)≤0.
1.(-1;5)
2.[-1;5]
3.(-∞;-1)U(5;∞)
4.(-∞;-1]U[5;∞)
А3:На рисунке изображен график функции у=f(x), решите неравенство f(x) <0
1.(-3;0)U(0;2)
2.(-∞;-3)U(2;∞)
3.(-∞; -3)U(0;2)
4.(-3;0)U(2; ∞)
А4: Верно ли, что при любом значении а верно неравенство 1>2а-5а²
1.нет
2.да
3.только при а=0,5
4.Если аЄ (0;∞)
В1: Длина прямоугольника на 3 см больше ширины. Какую длину должен иметь прямоугольник, чтобы его площадь была меньше 28 см²?
С1: При каких значениях с множеством решений неравенства х²-8х+с<0 является промежуток (3; 5)?
Вариант №5
А1: Выберите правильный ответ решения неравенства: (х-3)(х+4)≤0.
1.(-4;3)
2.[-4;3]
3.(-∞;-4)U(3;∞)
4.(-∞;-4]U[3;∞)
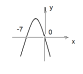
А2: На рисунке изображен график функции у=-х²- 7х. Используя график, решите неравенство -7х>х².
1.(-∞;0)
2.(-∞;-7)U(0;∞)
3.(-7;∞)
4.(-∞;-7)U(0;∞) (-7;0)
А3: При каких значениях х принимает отрицательные значения функция:
у=(х-1,1)(х²+7)?
1.(-7; 1,1)
2.(-∞; -7)
3.(-∞; 1,1)
4.(-∞; -7)U(1,1;∞)
А4:Решите неравенство: - 2х²+5х-2<0
1.(-1; 3,5)
2.(-∞;-1)
3.(-∞; -1)U(3,5;∞)
4.(3,5; ∞)
В1: Найдите область определения функции: у=1/SQL(30-x-х²)
С1:Решить неравенство:1/(2-x) + 5/(2+x) < 1
Вариант №6
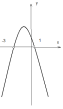
А1: На рисунке изображен график функции у=-х²-2х+3. Используя график , решите неравенство: -х²-2х+3>0.
1.[-3;1]
2.(-∞;-3)U(1;∞)
3.(-3;1)
4.(1;∞)
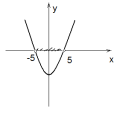
А2: На рисунке показано решение неравенства х² * 25.
Какой знак следует вписать вместо *?
1.≤
2.>
3.≥
4.<
А3: При каких значениях х данный трехчлен х²-19+18 не меньше нуля?
1.(1;18)
2.(-∞; 1]U[18; ∞)
3.[1;18]
4.(-∞; 1)U(18; ∞)
А4:Решите неравенство: х2-11х+30≤ 0
1.(-∞; 6)
2.(5;6)
3.(6;+∞)
4.(-∞; 5)U( 6; ∞)
В1: Используя разложение на множители, определите, при каких значениях х данное выражение принимает неотрицательные значения: 16х-х5
С1: Найдите решения неравенства 0,6х² ≤ 0,5-1,3х, принадлежащие промежутку [0,25;1]
Вариант №7
А1:Выберите правильный ответ решения неравенства: (х-4)(х+0,7)≥0
1.(-∞;-0,7]U[4;∞)
2.[-0,3;2]
3.(-0,3;2)
4.[2;∞)
А2: На рисунке изображен график функции у=х² -х-12. Используя график, решите неравенство: х² -х-12<0.
1.(-∞;-3)U(4;∞)
2.[-3;4]
3.(-3;4)
4.(4;∞)
А3: При каких значениях х данный трехчлен х²-17х+16 неотрицателен?
1.(-∞;1)U(16; ∞)
2.(1;16)
3.[1;16]
4. (-∞;1]U[16; ∞)
А4: Верно ли, что при любом значении а верно неравенство 6а<а2+10
1.Только при а=0,6
2.нет
3.да
4.Если аЄ(0;∞)
В1: Используя разложение на множители, определите, при каких значениях х данное выражение принимает неотрицательные значения: х-81х5
С1: Планер должен пролететь 60 км по направлению ветра и вернуться обратно не позже, чем через 5 часов. При какой скорости ветра это возможно, если собственная скорость планера 25 км/ч?
Вариант №8
A1: На рисунке изображен график функции у=х²+2х-3. Используя график, решите неравенство: х²+2х-3<0.
1.(-∞;-3)U(1;∞)
2.[-3;1]
3.(-3;1)
4.(1;∞)
А2: Выберите правильный ответ решения неравенства: (х-1,2)(х+3)≥0
1.(-∞;-3]U[1,2;∞)
2. [-3;1,2]
3.(-3;1,2)
4.[1,2;∞)
А3: При каких значениях х принимает положительные значения функция:
у=(х2+2)(х-1,5)
1.(1,5; ∞)
2.(-2; 1,5)
3.(-∞; -2)
4.(-∞; -2)U(1,5; ∞)
А4: Найдите значения х, при которых трехчлен -16х²+8х-1 принимает отрицательные значения.
1.(-∞;0,25)U(0,25;∞)
2. 0,25
3.(-∞;0,25)
4.(0,25;∞)
В1: Найдите область определения функции: у=SQL(x+20-х²)
С1: Найдите область определения функции: у=SQL(-х²+2IxI+3)
 При каких значениях х имеет смысл выражение
При каких значениях х имеет смысл выражение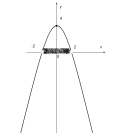
 0.
0.