
Теория вероятностей и комбинаторные правила для решения задачи ЕГЭ В10. Новые прототипы (2013)

Классическое определение вероятности
Стохастическим называют опыт, если заранее нельзя предугадать его результаты. Результаты (исходы) такого опыта называются событиями .
Пример: выбрасывается игральный кубик (опыт); выпадает двойка (событие).
Событие, которое обязательно произойдет в результате испытания, называется достоверным , а которое не может произойти, - невозможным .
Пример: В мешке лежат три картофелины.
Опыт – изъятие овоща из мешка.
Достоверное событие – изъятие картофелины.
Невозможное событие – изъятие кабачка.

Классическое определение вероятности
Несовместимыми (несовместными) называют события, если наступление одного из них исключает наступление других.
Пример: 1) В результате одного выбрасывания выпадает орел (событие А) или решка (событие В).
События А и В - несовместны.
2) В результате двух выбрасываний выпадает
орел (событие А) или решка (событие В).
События А и В - совместны. Выпадение орла в первый раз
не исключает выпадение решки во второй

Классическое определение вероятности
Полной группой событий называется множество всех событий рассматриваемого опыта, одно из которых обязательно произойдет, а любые два других несовместны.
Полной группой событий называется множество всех событий рассматриваемого опыта, одно из которых обязательно произойдет, а любые два других несовместны.
События образующие полную группу называют элементарными.
Пример: 1) Опыт – один раз выбрасывается монета.
Элементарные события: выпадение орла
и выпадение решки образуют полную группу.

Классическое определение вероятности
Вероятностью случайного события А называется отношение числа элементарных событий m, которые благоприятствуют этому событию, к общему числу всех элементарных событий, входящих в данную группу n .
Сумма вероятностей всех событий, входящих в полную группу равна 1.
Пример: Опыт – один раз выбрасывается монета.
А – выпал орел Р(А)=0,5
Полная группа.
В – выпала решка Р(В)=0,5

Классическое определение вероятности
Два события, образующие полную группу называются противоположными.
А – за одно выбрасывание выпала решка
В – за одно выбрасывание выпал орел
А и В – противоположные события

Классическое определение вероятности
Равновозможными называют события, если в результате опыта ни одно из них не имеет большую возможность появления, чем другие.
Примеры: 1) Опыт - выбрасывается монета.
Выпадение орла и выпадение решки –
равновозможные события.
2) В урне лежат три шара. Два белых и синий.
Опыт – извлечение шара.
События – извлекли синий шар и извлекли
белый шар - неравновозможны.
Появление белого шара имеет больше шансов.
Вероятности равновозможных событий равны.

Классическое определение вероятности
Произведением событий А и В называется событие АВ , которое наступает тогда и только тогда, когда наступают оба события: А и В .
Вероятность произведения совместных событий равна произведению вероятностей этих событий.
Пример: Найти вероятность того, что в результате двух выбрасываний игральной кости выпадет шестерка.
Событие А (первый раз выпала шестерка Р(А)=1/6) и событие В (второй раз выпала шестерка Р(В)=1/6) - совместны.

Классическое определение вероятности
Суммой событий А и В называется событие А + В , которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Вероятность наступления суммы несовместных событий равна сумме вероятностей этих событий.
Пример: Найти вероятность того, что в результате одного выбрасывания игральной кости выпадет шестерка или двойка.
Событие А (выпала шестерка Р(А)=1/6) и событие В (выпала двойка Р(В)=1/6) - несовместны.

Классическое определение вероятности
Вероятность наступления суммы совместных событий равна сумме вероятностей наступления этих событий минус вероятность их произведения.
Пример: Найти вероятность того, что в результате двух выбрасываний игральной кости выпадет один раз шестерка или один раз двойка.
Событие А (выпала шестерка Р(А)=1/12) и событие В (выпала двойка Р(В)=1/12) - совместны.

Задачи открытого банка.
Классическое определение вероятности.

№ 319170 В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение:
Благоприятных событий – 4.
Всего событий – 16.
Р=4/16=0,25
Ответ:0,25

№ 320190 На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение:
Неудобных мест 12+18=30
Событие А – досталось удобное место.
Всего событий – 300 (равно количеству мест)
Р(А)=30/300=0,1
Ответ:0,1

№ 320181 В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение:
Возможные комбинации пар из 5 человек (1,2,3,4,5)
34
45
23
12
13
24
35
14
25
15
Всего - 10
У каждого 4 шанса
Ответ:0,4
Р=4/10=0,4

№ 320205 Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Решение:
А- «Статор» начинает игру
В- начинает игру другая команда
«Статор» играет с тремя командами
Всего - 8
АВВ
ААА
ВВВ
Возможные
комбинации:
ААВ
Благоприятное - 1
ВВА
АВА
ВАВ
ВАА
Ответ:0,125

№ 320212 На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Решение:
Благоприятное событие А – паук пришел к выходу D. Одно.
На пути три развилки по два варианта 2·2·2=8
Ответ:0,125

№ 320194 В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение:
- всего рейсов.
Попасть на первый рейс (равно как и на второй и на любой
имеющийся) – один шанс из пяти .
Ответ:0,2

№ 320186 На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Решение:
Возможные комбинации (независимо от количества групп):
ШНД
ДШН
ДНШ
6 - вариантов
НДШ
ШДН
НШД
Благоприятных - 2
Ответ:0,33

№ 320196 При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Решение:
А – диаметр не больше 66,99 и не меньше 67,1
Р(А) =0,965
Диаметр меньше чем 66,99 мм или больше чем 67,01 мм – противоположное событие
Ответ:0,035

№ 320191 На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение:
- участников не попали в
первые две аудитории
Только 10 из 250 участников имеют шанс попасть в
запасную аудиторию.
Ответ:0,04
 Р(ничья)=1-Р(выиграла)-Р(проиграла)=1-0,4-0,4=0,2" width="640"
Р(ничья)=1-Р(выиграла)-Р(проиграла)=1-0,4-0,4=0,2" width="640"
№ 320188 Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
События «ничья», «выиграла», «проиграла» составляют
полную группу.
=Р(ничья)=1-Р(выиграла)-Р(проиграла)=1-0,4-0,4=0,2

№ 320188 Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Условию удовлетворяют три независимых события:
А – команда выиграла в первой и во второй игре. Р(А)=0,4∙0,4=0,16
В – команда выиграла в первой игре и во второй сыграла вничью. Р(В)=0,2∙0,4=0,08
С – команда выиграла во второй игре и в первой сыграла вничью Р(С)= 0,2∙0,4=0,08
А, В, С -несовместны
Ответ:0,32

Задачи открытого банка.
Сумма несовместных событий.

№ 319171 На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Событие А – вопрос на тему «Вписанная окружность»
Событие В – вопрос на тему «Параллелограмм»
События А и В – несовместны. (Если достался первый, то не достался второй.)
Ответ:0,35

№ 320203 Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение:
В=А+С
А и С - несовместны
Ответ:0,38

№ 320198 Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Решение:
С=А+В
А и В - несовместны
Ответ:0,07

Задачи открытого банка.
Произведение совместных событий.

№ 320183 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение:
Событие А – жребий выигран ровно два раза
Возможные исходы, удовлетворяющие условию:
1 игра – жребий выигран Р=0,5 (Вероятность орла=0,5)
2 игра – жребий выигран Р=0,5 (Вероятность орла=0,5)
3 игра – жребий не выигран Р=0,5 (Вероятность решки=0,5)
Порядок игр в данной задаче не имеет значения. События совместны.
Ответ:0,125
Р(А)=0,5∙0,5∙0,5=0,125

№ 320210 Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
События А 1 и А 2 - совместны
Ответ:0,8836

№ 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение:
Лучше переформулировать задачу.
Сколько выстрелов (n) надо сделать, чтобы вероятность непопадания была меньше или равна 0,02 (1-0,98)
Событие А – первый раз не попал. Р(А)=1-0,4=0,6

№ 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение:
Тогда рассматриваем события – не попал при следующих выстрелах (возможны если не попал первый раз т. е. к-во событий =n-1). P=1-0,6=0,4
Перебором определяем n.
n=5
Ответ: 5

№ 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение(второй способ):
Вероятность промаха при первом выстреле равна 1-0,4=0,6
Вероятность промаха при каждом следующем выстреле
равна 1-0,6=0,4
Будем стрелять, пока вероятность промаха будет менее 0,02 (1-0,98 – вероятность не уничтожения цели)
0,6∙0,4∙0,4∙∙∙
Ответ: 5

№ 319175 Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит .
Решение:
Вероятность того, что перегорят обе лампы равна 0,3∙0,3=0,09
Событие – не перегорела хотя бы одна лампа – противоположное.
Его вероятность равна 1-0,09=0,81
Ответ:0,81
 (вероятность непопадания) Все пять событий совместны Р=0,8∙0,8∙0,8∙0,2∙ 0,2=0,02048 Ответ:0,02048" width="640"
(вероятность непопадания) Все пять событий совместны Р=0,8∙0,8∙0,8∙0,2∙ 0,2=0,02048 Ответ:0,02048" width="640"
№ 319173 Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение:
Событие А – попал.
Р(А) =0,8
Р(А) =0,8 =
(вероятность непопадания)
Все пять событий совместны
Р=0,8∙0,8∙0,8∙0,2∙ 0,2=0,02048
Ответ:0,02048

Задачи открытого банка.
Произведение совместных событий и сумма несовместных.

№ 320211 Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная из упаковки батарейка будет забракована.
Решение:

Решение:
Возможные благоприятные для задачи события
Исправная батарейка
Неисправная батарейка
забракована (совместны)
забракована (совместны)
Батарейка исправна и неисправна – несовместны, значит событие – забракована
исправная и забракована неисправная – несовместны.
Ответ:0,0296

№ 320207 Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение:

Решение:
Р(А 1 ) =5%:100%=0,05
А 1 – поступил пациент с гепатитом
В 1 – у больного гепатитом положительный анализ
Р(В 1 ) =0,9
Р(А 2 ) =1-0,05=0,95
А 2 – поступил здоровый пациент
Р(В 2 ) =0,01
В 2 – у здорового пациента положительный анализ
Возможные благоприятные для задачи события
Поступил здоровый и анализ
Поступил больной и анализ
положительный
положительный
А 2 и В 2 – совместны
А 1 и В 1 – совместны
Эти события несовместны
Ответ:0,0545

Шутка от составителей тренировочных работ на сайте
alexlarin.com (убрали одну стенку).
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу А.
Решение:
к выходу А синим путем.
Три развилки с двумя
вариантами исходов.
Р 1 =0,5∙0,5∙0,5=0,125
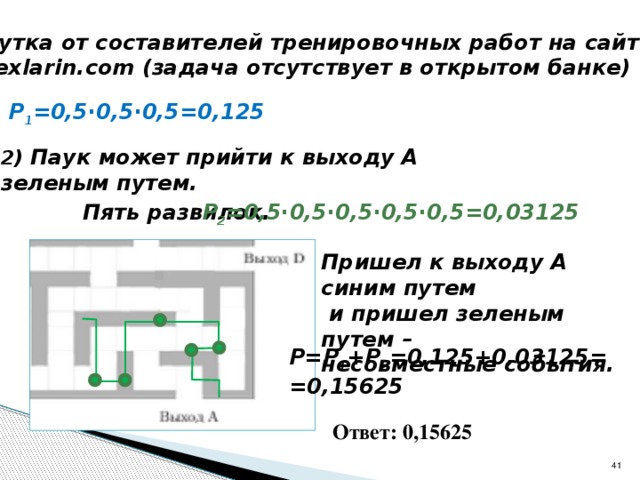
Шутка от составителей тренировочных работ на сайте
alexlarin.com (задача отсутствует в открытом банке)
Р 1 =0,5∙0,5∙0,5=0,125
2) Паук может прийти к выходу А
зеленым путем.
Р 2 =0,5∙0,5∙0,5∙0,5∙0,5=0,03125
Пять развилок.
Пришел к выходу А синим путем
и пришел зеленым путем –
несовместные события.
Р=Р 1 +Р 2 =0,125+0,03125=
=0,15625
Ответ: 0,15625

№ 320206 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
А 4 – 4 июля хорошая погода. Р(А 4 )=0,8
В 4 – 4 июля отличная погода. Р(В 4 )=1-0,8=0,2
А 5 – 5 июля хорошая погода. Р(А 5 )=
0,8·0,8+0,2·0,2=0,68
В 5 – 5 июля отличная погода. Р(В 5 )=
0,2·0,8+0,8·0,2=0,32
В 6 – 6 июля отличная погода. Р(В 6 )=
0,32·0,8+0,68·0,2=0,392
Ответ:0,392
?
 Р(А 5 ) = сумме вероятностей двух событий" width="640"
Р(А 5 ) = сумме вероятностей двух событий" width="640"
Событие А 5 – 5 июля хорошая погода возможно в двух случаях.
Была хорошая и осталась такой. Вероятность=0,8·0,8 (была и осталась – совместные события)
Была отличная и изменилась.
Вероятность=0,2·0,2 (была и изменилась – совместные события)
Случаи несовместны =
Р(А 5 ) = сумме вероятностей двух событий

№ 320199 Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение:

Решение:
А – набрано не менее 70 баллов по математике. Р(А)=0,6
В – набрано не менее 70 баллов по русск. языку. Р(В)=0,8
С – набрано не менее 70 баллов по англ. языку. Р(С)=0,7
D – набрано не менее 70 баллов по обществозн. Р(D)=0,5
Все эти события совместны
Вероятность поступления только на «Лингв.» =
0,6·0,8·0,7·(1-0,5)=0,168
Вероятность поступления только на «Комм.» =
Все эти события несовме
стны
0,6·0,8·0,5∙(1-0,7)=0,072
Вероятность поступления на обе специальности=
0,6·0,8·0,7·0,5=0,168
Вероятность поступления хотя бы на одну специальность =
=0,168+0,072+0,168=0,408
Ответ:0,408

№ 320180 Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение:
Вероятность непопадания из пристрелянного=1-0,9=0,1
Вероятность непопадания из непристрелянного=1-0,2=0,8
Событие А – взял пристрелянный. Р(А)=4/10=0,4
Событие В – взял непристрелянный. Р(В)=1-Р(А)=0,6

№ 320180 Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение:
Событие А 1 – взял пристрелянный и не попал. Р(А 1 )=Р(А)∙0,1=0,4∙0,1=0,04 (взял и не попал – совместные события)
Событие В 1 – взял непристрелянный и не попал. Р(В 1 )=Р(В)∙0,8=0,6∙0,8=0,48
Вероятность непопадания
Ответ:0,52

№ 319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая –– 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая –– 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Событие А –стекло выпустила первая фабрика
Р(А)=0,45
Событие В –стекло выпустила вторая фабрика
Р(В)=0,55
Событие А 1 – колесо, выпущенное первой фабрикой – бракованное.
Р(А 1 )=0,03
Событие В 1 – колесо выпущенное второй фабрикой – бракованное.
Р(В 1 )=0,01

№ 319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая –– 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая –– 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
- куплено бракованное колесо первой ф.
- куплено бракованное колесо второй ф.
Эти события - несовместны
Р=0,0135+0,0055=0,019
Ответ:0,019

Задачи открытого банка.
Статистическое определение вероятности..

№ 320189 В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Решение:
- статистическая вероятность
(частота рождения).
Ответ:0,4976

№ 320195 Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение:
вероятность.
Ответ:0,006

№ 320200 На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов.
Решение:
А – произведенная тарелка имеет дефект
Р(А) =10%:100%=0,1
В – при контроле выявлена дефектная тарелка
Р(В) =80%:100%=0,8
Вероятность того, что произвели
дефектную тарелку и обнаружили дефект =
Событие – произведена тарелка без дефекта и дефект не обнаружен противоположно предыдущему.
Его вероятность =
Ответ:0,92

№ 319177 Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение:
В задаче требуется узнать, какую часть всех яиц выпускает первое хозяйство. Это статистическая вероятность события «куплено яйцо из первого хозяйства»
Пусть х яиц выпускает первое хозяйство (0,4х – высшей кат.), у – второе (0,2у – высшей кат.).
Составим уравнение:
Значит первое хозяйство поставляет ¾ всех яиц.
Ответ:0,75

Задачи открытого банка.
Сумма совместных событий.

№ 320174 В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Событие А – исправен первый автомат Р(А)=1-0,05=0,95
Событие В – исправен второй автомат
Р(В)=1-0,05=0,95
События А и В – совместны.
А∙В – исправны оба
Р(А∙В)=0,95∙0,95=0,9025
А+В– хотя бы один исправен
Р(А+В)=Р(А)+Р(В)-Р(А)∙Р(В)=0,95+0,95-0,9025=0,9975
Ответ:0,9975

№ 319172 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
Событие А – кофе закончилось в первом автомате Р(А)=0,3
Событие В – кофе закончилось во втором автомате
Р(В)=0,3
События А и В – независимы
D – кофе закончилось в двух автоматах
Р(D)=0,12
С– кофе закончится хотя бы в одном из двух
Р(С)=Р(А)+Р(В)-Р(А)∙Р(В)=0,3+0,3-0,12=0,48
События «кофе закончилось хотя бы в одном» и «осталось в обоих» - противоположны.
Ответ:0,52
Р=1-Р(С)=0,52

Условная вероятность.

320192
В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение:
Андрей обязательно попал в какую то группу (достоверное событие) Р=1
Теперь в этой группе 12 свободных мест и осталось 25 учеников..
Сергей попал в ту же группу Р=12/25
Рассматриваемые события – совместны.
Ответ:0,48

В банке нет, но в некоторых тренировочных работах предлагается
На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие это холодильники. Найти вероятность того, что два взятых наугад холодильника будут с дефектами. Ответ округлите до сотых.
Решение:
Вероятность того, что первый взятый наугад холодильник имеет дефекты равна 5/35=1/7
Теперь из 34 холодильников 4 имеют дефекты.
Вероятность того, что второй взятый наугад холодильник имеет дефекты при условии, что один с дефектами уже взяли равна 4/34=2/14
Рассматриваемые события – совместны.
Ответ:0,02

Источники:
УМК А. Г. Мордкович (профильный уровень)
И. Л. Бродский, Р. А. Литвиненко.“Вероятность и статистика.” - М.: Аркти. - 2006.
Открытый банк задач.
Г. В. Сычева, Н. Б. Гусева “Математика. ГИА. 9 класс”
А. Г. Мордкович “Алгебра и начала анализа. Профильный уровень. 10 класс.”
http://ta-shah.ucoz.ru/load
http://www.mccme.ru/free-books/shen/shen-probability.pdf
http://www.matburo.ru/tvbook_sub.php?p=par14
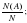 оно и будет равно вероятности события А.
оно и будет равно вероятности события А.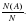
 Р(А) =
Р(А) = 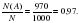
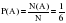 .
.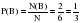 .
.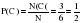 .
.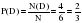 .
. 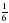 ; б)
; б) 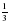 ; в)
; в) 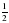 ; г)
; г) 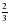 .
.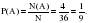
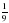 .
.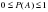 .
.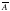 . Сумма вероятностей противоположных событий равна 1.
. Сумма вероятностей противоположных событий равна 1. 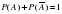 .
.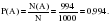
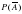 =
= 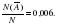 Значит,
Значит, 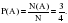
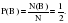
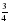 ; б)
; б) 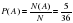 .
.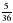 .
.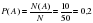 .
.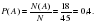
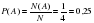
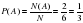
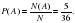
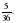
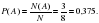
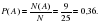
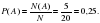
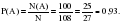




















 Р(ничья)=1-Р(выиграла)-Р(проиграла)=1-0,4-0,4=0,2" width="640"
Р(ничья)=1-Р(выиграла)-Р(проиграла)=1-0,4-0,4=0,2" width="640"












 (вероятность непопадания) Все пять событий совместны Р=0,8∙0,8∙0,8∙0,2∙ 0,2=0,02048 Ответ:0,02048" width="640"
(вероятность непопадания) Все пять событий совместны Р=0,8∙0,8∙0,8∙0,2∙ 0,2=0,02048 Ответ:0,02048" width="640"








 Р(А 5 ) = сумме вероятностей двух событий" width="640"
Р(А 5 ) = сумме вероятностей двух событий" width="640"






































