М униципальное бюджетное образовательное учреждение
униципальное бюджетное образовательное учреждение
«Нижнекондратинская средняя общеобразовательная школа»
Чистопольского района Республики Татарстан

Урок по геометрии в 11 классе
«Объём прямоугольного параллелепипеда»
УМК Л.С.Атанасян и др.
Учитель:
Плотникова Л.Г.
Тема урока «Объём прямоугольного параллелепипеда. Решение задач»
Урок разработан с применением модульной технологии обучения и ИКТ. Рассчитан на 2 академических часа.
Цель урока: Выработка умений и навыков учащихся решать задачи на вычисление объёма прямоугольного параллелепипеда, применяя различные формулы для вычисления площади прямоугольников. Рассмотреть решение задач на вычисления объёма прямоугольного параллелепипеда при помощи многогранников. Провести срез знаний по данной теме.
Вид урока: урок – тренинг (закрепление знаний).
Оборудование: компьютер, проектор, слайды, чертёжные инструменты, цветные мелки.
Ход урока
УЭ – 0 Мотивация
Учитель объявляет тему и формулирует совместно с учениками цель урока.
Что такое объём?
Как вычислить объём прямоугольного параллелепипеда.
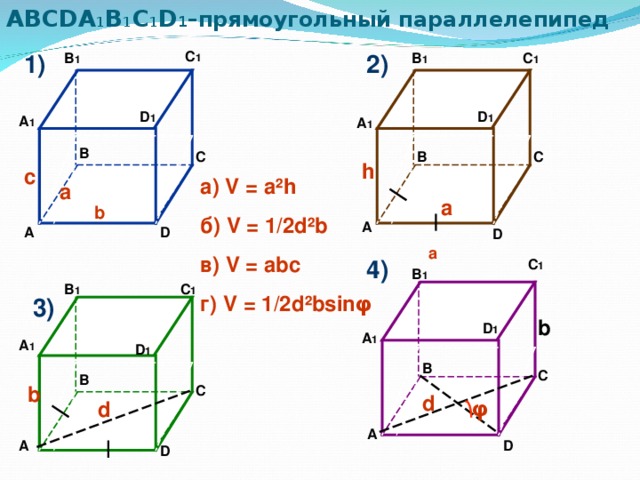
УЭ – 1 Установите соответствие между параллелепипедом и формулой (слайд 2)
Вопросы учителя:
Назовите «универсальную» формулы для вычисления объёма прямоугольного параллелепипеда?
А какая формула для вычисления объёма не использовалась?
Нельзя ли её применить для вычисления объёма прямоугольного параллелепипеда изображенного на рисунке 2 или 3?
УЭ - 2
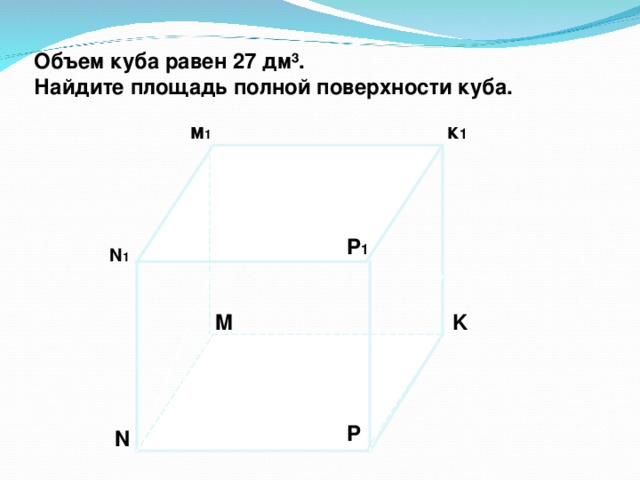
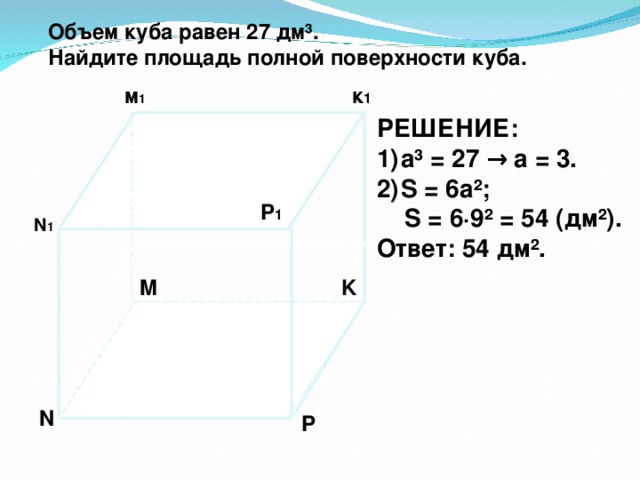
1.Объём куба равен 27дм3.Найдите площадь полной поверхности куба.
(слайд 3)
Проверить по ключу.
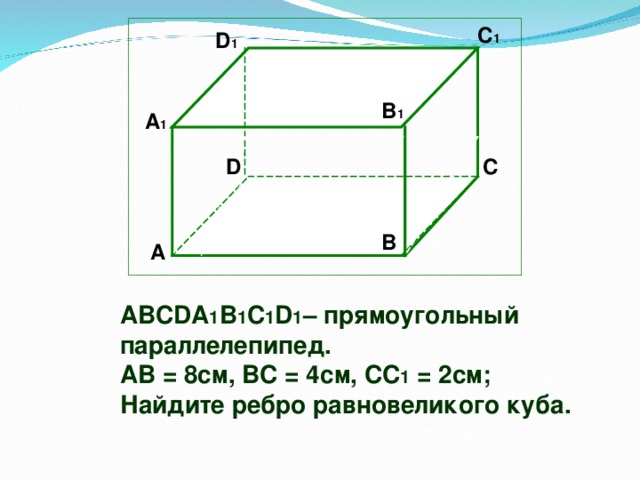
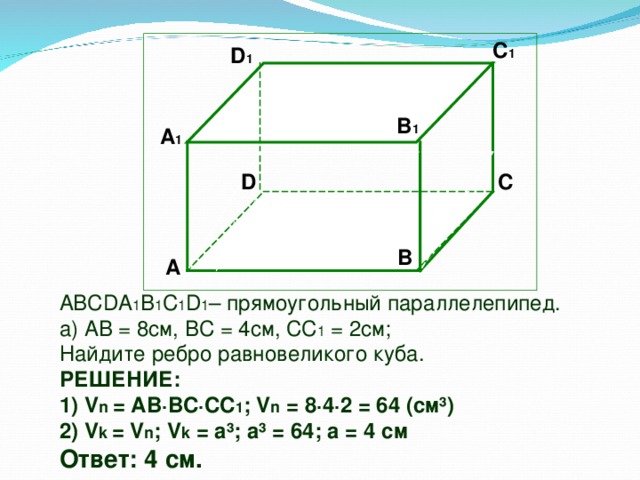
2.В прямоугольном параллелепипеде АВСDА1В1С1D1
АВ=8см; ВС=4см;СС1=2см. Найдите ребро равновеликого куба.
(слайд 4)
Проверить по ключу.
УЭ- 3
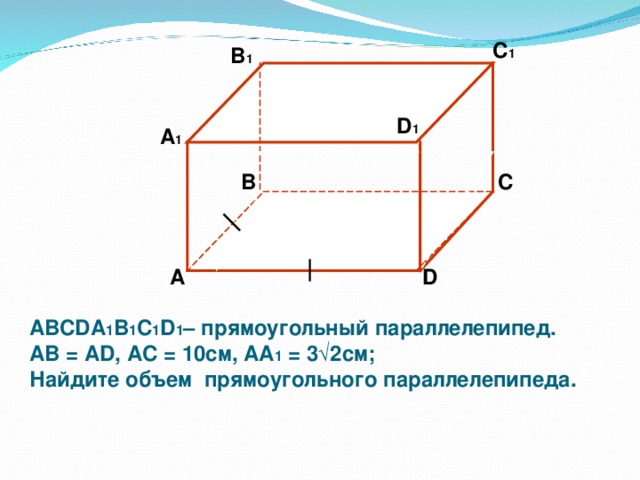
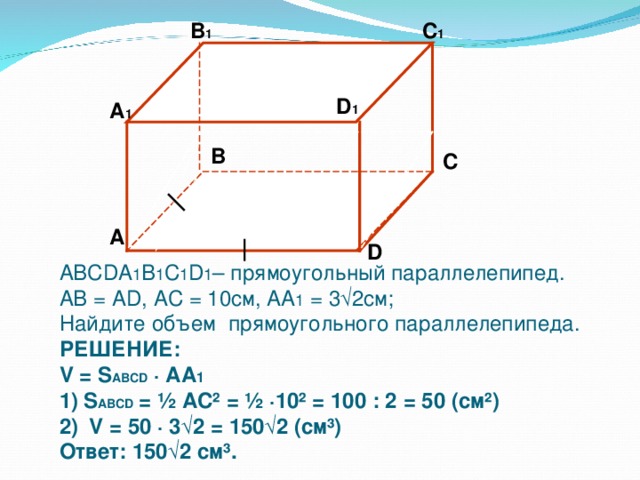
1. В прямоугольном параллелепипеде АВСDА1В1С1D1, АВ=АD; АС=10см; АА1=3√2см. Найдите объём.
(Учитель совместно с учащимися анализирует условие и составляет план решений, а затем после самостоятельной деятельности учащихся проверит по ключу)
(слайд 5)
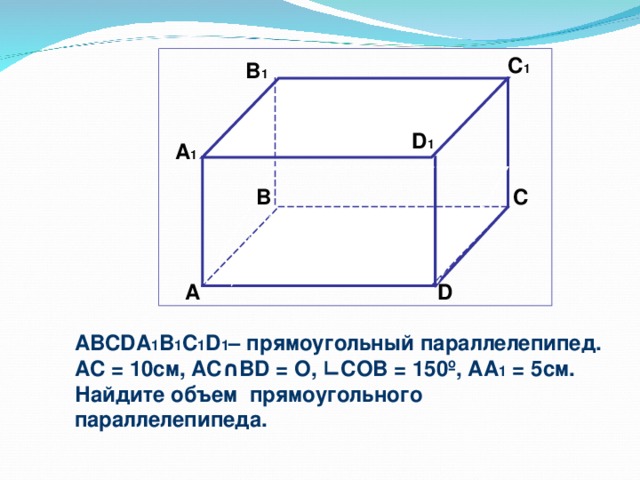
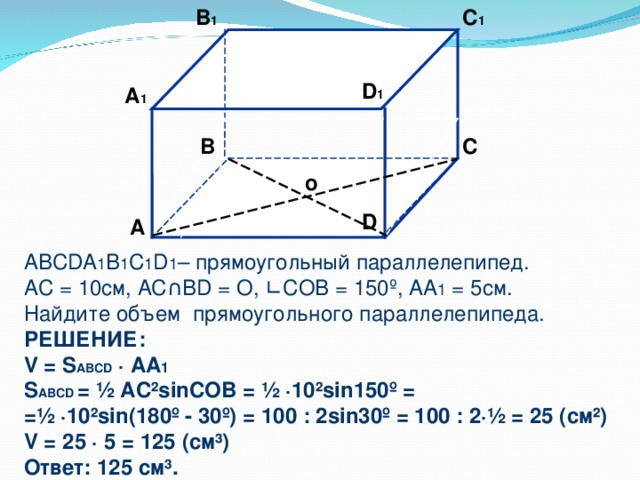
2. АВСDА1В1С1D1 - прямоугольный параллелепипед АС∩ВД=0,∟СОB=1500, АА1=5см; АС=10см
Найдите объём прямоугольного параллелепипеда.
(Учитель совместно с учащимися анализирует условие и составляет план решений, а затем после самостоятельной деятельности учащихся проверит по ключу)
(Слайд6)
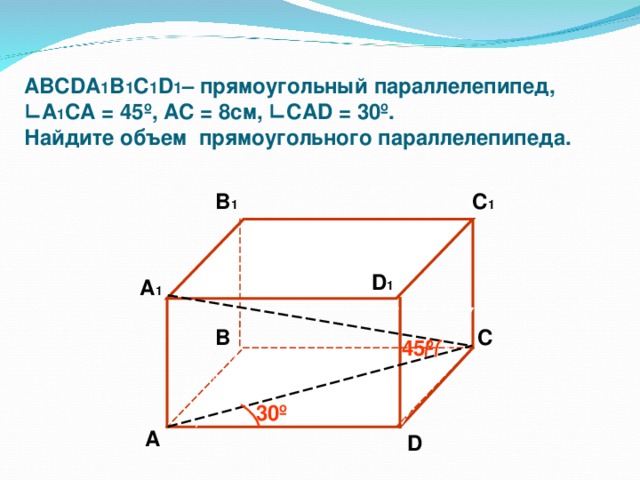
УЭ - 4 По данному чертежу составьте задачу.
(Слайд7)
УЭ - 5
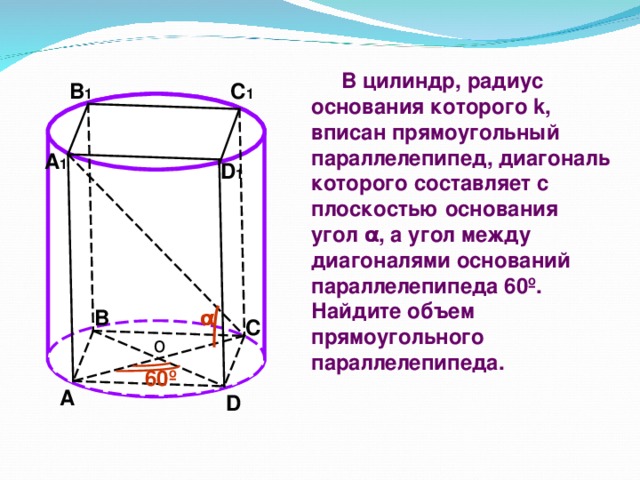
В цилиндр, радиусом основания которого равен R, вписан прямоугольный параллелепипед, диагональ которого составляет с плоскостью основания угол L , а угол между диагоналями основания параллелепипеда 600.
Найдите объём прямоугольного параллелепипеда.
(Слайд8)
/Решите на доске/
УЭ - 6 «Математические развлечения»
I. Кто быстрее?
А) Слова на букву «К»
1.Геометрическая фигура.
2.Произведение гипотенузы на косинус прилежащего угла.
3.Прямая, имеющая с окружностью только одну общую точку.
4.Отношение прилежащего катета к гипотенузе.
Б) Слова на букву «П»
1)Наука, изучающая свойства фигур на плоскости.
2) Если 36см2 = S кв, то 24 см - ?
3) Геометрическая фигура, все углы которой равны.
4) Отрезок, соединяющий основание наклонной и перпендикуляра.
II. Кто больше? За 2 мин записать формулы для вычисления площади
треугольника прямоугольника
УЭ – 7 Решить задачи.
1.В шар радиуса R вписан прямоугольный параллелепипед, диагональ которого составляет с одной из граней угол α , угол между диагональю этой грани и стороной основания 60°.Найдите объем параллелепипеда.
(R3√3cosα sin2α)
2.В прямоугольном параллелепипеде помещены 2 шара радиуса k так, что каждый касается другого шара и пяти граней параллелепипеда. Найдите объём параллелепипеда. (16k³)
УЭ – 8 Итоги урока и домашнее задание.
№ 656 – слайд, на котором показано построение линейного угла.
№ 658 – V = Sосн.· H
 униципальное бюджетное образовательное учреждение
униципальное бюджетное образовательное учреждение