Конспект урока по математике "Умножение на двузначное число"

Деятельность учителя

Деятельность ученика

УУД

Л- личностные

П- познавательные

Р- регулятивные

К- коммуникативные

I. Организационный момент. Эмоциональный настрой:

«Если знаешь – помогай, а не знаешь – слушай». Самоопределение к учебной деятельности (мотивация)

Дети пожимают друг другу руки – ты мой друг!

Самоопроеделение к деятельности – (Л);

II. Актуализация опорных знаний, фиксирование затруднений в деятельности

Сегодня мы продолжаем работать по теме « Умножение многозначных чисел».

163*45

(Работа в группах.)

- Попробуйте найти значение данного выражения.

- Запишите свой вариант на доске.

- Объясните свое решение.

1. Заменю второй множитель суммой разрядных слагаемых. Используя распределительное свойство умножения;

число 163 умножу на каждое из этих слагаемых и полученные результаты сложу.

2. Используя переместительное свойство умножения, записываю: 45х163.

Число 163 заменю суммой разрядных слагаемых.

Используя распределительное свойство умножения, число 45 умножу на каждое из слагаемых. Полученные результаты сложу.

3. Второй множитель заменю произведением 9 и 5.

Используя сочетательное свойство умножения 163х9, полученный результат умножу на 5, получу 7335.

-смыслообразование (Л);

-Мыслительные операции(обобщ, анализ, синтез, сравнение)-П;

III. Постановка учебной задачи

– Задание для вас оказалось простым или сложным?

– В чем заключалась трудность?

- Что отрицательного, на ваш взгляд, в данных способах записи решения?

– Что делать?

- Какой выход можете предложить?

– Может, есть другой способ записи, чтобы было легко, просто, да к тому же быстро и удобно?

Выход на тему урока

Что вам хочется узнать?

Используйте вопросы любознательных детей.

Как?

Зачем? – Цели определены.

Где?

– Попробуйте выполнить вычисления в столбик.

- Подумайте, как это сделать?

Затрачиваем много времени.

Запись в столбик.

- целеполагание - (П);

- планирование учебного сотрудничества с учителем и сверстниками(К);

-фиксирование инд.затруднений в пробном учебном действии - Р;

-волевая саморегуляция в затруднении – Р;

-выражение своих мыслей с достаточной полнотой и точностью – К;

-аргументирование своего мнения и позиции в коммуникации- К .

IV. Поиск способа действий. Решение учебной задачи

(Работа в паре) См. Прил. 1.

– Почему получили разные результаты?

– Какой результат должны получить? Почему?

– Давайте порассуждаем.

– Что делаем сначала?

Варианты, предложенные детьми.

Умножаем первый множитель на число единиц второго множителя.

Извлечение из предметного текста необходимой информации - П;

- Использование знаково- символических средств (схем, чертежей и др.) -П;

-осознанное и произвольное речевые высказывание – П;

Построение логической цепи рассуждений и доказательств +КУУД 4 этапа.

Опорная таблица. См. Прил. 2.

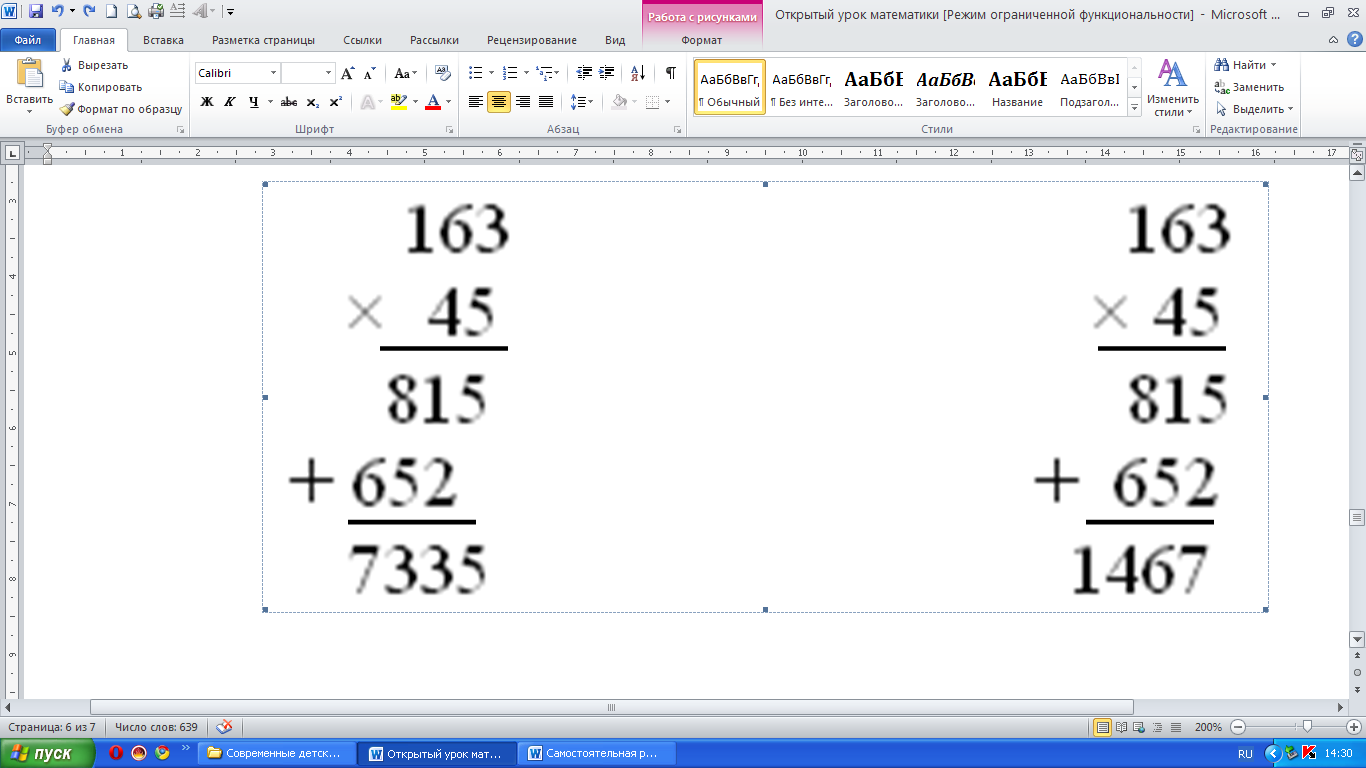
– Чему равно произведение?

– Это окончательный результат?

– Как можно назвать такое произведение?

– Что делаем затем?

– Что получаем?

– Какое свойство умножения использовали?

– Что заметили, сравнивая обе эти записи?

– Какая запись на ваш взгляд верна? Почему?

– Из чего видно, что записано 652 десятка?

(Учитель приписывает справа 0).

– Можно 0 не писать и оставить так, как было? Почему?

(0 стирается).

– При сложении числа единиц первого неполного произведения с нулем, это число не изменится, поэтому 0 на конце второго неполного произведения не пишут, но всегда оставляют для него место.

– Почему в другом случае получили ошибочный результат?

– Чем удобна запись в столбик?

– Умножение в столбик – это действительно удобно, легко, просто при условии, что мы четко знаем алгоритм и действуем в соответствии с ним.

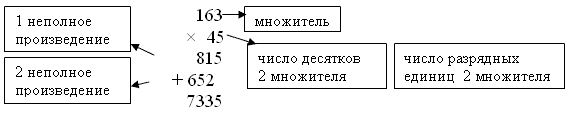
– Попробуйте составить алгоритм умножения многозначных чисел на двузначное число в столбик.

(Алгоритм появляется на доске на отдельных листах)

1. Умножу 1 множитель на число разрядных единиц 2 множителя.

Получу 1 неполное произведение.

2. Умножу 1 множитель на число десятков второго множителя.

Получу 2 неполное произведение.

– Что должны помнить при записи 2 неполного произведения?

3. Сложу неполные произведения.

– Хорошо. Давайте проверим совпадает ли наш способ действий с выводами ученых?

– Молодцы! Вместе мы преодолеем любые трудности.

Первое неполное произведение

Умножаем первый множитель на число десятков второго множителя.

Второе неполное произведение

Распределительное.

Верна первая запись. Умножали на 4 десятка, значит, получили 652 десятка, а во второй записи 652 единицы.

Первое место справа оставлено для разрядных единиц. 652 десятка– 6520 единицы.

Результат не изменится.

Неверно подписали второе неполное произведение. Его нужно записывать левее, оставляя место для единиц.

Удобно, быстро, легко.

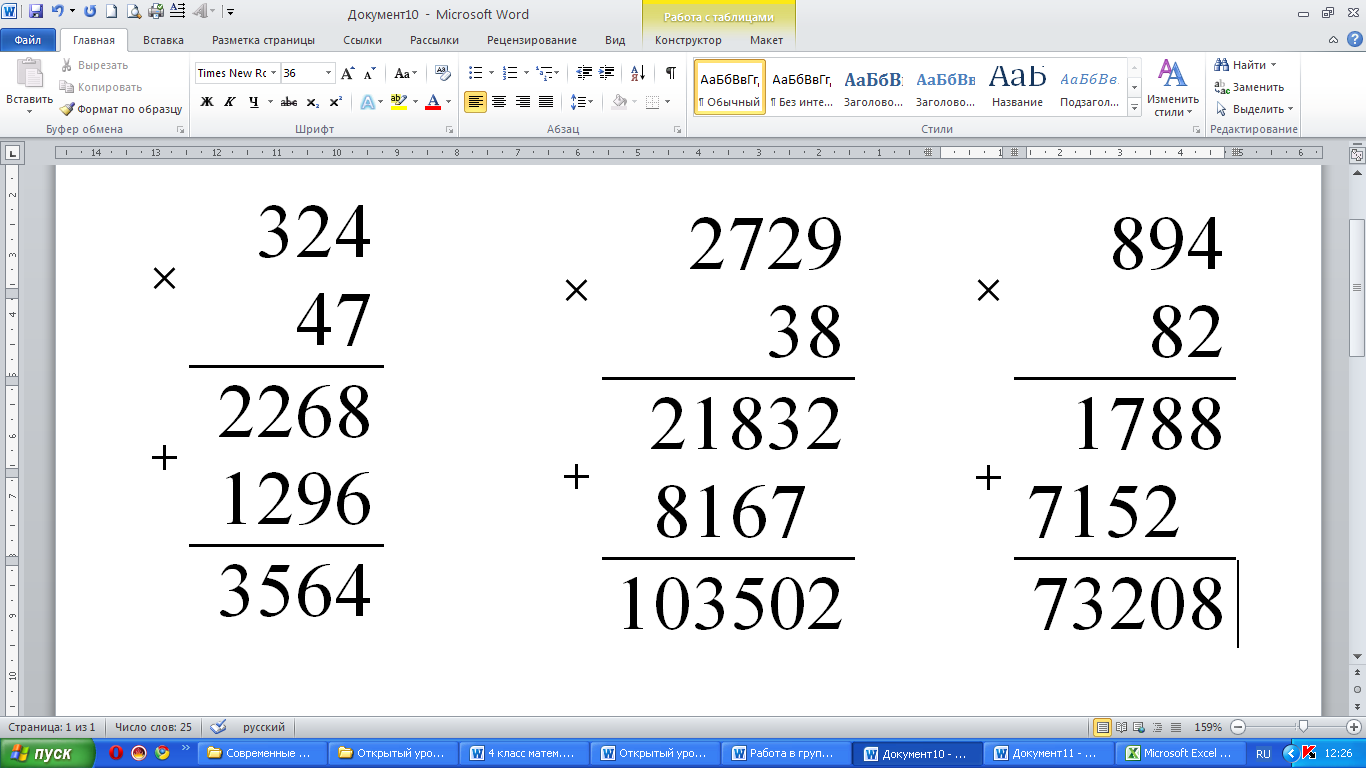
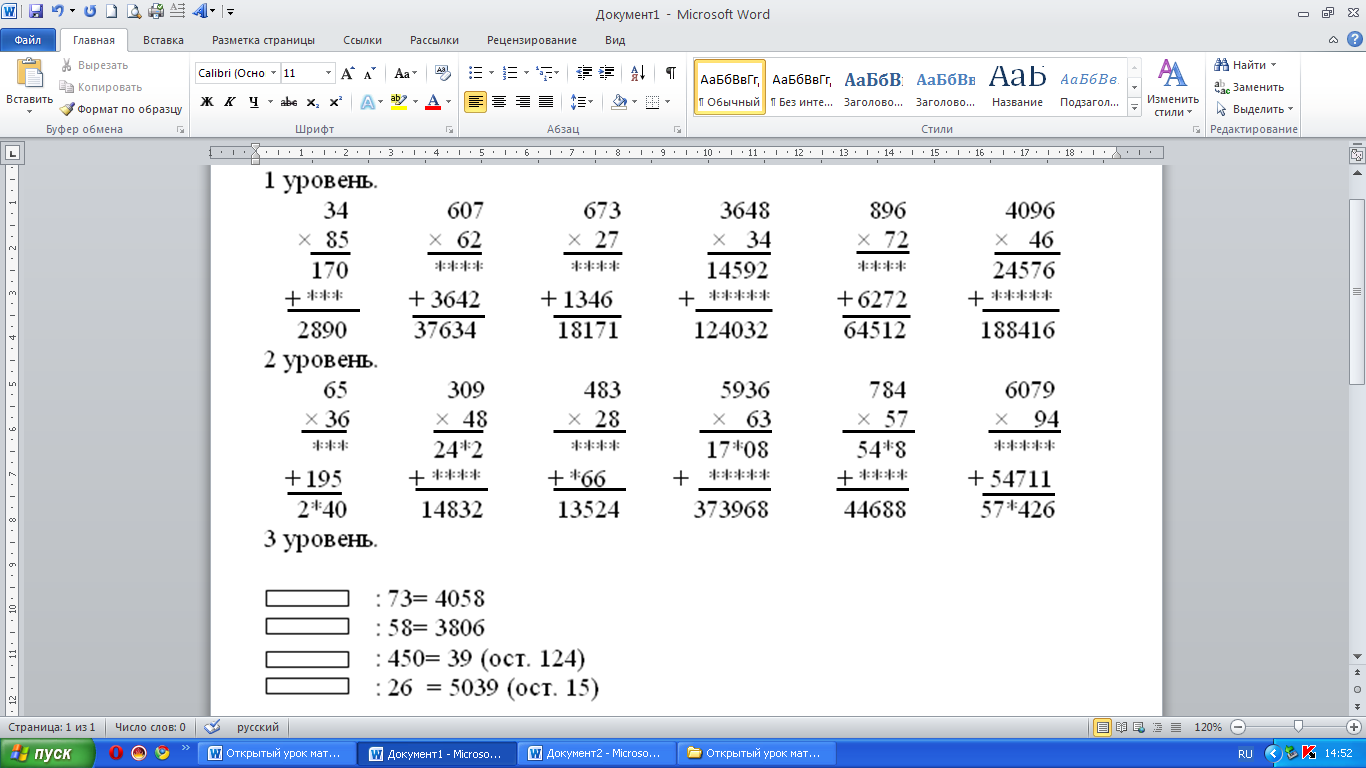
Работа в группах.

Открываем учебник, с. 35

V. Применение открытого способа действий

(Работа в группах.) См. Прил.3.

– Найди ошибки и исправь

1. Неверно подписано второе неполное произведение.

2. Ошибка допущена при нахождении второго неполного произведения.

3. Ошибка при сложении двух неполных произведений.

-осознанное и произвольное речевые высказывание – П;

-построение логической цепи рассуждений.

Коммуникативные УУД:

• учебное сотрудничество с учителем и одноклассниками

• работа в парах

Самостоятельная работа.

См. прил. 4.

(Предлагается материал разной степени сложности в зависимости от уровня подготовленности учащихся.)

VI. Итог

– Вернёмся к началу урока.

– В чём испытывали затруднения?

– Как умножить многозначное число на двузначное в столбик?

Рефлексия способов и условий действий – П;

-контроль и оценка способов своей деятельности -Р;

-самооценка на основе критерий успешности-Л;

- адекватное понимание успешности или неуспешности;

-- выражение своих мыслей с достаточной полнотой и точностью –К;

- планирование успешного сострудничества - К

- следование моральным нормам и этическим требованиям - Л

VII. Домашнее задание

-Составить выражения по теме

-Задачу при решении

- с.36 №170. №175