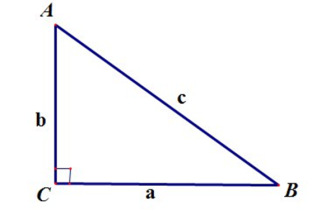
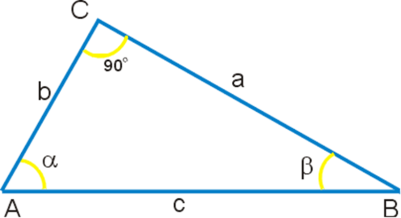
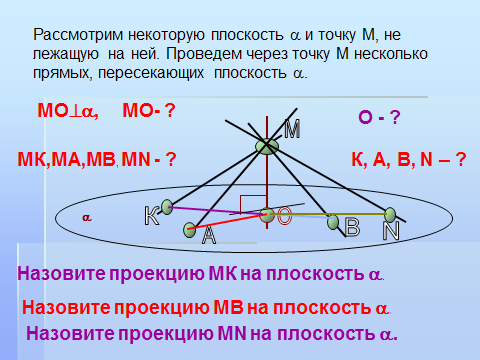
Тема урока: "Угол между прямой и плоскостью." Тип урока: урок применения и закрепления знаний. Цели: повторить понятия перпендикуяра, наклонной и ее проекции, алгоритм нахождения угла между прямой и плоскостью, развивать пространственное воображение и воспитыать интерес к предмету. Конспект урока содержит задачи на повторение из курса планиметрии, задания на повторение теоритического материала и задачи в которых необходимо уметь находить углы между прямой и плоскостью. Конспет содержит задачи практического содержания по данной теме.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
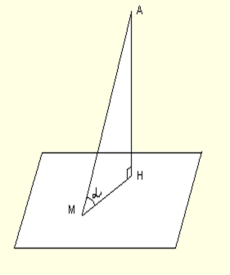
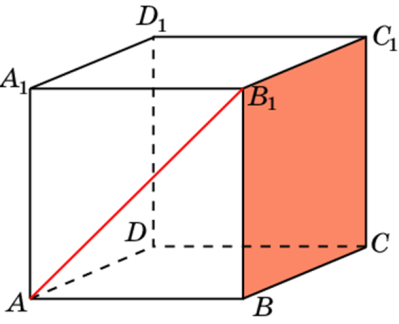
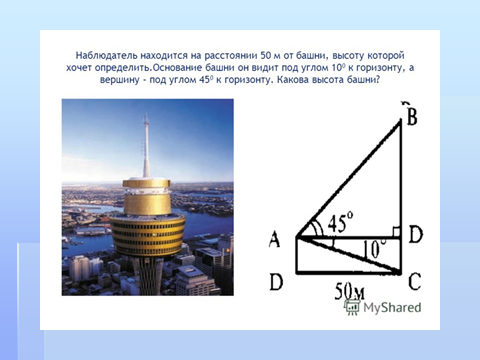
Конспект урока по теме "Угол между прямой и плоскостью. Решение задач".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока по теме "Угол между прямой и плоскостью. Решение задач". »
Полезное для учителя
Распродажа видеоуроков!
1850 руб.
2640 руб.
1650 руб.
2350 руб.
1450 руб.
2070 руб.
1580 руб.
2260 руб.
Курсы ПК и ППК для учителей!
500 руб.
2500 руб.
800 руб.
4000 руб.
2760 руб.
13800 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства