О проведении уроков «Анализ контрольной работы».(2 версия)
В изучении математики важно не допустить пробелов в знаниях и умениях учащихся. Контрольная работа предполагает
проверить качество знаний и умений учащихся.
Цель урока «Анализ контрольной работы»-установить и проработать типичные ошибки,повторить и систематизировать знания и умения по тем разделам программы в которых допущено наибольшее колличество ошибок.
Задачи урока-понять причину полученных ошибок,исправить их и выполнить аналогичные задания,научить приобретать знания самостоятельно.
Форма учебной работы-дифференцированно-групповая,индивидуальная.
Проверка работы идет параллельно с заполнение листа контроля,где отражены ошибки детей по каждому заданию,оценка за контрольную и самостоятельную работу,тест,зачет.Лист контроля позволяет в дальнейшем четко определить индивидуальную работу с учащимися,которые делятся на три группы:1)выполнили работу без ошибок,2)с единичными ошибками,3)не справились с работой.
Урок «Анализ контрольной работы» проходит следующим образом:
1).Устный счет-включены основные моменты теории и примеры,отрабатывающие их.
2).На экране показана выполненная контрольная работа с теми заданиями ,где допущены ошибки.
Учащиеся первой и второй групп находят ошибки у себя в тетради и с места комментируют решение. Эта часть работы проходит очень активно и заинтересованно,учащиеся стараются выяснить все непонятные вопросы.
3)Проводится мини-тест,который содержит задания с учетом ошибок,допущенных в контрольной работе.
4).Учащиеся,справившиеся с контрольной работой (3группы),помогают его проверять.
5).Разбираются вновь или повторно допущенные ошибки.
6).Проводится самостоятельная работа по индивидуальным карточкам.
Для учащихся,не усвоивших тему,проводится урок –консультация ,затем зачет,который включает вопросы и задания обязательных результатов обучения.
Практикую и такую форму урока:
Выдаю тетради без исправленных ошибок и оценок,(результаты проверки записаны в планах).На экране показываю подробное решение каждого варианта.Учащиеся карандашом исправляют ошибки,сопоставляя свои решения с решениями на экране.Те задания ,которые они решили полностью неверно или не решили,записывают в тетради для контрольных работ,затем ставят себе оценку за контрольную работу и сдают тетрадь. Те дети,которые справились с контрольной работой,решают задания повышенной сложности.Затем учащиеся еще раз просматривают решения заданий на экране и пишут самостоятельную работу.Оценка в журнал ставится с учетом проведенной работы над ошибками. Такая форма работы с учащимися позволяет не только ликвидировать пробелы в знаниях учащихся,но имеет и воспитательное значение.Ребята учатся добиваться цели,доводить дело до конца,отрабатывать навыки самостоятельной работы и четко организуют взаимопомощь.
М.Р.Семенихина.
Зачет в старших классах.
Практикую зачеты по геометрии: открытые и тематические.
Зачет состоит из двух частей:теоретической и практической.Вопросы зачета вывешиваю в самом начале изучаемой темы.Теоретическую часть учащиеся сдают устно. Практическая часть состоит из трёх задач. Класс делится на 4 группы. Каждому ученику дается своя карточка с обязательным и дополнительным заданием. Время на выполнение работы 30 минут,на проверку-10 минут,на подведение итогов-5 минут. Итоги подводят консультанты.
Такая форма организации зачёта даёт всем равные возможности для достижения хороших результатов. Хорошо успевающие учащиеся уже на этапе самостоятельной работы могут показать высокий результат.Далее они продолжают закреплять полученные знания,работая со своими группами. Остальные учащиеся имеют возможность сдать зачёт своим консультантам.
Меняя место зачёта в системе проверки знаний. Сначала предлагаю контрольную работу. Успешно справившихся с ней освобождаю от зачёта. Зачёт в основном сдают те,кто нуждался во время контрольной работы в дополнительном времени. Им оно предоставляется. С такими ребятами имею возможность побеседовать индивидуально и выявить пробелы в знаниях,которые тут же можно поправить.
Особый интерес представляют творческие зачёты по геометрии:”Решение одной задачи”,”Презентация темы”.
К 10-ому классу у учеников складывается определенная система знаний и умений,а в социальном плане появляется желание самоутвердиться. Такую возможность им предоставляет зачёт-экстерн. Например,при изучении темы “Круглые тела” ученики заранее знакомятся с планом работы: цилиндр,конус,контрольная работа,шар.К началу изучения темы “Цилиндр” и “Конус”,самостоятельно изучить тему “Шар” и приготовить презентацию.В ходе подготовки к зачёту планируются консультации. Для сдачи зачёта приходят учащиеся одной группы(4 человека).Каждый ученик отвечает теорию у доски,затем решает 2 задачи.Одна из них из предложенных к зачёту,другая-из дедактических материалов по геометрии.Информация о ходе сдачи зачёта показана в уголке. При такой форме организации зачёта каждый ученик имеет право выбора:работать со всем классом или изучать тему самостоятельно.
О проектах.(дополнение)
Важным аспектом в работе современного учителя является творческая активность и индивидуальные особенности каждого ребенка.Умение учащихся самостоятельно добывать знания и совершенствовать их намного важнее прочности приобретенных знаний.Приобщение учащихся к проектной деятельности и использование компъютерно-информационных технологий позволяет наиболее полно определять и развивать интеллектуальные и творческие способности.
В своей практике я использую метод проектов с 2010г. при изучении геометрии в 8-9 классах ,стереометрии,прикладных тем курса алгебры и начал анализа в 10-11 профильных классах.
В основу метода проектов положена идея о направленности учебно-познавательной деятельности учащихся на результат,который получается при решении практической или теоретически значимой проблемы.
Проектную деятельность учащихся начинаюс 9 класса,но подготовительная работа идет с 8 класса.
Первые проекты мои учащиеся делают в 8 классе по теме « Симметрия».При прохождении этой темы отмечается творческая активность и заинтересованность каждого ученика. На уроках активно формируются все ключевые компетенции.Активная форма организации труда позволяют поддерживать интерес к предмету. Практикую групповые и индивидуальные проекты.
Проекты в старших классах учащиеся выполняют в виде творческих работ-компъютерных презентаций.Это индивидуальные проекты.
Цель проектной деятельности:создание образовательной среды,способствующей формированию опыта проектной деятельности учащихся.
Задачи:
-формировать интересы,склонности учащихся к познавательной деятельности,практические умения и навыки проведения проектной деятельности
-развивать интерес и память
-развивать умение самостоятельно мыслить и использовать это умение на практике
-развивать способность излагать и защищать собственную точку зрения по проблеме
-способствовать мотивированному выбору своей деятельности и социальной адаптации учащихся.
Положительные моменты: учащиеся лучше усваивают материал,уроки стали интереснее,используют свои знания и умения,полученные на уроках ИКТ.
Мотивация обучения:интерес к предмету,к практическому материалу.
Работы по теме : «Многогранники» отражают развитие теории многогранников,знакомят с разнообразным миром многогранников,содержат фотографии моделей ,сделанных руками учащихся. «Симметрия»-содержат сведения о симметрии фигур на плоскости,симметрии для пространственных тел,симметрию в природе,в архитектуре,в убранстве и узорах различных музеев и памятников архитектуры.В 10-м классе на уроке по теме «Применение производной» учащиеся создали проект-компъютерную презентацию «Применение производной в физике и технике».
Работа над проектами проходит в 3 этапа:
1)Организационный:выбор темы,подбор литературы.
2)Основной:составление плана,подбор материала,решение задач.
3)Заключительный:оформление работ,презентация,защита презентации.
При защите презентации учащиеся демонстрируют и комментируют глубину разработки поставленной проблемы,ее актуальность. Одноклассники с интересом смотрят рабоы друг друга и оценивают их.
В данный момент идет пополнение методической копилки уроков и внеклассных мероприятий с использованием ИКТ и проектных работ учащихся,распространение опыта в работе с учащимися других классов.
Просмотр содержимого документа
«Из опыта работы»
О проведении уроков «Анализ контрольной работы».(2 версия)
В изучении математики важно не допустить пробелов в знаниях и умениях учащихся. Контрольная работа предполагает
проверить качество знаний и умений учащихся.
Цель урока «Анализ контрольной работы»-установить и проработать типичные ошибки,повторить и систематизировать знания и умения по тем разделам программы в которых допущено наибольшее колличество ошибок.
Задачи урока-понять причину полученных ошибок,исправить их и выполнить аналогичные задания,научить приобретать знания самостоятельно.
Форма учебной работы-дифференцированно-групповая,индивидуальная.
Проверка работы идет параллельно с заполнение листа контроля,где отражены ошибки детей по каждому заданию,оценка за контрольную и самостоятельную работу,тест,зачет.Лист контроля позволяет в дальнейшем четко определить индивидуальную работу с учащимися,которые делятся на три группы:1)выполнили работу без ошибок,2)с единичными ошибками,3)не справились с работой.
Урок «Анализ контрольной работы» проходит следующим образом:
1).Устный счет-включены основные моменты теории и примеры,отрабатывающие их.
2).На экране показана выполненная контрольная работа с теми заданиями ,где допущены ошибки.
Учащиеся первой и второй групп находят ошибки у себя в тетради и с места комментируют решение. Эта часть работы проходит очень активно и заинтересованно,учащиеся стараются выяснить все непонятные вопросы.
3)Проводится мини-тест,который содержит задания с учетом ошибок,допущенных в контрольной работе.
4).Учащиеся,справившиеся с контрольной работой (3группы),помогают его проверять.
5).Разбираются вновь или повторно допущенные ошибки.
6).Проводится самостоятельная работа по индивидуальным карточкам.
Для учащихся,не усвоивших тему,проводится урок –консультация ,затем зачет,который включает вопросы и задания обязательных результатов обучения.
Практикую и такую форму урока:
Выдаю тетради без исправленных ошибок и оценок,(результаты проверки записаны в планах).На экране показываю подробное решение каждого варианта.Учащиеся карандашом исправляют ошибки,сопоставляя свои решения с решениями на экране.Те задания ,которые они решили полностью неверно или не решили,записывают в тетради для контрольных работ,затем ставят себе оценку за контрольную работу и сдают тетрадь. Те дети,которые справились с контрольной работой,решают задания повышенной сложности.Затем учащиеся еще раз просматривают решения заданий на экране и пишут самостоятельную работу.Оценка в журнал ставится с учетом проведенной работы над ошибками. Такая форма работы с учащимися позволяет не только ликвидировать пробелы в знаниях учащихся,но имеет и воспитательное значение.Ребята учатся добиваться цели,доводить дело до конца,отрабатывать навыки самостоятельной работы и четко организуют взаимопомощь.
М.Р.Семенихина.
Зачет в старших классах.
Практикую зачеты по геометрии: открытые и тематические.
Зачет состоит из двух частей:теоретической и практической.Вопросы зачета вывешиваю в самом начале изучаемой темы.Теоретическую часть учащиеся сдают устно. Практическая часть состоит из трёх задач. Класс делится на 4 группы. Каждому ученику дается своя карточка с обязательным и дополнительным заданием. Время на выполнение работы 30 минут,на проверку-10 минут,на подведение итогов-5 минут. Итоги подводят консультанты.
Такая форма организации зачёта даёт всем равные возможности для достижения хороших результатов. Хорошо успевающие учащиеся уже на этапе самостоятельной работы могут показать высокий результат.Далее они продолжают закреплять полученные знания,работая со своими группами. Остальные учащиеся имеют возможность сдать зачёт своим консультантам.
Меняя место зачёта в системе проверки знаний. Сначала предлагаю контрольную работу. Успешно справившихся с ней освобождаю от зачёта. Зачёт в основном сдают те,кто нуждался во время контрольной работы в дополнительном времени. Им оно предоставляется. С такими ребятами имею возможность побеседовать индивидуально и выявить пробелы в знаниях,которые тут же можно поправить.
Особый интерес представляют творческие зачёты по геометрии:”Решение одной задачи”,”Презентация темы”.
К 10-ому классу у учеников складывается определенная система знаний и умений,а в социальном плане появляется желание самоутвердиться. Такую возможность им предоставляет зачёт-экстерн. Например,при изучении темы “Круглые тела” ученики заранее знакомятся с планом работы: цилиндр,конус,контрольная работа,шар.К началу изучения темы “Цилиндр” и “Конус”,самостоятельно изучить тему “Шар” и приготовить презентацию.В ходе подготовки к зачёту планируются консультации. Для сдачи зачёта приходят учащиеся одной группы(4 человека).Каждый ученик отвечает теорию у доски,затем решает 2 задачи.Одна из них из предложенных к зачёту,другая-из дедактических материалов по геометрии.Информация о ходе сдачи зачёта показана в уголке. При такой форме организации зачёта каждый ученик имеет право выбора:работать со всем классом или изучать тему самостоятельно.
О проектах.(дополнение)
Важным аспектом в работе современного учителя является творческая активность и индивидуальные особенности каждого ребенка.Умение учащихся самостоятельно добывать знания и совершенствовать их намного важнее прочности приобретенных знаний.Приобщение учащихся к проектной деятельности и использование компъютерно-информационных технологий позволяет наиболее полно определять и развивать интеллектуальные и творческие способности.
В своей практике я использую метод проектов с 2010г. при изучении геометрии в 8-9 классах ,стереометрии,прикладных тем курса алгебры и начал анализа в 10-11 профильных классах.
В основу метода проектов положена идея о направленности учебно-познавательной деятельности учащихся на результат,который получается при решении практической или теоретически значимой проблемы.
Проектную деятельность учащихся начинаюс 9 класса,но подготовительная работа идет с 8 класса.
Первые проекты мои учащиеся делают в 8 классе по теме « Симметрия».При прохождении этой темы отмечается творческая активность и заинтересованность каждого ученика. На уроках активно формируются все ключевые компетенции.Активная форма организации труда позволяют поддерживать интерес к предмету. Практикую групповые и индивидуальные проекты.
Проекты в старших классах учащиеся выполняют в виде творческих работ-компъютерных презентаций.Это индивидуальные проекты.
Цель проектной деятельности:создание образовательной среды,способствующей формированию опыта проектной деятельности учащихся.
Задачи:
-формировать интересы,склонности учащихся к познавательной деятельности,практические умения и навыки проведения проектной деятельности
-развивать интерес и память
-развивать умение самостоятельно мыслить и использовать это умение на практике
-развивать способность излагать и защищать собственную точку зрения по проблеме
-способствовать мотивированному выбору своей деятельности и социальной адаптации учащихся.
Положительные моменты: учащиеся лучше усваивают материал,уроки стали интереснее,используют свои знания и умения,полученные на уроках ИКТ.
Мотивация обучения:интерес к предмету,к практическому материалу.
Работы по теме : «Многогранники» отражают развитие теории многогранников,знакомят с разнообразным миром многогранников,содержат фотографии моделей ,сделанных руками учащихся. «Симметрия»-содержат сведения о симметрии фигур на плоскости,симметрии для пространственных тел,симметрию в природе,в архитектуре,в убранстве и узорах различных музеев и памятников архитектуры.В 10-м классе на уроке по теме «Применение производной» учащиеся создали проект-компъютерную презентацию «Применение производной в физике и технике».
Работа над проектами проходит в 3 этапа:
1)Организационный:выбор темы,подбор литературы.
2)Основной:составление плана,подбор материала,решение задач.
3)Заключительный:оформление работ,презентация,защита презентации.
При защите презентации учащиеся демонстрируют и комментируют глубину разработки поставленной проблемы,ее актуальность. Одноклассники с интересом смотрят рабоы друг друга и оценивают их.
В данный момент идет пополнение методической копилки уроков и внеклассных мероприятий с использованием ИКТ и проектных работ учащихся,распространение опыта в работе с учащимися других классов.
Просмотр содержимого презентации
«Пирамида-Неволин, Муратова»


Пирамида - многогранник, состоящий из плоского многоугольника, точки, не лежащей в плоскости этого многоугольника и всех отрезков, соединяющих эту точку с точками многоугольника.
Данная точка называется вершиной пирамиды, а плоский многоугольник - основанием пирамиды. Ребрами называются отрезки, соединяющие вершину пирамиды с вершинами основания. Высотой называют перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Апофема - высота боковой грани правильной пирамиды.
АВСD - основание;
АВМ, ВСМ, СМD, АМD - боковые грани;
АМ , ВМ , СМ , DM - боковые ребра;
МО - высота;
МН - апофема.

Пирамиду, у которой в основании лежит правильный n-угольник , а основание высоты совпадает с центром основания называют правильной пирамидой. Осью правильной пирамиды называется прямая, содержащая её высоту.
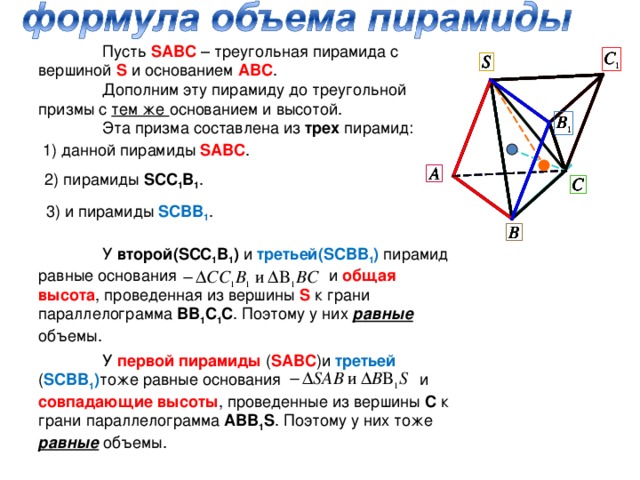
Пусть SABC – треугольная пирамида с вершиной S и основанием АВС .
Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой.
Эта призма составлена из трех пирамид:
1) данной пирамиды SABC .
2) пирамиды SCC 1 B 1 .
3) и пирамиды SCBB 1 .
У второй( SCC 1 B 1 ) и третьей( SCBB 1 ) пирамид равные основания и общая высота , проведенная из вершины S к грани параллелограмма ВВ 1 С 1 С . Поэтому у них равные объемы.
У первой пирамиды ( SABC )и третьей ( SCBB 1 ) тоже равные основания и совпадающие высоты , проведенные из вершины С к грани параллелограмма АВВ 1 S . Поэтому у них тоже равные объемы.
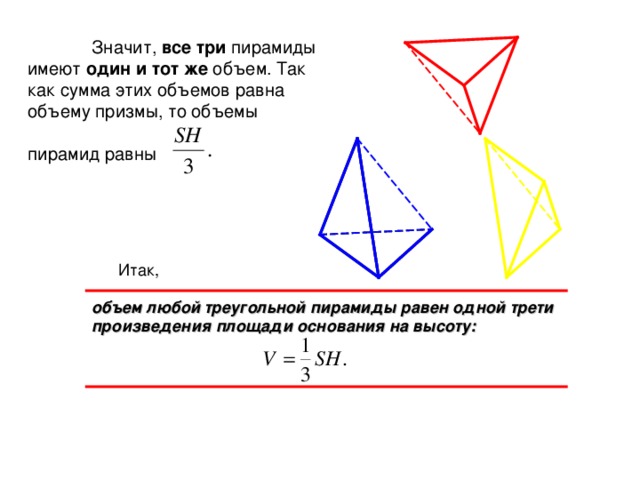
Значит, все три пирамиды имеют один и тот же объем. Так как сумма этих объемов равна объему призмы, то объемы
пирамид равны
Итак,
объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:

- Пусть теперь имеем любую, не обязательно треугольную
пирамиду.
- Разобьем ее основание на треугольники
3) Пирамиды, у которых основаниями являются эти треугольники, а вершинами – вершина данной пирамиды, составляют данную пирамиду.
4) Объем данной пирамиды равен сумме объемов составляющих ее пирамид. Так как все они имеют ту же высоту H , что и данная пирамида, то объем ее равен:
объем любой пирамиды равен одной трети произведения площади основания на высоту.

Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.
Объём пирамиды V=1/3h(S+S1+sqrt(S*S1)) где S1,S- площади оснований, h -высота

Самые величественные на сегодняшний день пирамиды — единственное из дошедших до нас семи чудес света — находятся в Гизе. Наиболее знаменита пирамида фараона Хуфу (по-гречески — Хеопса. Первоначально она была выстой 146.6 м. занимала площадь 5.2 га и весила как минимум 6.5 млн. т. Наполеон подсчитал, что затраченного на нее камня (более 2300 тыс. блоков) хватило бы на возведение вокруг Франции стены высотой 3 м и толщиной 30 см. Масштабы пирамиды соответствуют совершенству ее конструкции: все стороны основания имеют длину 2113 м (погрешность в пределах 20 см), а камни подогнаны так плотно, что между ними не просунуть и листа бумаги. Все грани пирамиды Хеопса с отклонением не более чем 4 градуса ориентированы по четырем сторонам света.



Просмотр содержимого презентации
«Презентация по геометрии Митькиной»
Презентацию подготовила
Ученица 11 «А» класса
МБОУ «СОШ №25»
Митькина Алена

Подобно тому как все искусства тяготеют к музыке,
все науки стремятся к математике.
Д. Сантаяна
- Геометрия есть искусство правильно рассуждать на неправильных чертежах.
Пойа Д.

Площадь
Площадь многоугольника- это положительная величина той части плоскости , которую занимает многоугольник.
Объем
Объем тела – это положительная величина той части пространства , которую занимает геометрическое тело.

Свойства объемов:
1. Равные тела имеют равные объемы
Свойства площадей :
1. Равные многоугольники имеют равные площади
F 2
F 2
F 1
F 1

2 . Если многоугольник составлен из нескольких многоугольников , то его площадь равна сумме площадей этих многоугольников.
S F =S F 1 +S F 2 +S F 3 + S F 4
2. Если тело составлено из нескольких тел , то его объем равен сумме объемов этих тел.
V F =V F 1 +V F 2
F 4
F 2
F 3
F 1
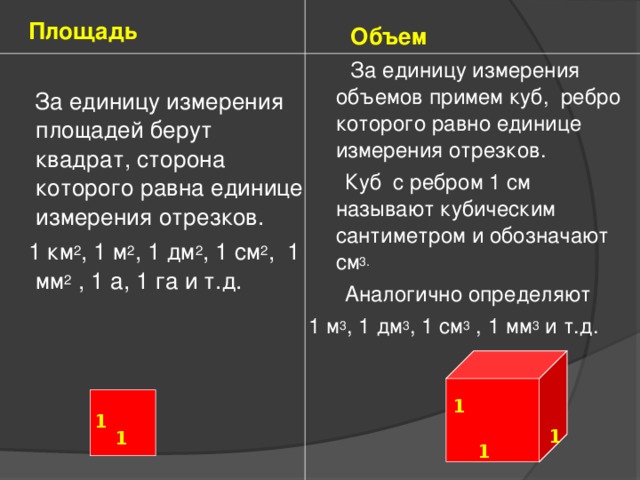
Площадь
За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков.
1 км 2 , 1 м 2 , 1 дм 2 , 1 см 2 , 1 мм 2 , 1 а, 1 га и т.д.
Объем
За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков.
Куб с ребром 1 см называют кубическим сантиметром и обозначают см 3.
Аналогично определяют
1 м 3 , 1 дм 3 , 1 см 3 , 1 мм 3 и т.д.
1
1
1
1
1
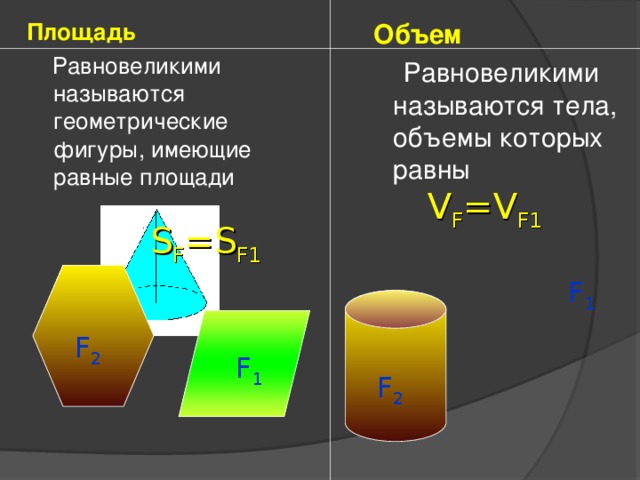
Площадь
Равновеликими называются геометрические фигуры, имеющие равные площади
Объем
Равновеликими называются тела, объемы которых равны
V F =V F1
S F =S F1
F 1
F 2
F 1
F 2
В стереометрии рассматриваются объемы многогранников и объемы тел вращения.
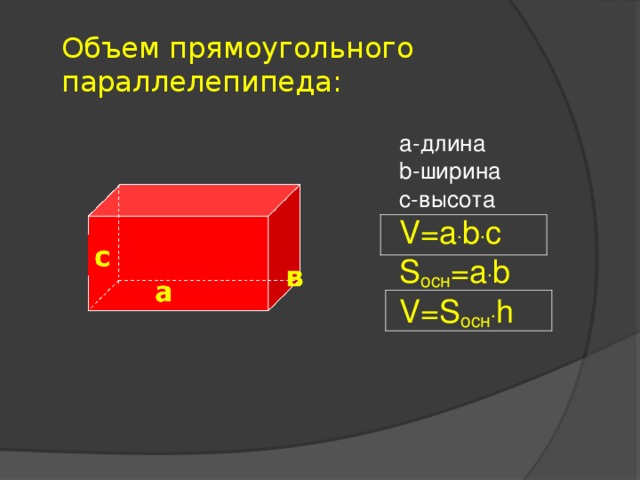
Объем прямоугольного параллелепипеда:
а-длина
b -ширина
с-высота
V=a . b . c
S осн = a . b
V=S осн . h
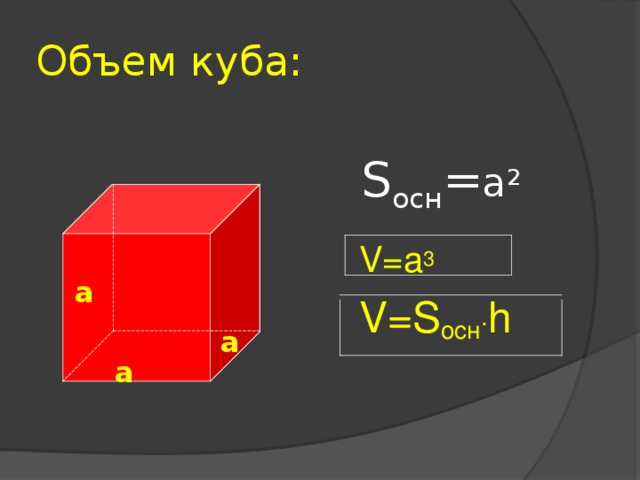
Объем куба:
V=a 3
V=S осн . h
S осн = a 2
а
а
а
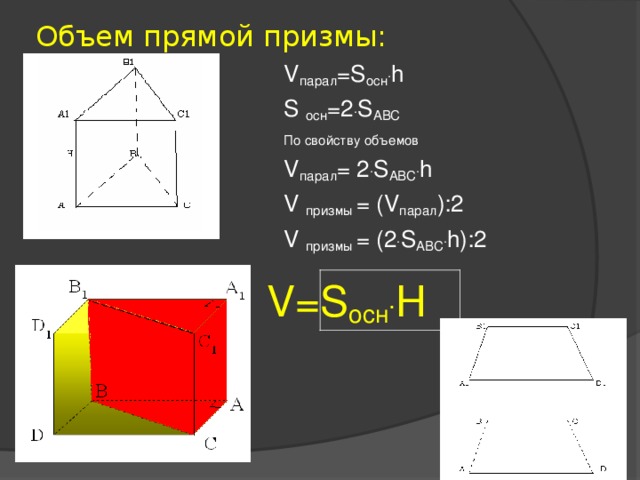
Объем прямой призмы:
V парал = S осн . h
S осн =2 . S ABC
По свойству объемов
V парал = 2 . S AB С . h
V призмы = ( V парал ):2
V призмы = ( 2 . S AB С . h) : 2
V=S осн . H

Объем пирамиды:
Достроим пирамиду
ABCS до призмы. Достроенная
призма будет состоять из 3
пирамид - SABC, SCC 1 B 1, SCBB 1
У 2 и 3 пирамиды- SC - общая,
тр CC 1 B 1 = тр CBB 1
У 1 и 3 пирамиды- С S- общая,
тр SAB = тр BB 1 S
V 1 =V 2 =V 3
V призмы= 3 V пирам
V пирамиды = 1 V призмы
3
V пирамиды = 1 S осн . H
3
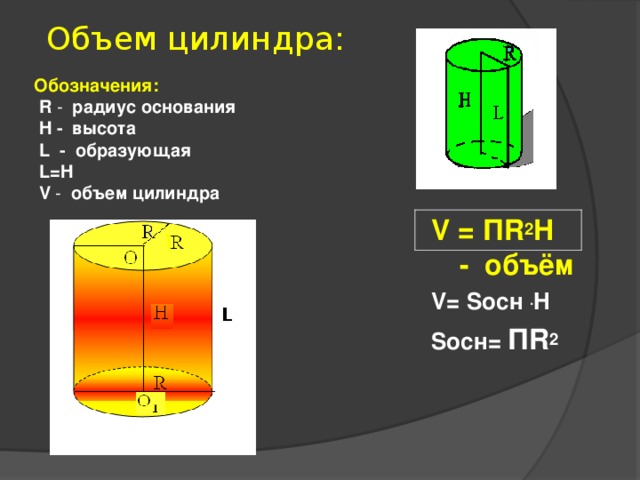
Объем цилиндра:
Обозначения:
R - радиус основания
H - высота
L - образующая
L=H
V - объем цилиндра
V = П R 2 H - объём
V= S осн . H
S осн = П R 2
L
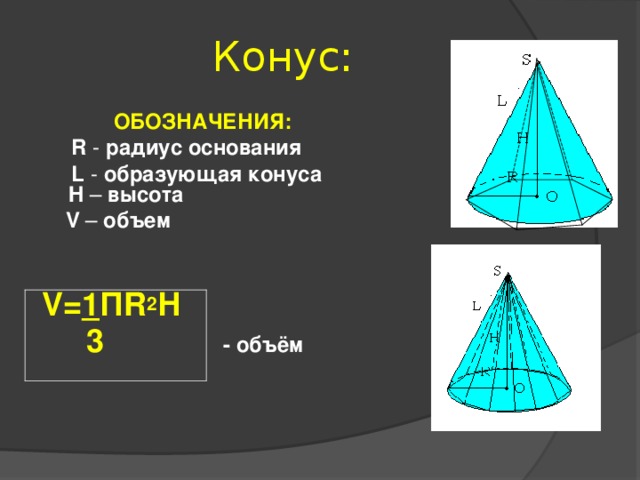
Конус:
ОБОЗНАЧЕНИЯ:
R - радиус основания
L - образующая конуса H – высота
V – объем
V= 1 П R 2 Н
3 - объём

Это интересно:
В геологии существует понятие "конус выноса". Это форма рельефа, образованная скоплением обломочных пород, вынесенных горными реками на предгорную равнину или в более плоскую широкую долину.
В биологии есть понятие "конус нарастания". Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
"Конусами" называется семейство морских молюсков подкласса пережнежаберных. Укус конусов очень опасен. Известны смертельные случаи.
В физике встречается понятие "телесный угол". Это конусообразный угол, вырезанный в шаре.
Просмотр содержимого презентации
«Цилиндр Вольман»


Определение цилиндра
Цилиндром называется тело, которое состоит из двух кругов , не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
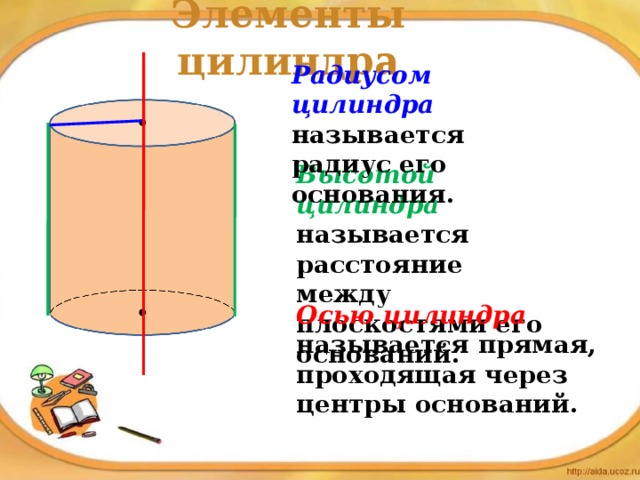
Элементы цилиндра
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Осью цилиндра называется прямая, проходящая через центры оснований.
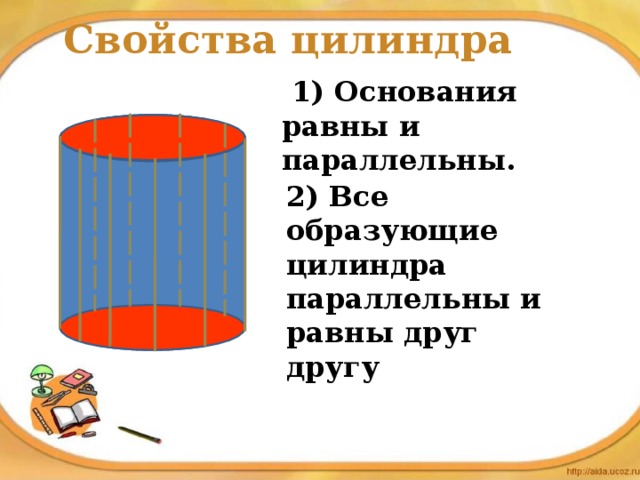
Свойства цилиндра
1) Основания равны и параллельны.
2) Все образующие цилиндра параллельны и равны друг другу
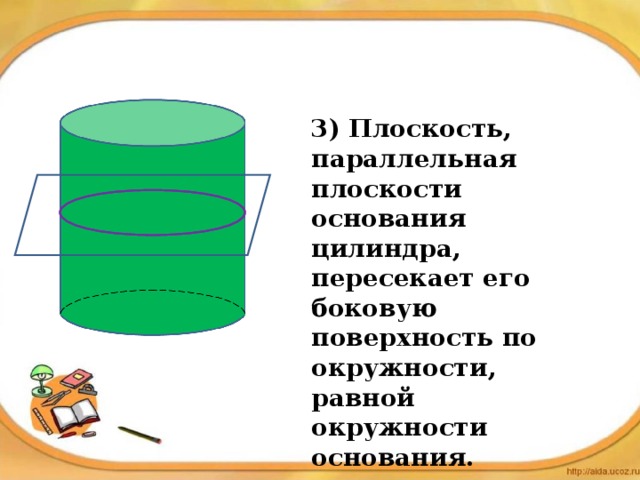
3) Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
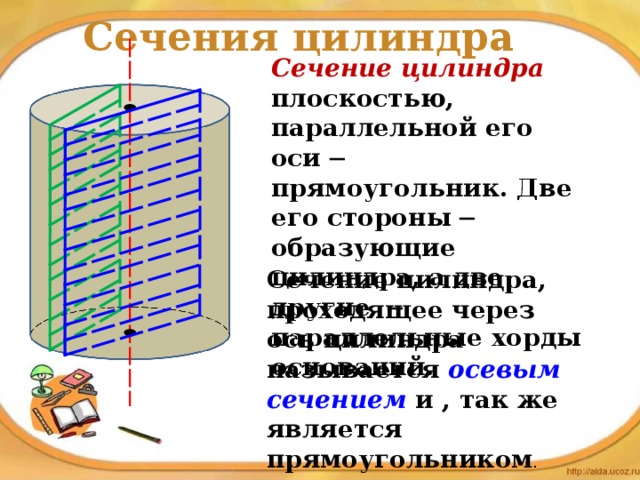
Сечения цилиндра
Сечение цилиндра плоскостью, параллельной его оси ─ прямоугольник. Две его стороны ─ образующие цилиндра, а две другие ─ параллельные хорды оснований .
Сечение цилиндра, проходящее через ось цилиндра называется осевым сечением и , так же является прямоугольником .

Объем цилиндра
Объем цилиндра вычисляется по формуле
h
V= П R 2 h
R
h – высота цилиндра
R – радиус основания

Доказательство
02.11.16

Площадь
Площадь боковой поверхности цилиндра можно посчитать по формуле
S бок = 2 П Rh
Площадь полной поверхности цилиндра просчитывается по формуле
S полн = 2 П Rh(h + R)
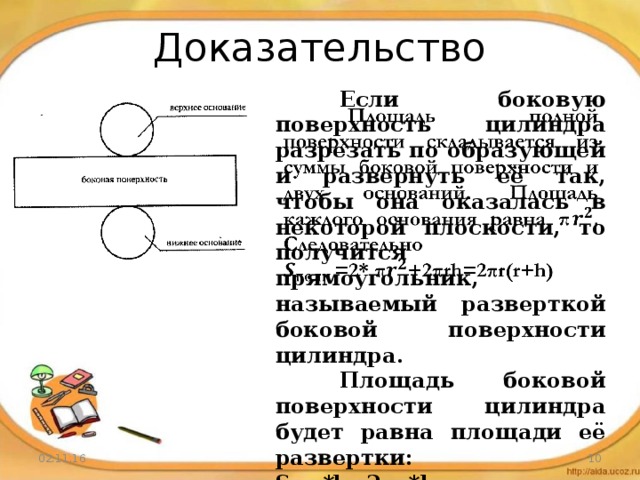
Доказательство
Если боковую поверхность цилиндра разрезать по образующей и развернуть её так, чтобы она оказалась в некоторой плоскости, то получится прямоугольник, называемый разверткой боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра будет равна площади её развертки:
S=a*b=2 π r * h
02.11.16
Просмотр содержимого презентации
«Объем шара и его частей»

Объем шара,
шарового сегмента,
шарового слоя,
шарового сектора.
Подготовил Сергеев Михаил 11 «А»

Оглавление
Объем шара
Доказательство объема шара
Объем шарового сегмента
Объем шарового слоя
Объем шарового сектора

Объем шара
Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Объём шара радиуса R равен
Оглавление

Доказательство
Возьмём четверть круга радиуса R с центром в точке (R;0).
Уравнение окружности этого круга : , откуда .
Функция непрерывная, возрастающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:
Откуда ч.т.д.
Оглавление

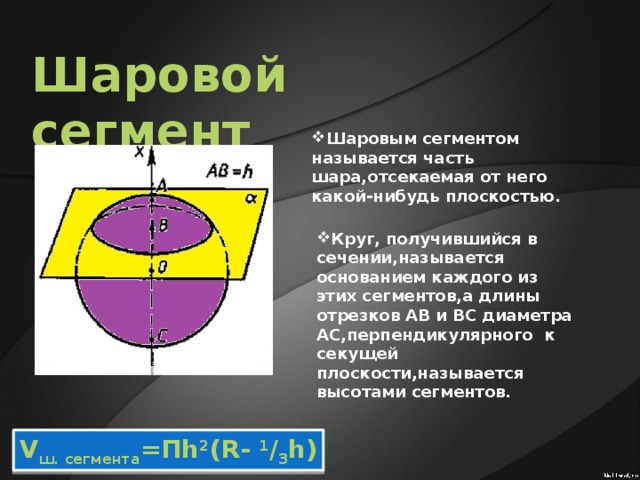
Объем шарового сегмента
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Объем шарового сегмента рассчитывается по формуле:
Оглавление

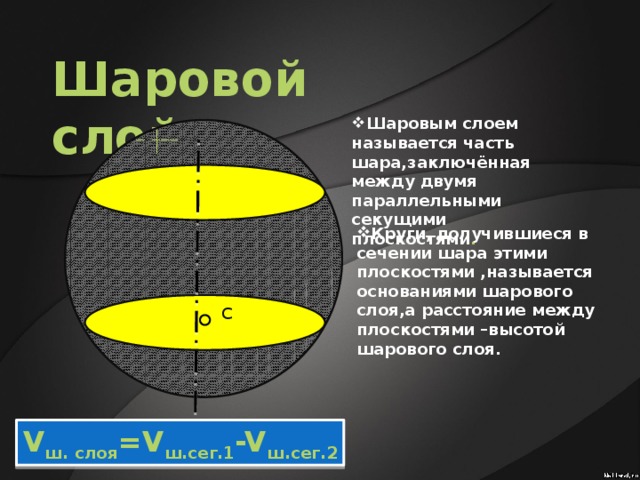
Объем шарового слоя
Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.
Круги, получившиеся в сечении шара этими плоскостями, называются основаниями шарового слоя.
Расстояние между плоскостями называется высотой шарового слоя .
Объем шарового слоя можно найти как разность объема двух шаровых сегментов:
где V — объем шарового слоя, H1 — высота большего шарового сегмента, H2 — высота меньшего шарового сегмента, R — радиус шара.
Оглавление
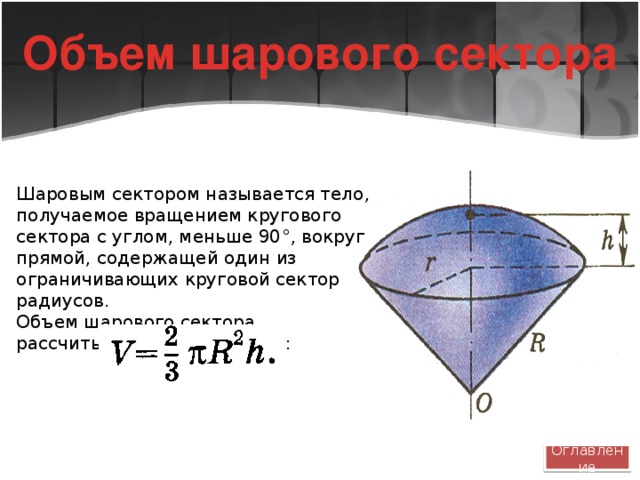
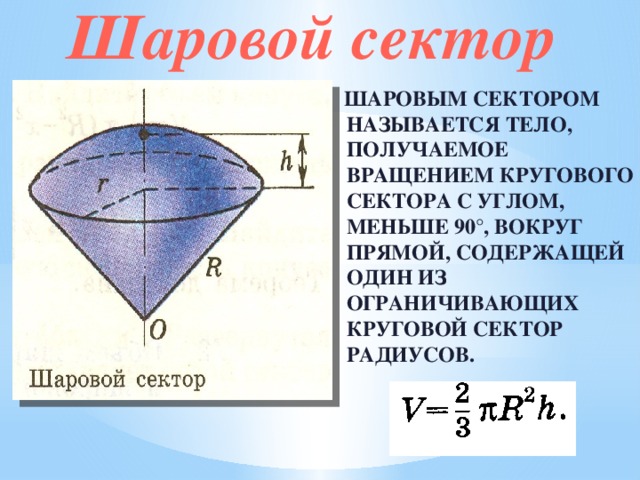
Объем шарового сектора
Шаровым сектором называется тело, получаемое вращением кругового сектора с углом, меньше 90 °, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Объем шарового сектора рассчитывается по формуле:
Оглавление

Объем шарового сектора
Оглавление

Спасибо за внимание!
Просмотр содержимого презентации
«Презентация по геометрии на тему- лДвижение. Виды движения¬ Выпо»

Презентация по геометрии на тему : «Движение. Виды движения» Выполнил ученик 9 «а» класса Шустиков Антон

Виды движения
- Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Виды движения :
Симметрия: Параллельный перенос
- осевая Поворот
- центральная
- скользящая
- зеркальная

История Симметрии
- Однако как люди дошли до такой сложной и одновременно такой простой вещи, как симметрия?
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин, который сейчас перешёл в русское слово «симметрия»
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.

Осевая Симметрия
Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси точку А1, при этом отрезок АА1, называется осевой симметрией .

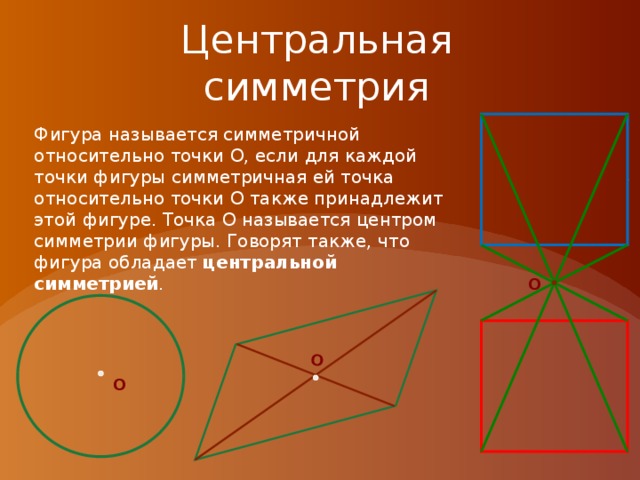
Центральная Симметрия
Преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией .

Скользящая симметрия
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Зеркальная симметрия
Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.

Роль симметрии в мире
- Собственно, как бы нам жилось без симметрии?
- Собственно, как бы нам жилось без симметрии?
- Собственно, как бы нам жилось без симметрии?
Точнее, какую роль играет симметрия в нашем мире? Неужели она лишь украшает его?
- Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром.
Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.

Симметрия в жизни
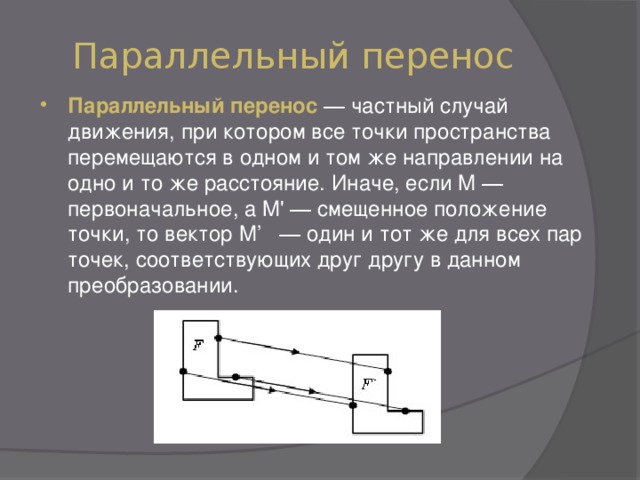
Параллельный перенос
- Параллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор M’ ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.
Пример параллельного переноса
Поворот
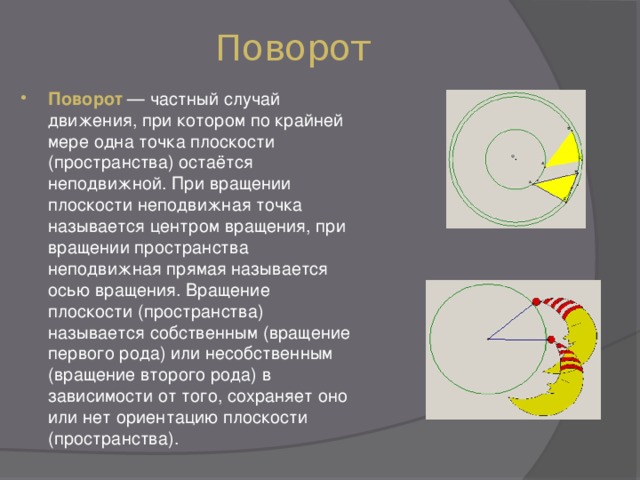
- Поворот — частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).

Заключение:
Движение и все его виды очень важны в нашей жизни. Без них не было бы тех архитектурных сооружений и технических достижений, что мы имеем.

Спасибо за внимание!
Просмотр содержимого презентации
«Симметрия»

Творческая работа
Симметрия.
Осевая и центральная
симметрии
Выполнила ученица 8«А» кл. Яковлева А.

Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность».
Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство.
Герман Вейль .
Что общего на данных рисунках?

а
Две точки и называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка и перпендикулярна к нему.
Прямая а называется осью симметрии.

Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
а
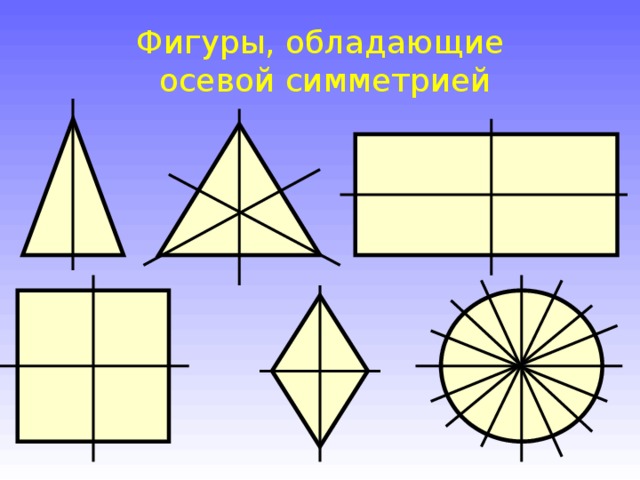
Фигуры, обладающие
осевой симметрией

Буквы, имеющие
горизонтальную ось симметрии
В Е Ж З К Н О С Ф Х Э Ю

Буквы, имеющие
вертикальную ось симметрии
А Д Ж Л М Н О П Т Ф Х Ш

Буквы, не имеющие
ось симметрии
Б Г И Р У Ц Ч Я Щ

Симметрия широко распространена в природе

Издавна человек использовал симметрию
в архитектуре

Две точки и называются симметричными относительно точки О, если О – середина отрезка .
Точка О – называется центром симметрии

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.