Комитет общего профессионального образования
Ленинградской области
ЛГУ им. А. С. Пушкина
Бокситогорский институт (филиал)
повышения квалификации
Итоговая работа на тему
«Приемы формирования личностных и метапредметных результатов при изучении темы «Площадь прямоугольника»»
Выполнили слушатели курсов повышения квалификации
по программе «ФГОС второго поколения. Новые подходы
в преподавании математики» Дворяк А. Ф.,
Юрченко Л. Р.,
Алябина Г. Ю.
2012
Теоретические основы обучения теме «Площадь прямоугольника»
ФГОС ООО применительно к школьному курсу математики.
ФГОС ООО представляет собой совокупность требований, обязательных при реализации основной образовательной программы основного общего образования образовательными учреждениями, имеющими государственную аккредитацию.
Стандарт выдвигает три группы требований: требования к результатам освоения основной образовательной программы ООО; требования к структуре основной образовательной программы ООО; требования к условиям реализации основной образовательной программы ООО.
Отличительной особенностью нового стандарта является его системно - деятельностный подход, ставящий главной целью развитие личности учащегося. В соответствии с предлагаемой моделью ключевым является ориентация на способность не заучивать, а применять знания, реализовывать собственные проекты, на овладение умениями коммуникации, анализа, понимания, принятия решений.
Поскольку в новой модели процесс обучения становится многообразным и вариативным, то важную роль начнет играть как внешняя, так и внутренняя система оценки качества, ориентированная на выявление и поддержку новых результатов, и распространение нового. В этой оценке должны найти место новые методы оценивания, которые будут отражать достижения и индивидуальный прогресс ребенка на уроке.
Стандарт устанавливает требования к результатам обучающихся, освоивших основную образовательную программу ООО, даёт разъяснение личностным, метапредметным и предметным результатам.
Изучение предметной области «Математика» должно обеспечить: осознание значения математики в повседневной жизни человека; формирование представлений о социальных, культурных и исторических факторах становления математической науки; понимание роли информационных процессов в современном мире; формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.
В результате освоения предметного содержания курса математики у учащихся формируются общие учебные умения и способы познавательной деятельности, обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию; получают представление об основных информационных процессах в реальных ситуациях.
Чтобы математические знания воспринимались учащимися как личностно значимые, т. е. действительно нужные ему, требуется постановка проблем, актуальных для ученика данного возраста, удовлетворяющих его потребности в познании. В организации учебно-воспитательного процесса важную роль играет сбалансированное соединение традиционных и новых методов обучения, использование технических средств. Для развития мотивационно-волевой сферы личности обучающегося в процессе обучения математике важно создавать ситуации, в которых он познаёт разнообразие математических отношений в реальной жизни, приобретает уверенность в своих силах при решении поставленных задач, развивает волю и настойчивость, умение преодолевать трудности. Содержание примерной программы по математике позволяет шире использовать дифференцированный подход к учащимся. Это способствует нормализации нагрузки обучающихся, обеспечивает более целесообразное их включение в учебную деятельность, своевременную корректировку трудностей и успешное продвижение в математическом развитии.
Цели обучения теме «Площадь прямоугольника»
За последние десятилетия в обществе произошли кардинальные изменения в представлении о целях образования и путях их достижения. В жизни каждого человека необходимостью и реальностью становится непрерывное образование. В общественном сознании происходит переход от понимания социального предназначения школы как задачи простой передачи знаний, умений и навыков от учителя к ученику к новому пониманию функции школы. Приоритетной целью школьного образования становится развитие у учащихся способности самостоятельно ставить учебные цели, проектировать пути их достижения, контролировать и оценивать свои достижения. Иначе говоря, формирование умения учиться. В связи с этим Стандартом второго поколения предусмотрено прежде всего формирование у учащихся универсальных учебных действий.
Выделяются четыре вида УУД: 1) личностные; 2) регулятивные; 3) общепознавательные; 4) коммуникативные.
Личностные универсальные учебные действия включают: смыслообразование, самооценивание, самопознание и самоопределение. Владение этими действиями позволяет ученику построить образ своего «Я», способствует личностному, профессиональному, жизненному самоопределению и построению жизненных планов во временной перспективе. Эта группа УУД направлена на установление учащимся значения результатов своей деятельности для удовлетворения своих потребностей, мотивов, жизненных интересов; установление связи между целью учебной деятельности и ее мотивом - определение того, «какое значение, смысл имеет для меня учение».
К регулятивным УУД относятся:
целеполагание (постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно);
планирование (определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий);
прогнозирование (предвосхищение результата и уровня усвоения, его временных характеристик);
контроль (сличение способа действия и его результата с заданным эталоном, с целью обнаружения отклонений и отличий от эталона);
коррекция (внесение необходимых дополнений и корректив в план, и способ действия в случае расхождения эталона, реального действия и его продукта);
оценка (выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения);
волевая саморегуляция, как способность к мобилизации сил и энергии, к волевому усилию в преодолению препятствий, эмоциональная устойчивость к стрессам, эффективные стратегии совладания с трудными жизненными ситуациями).
Общепознавательные УУД: общеучебные, логические, постановка и решение проблем.
К общеучебным УУД относятся: самостоятельное выделение и формулирование учебной цели; информационный поиск; знаково-символические действия; структурирование учебной информации и знаний; произвольное и осознанное построение устного и письменного речевого высказывания; смысловое чтение текстов различных жанров; извлечение информации в соответствии с целью чтения; рефлексия способов и условий действия, их контроль и оценка; критичность; выбор наиболее эффективных способов решения задач в зависимости от условий;
К логическим общепознавательным действиям относятся: анализ объекта с выделением существенных и несущественных признаков; синтез, как составление целого из частей, в том числе с восполнением недостающих компонентов; выбор оснований и критериев для сравнения, классификации, сериации объектов; подведение под понятие, выведение следствий; установление причинно-следственных связей; построение логической цепи рассуждения; выдвижение гипотез, их обоснование; доказательство.
Постановка и решение проблем включает: формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера.
Группа коммуникативных УУД включает: планирование учебного сотрудничества; постановку вопросов; построение речевых высказываний; лидерство и согласование действий с партнером.
Субъектный опыт.
Условием формирования личности, ориентирующейся в этом целостном мире, способной преобразовывать его и себя, является развитие человека как субъекта собственной жизненной стратегии. Становления субъектности у ребенка происходит очень рано и характеризуется формированием образа мира, отличающегося целостностью и личной к нему отнесенностью. Представить свойство субъектности и сделать его доступным изучению и даже диагностике удобнее через анализ более ощутимого образования – субъектного опыта», носителем которого является каждый ученик. Содержание учебной информации становится для ребенка личностно значимым только в том случае, когда оно воспринимается учеником через призму СО. «Научная информация дается через содержание учебного материала, при усвоении ученик «пропускает» ее через свой субъектный опыт и превращает в индивидуальные знания. Иного пути формирования знания просто нет». Поэтому, интеграция должна осуществляться в двух направлениях: интеграция общественно-исторического опыта, реализуемого в разных учебных предметах с сохранением специфики каждого, и интеграция общественно-исторического опыта и субъектного опыта учеников.
Целостность образовательного процесса, интеграция учебных предметов обеспечивается метаметодическим подходом. Понятие, термин которого знаком ребенку, может иметь субъективный смысл, отличный от научного, объективного. Но именно на этот субъективный смысл и будет опираться ученик, оперируя этим термином. Неучет СО часто приводит к тому, что учитель борется не с причиной, а с симптомами непонимания учениками учебного материала. Представление об окружающем мире как и любая информация, является субъективным образованием. Поэтому субъектный опыт является образовательной ценностью. Он включает такие составляющие, как:
содержательную (предметы, представления, понятия);
процессуальную (операции, приемы, правила выполнения действий (умственных и практических));
эмоционально - ценностную (личностные смыслы, установки, нравственные стереотипы).
Структурно СО представляет собой систему субъективных смыслов понятий, процессов, явлений, а также действий над ними, имеющих ценностную и эмоциональную окраску. Поэтому учет СО должен осуществляться на всех этапах учебно-воспитательного процесса. Особенно важно выявление субъектного опыта как в начале (исходный уровень), так и в конце урока (темы).
Площадь.
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. (Википедия)
Площадь — величина, измеряющая размер поверхности.
В математике
Площадь фигуры — геометрическое понятие, размер плоской фигуры.
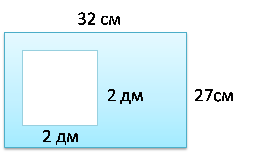
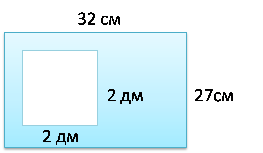
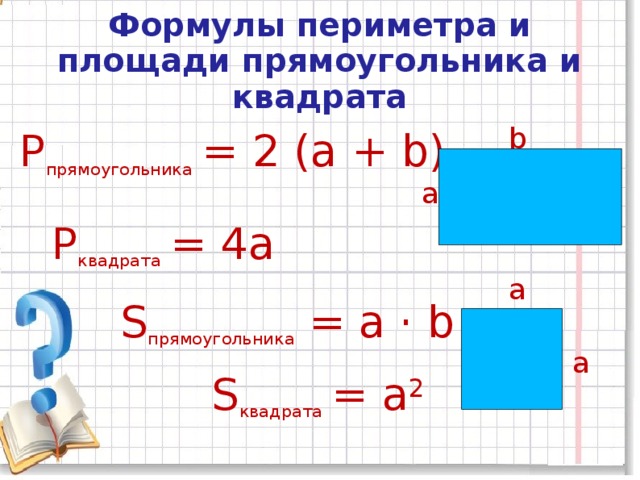
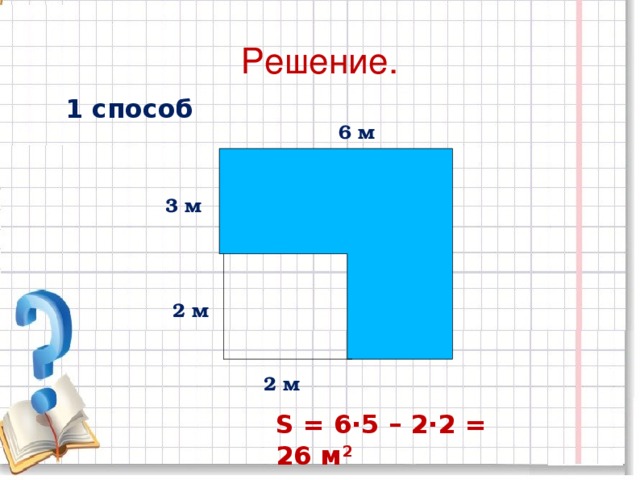
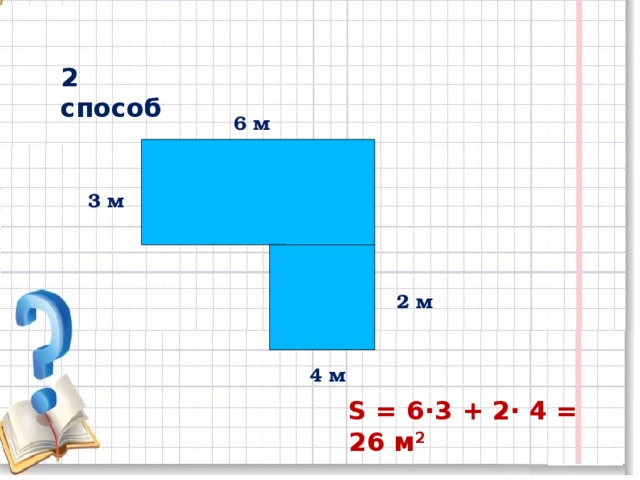
Площадь - одна из количественных характеристик плоских геометрических фигур и поверхностей. Площадь прямоугольника равна произведению длин двух смежных сторон. Площадь ступенчатой фигуры (т. е. такой, которую можно разбить на нескольких примыкающих друг к другу прямоугольников) равна сумме площади составляющих ее прямоугольников. Площадь любой плоской фигуры определяется как общий предел вписанных в нее или описанных около нее ступенчатых фигур. Для неплоских фигур (поверхностей) площадь определяют путем приближения их фигурами, состоящими из частей плоскости.
Площадь поверхности — числовая характеристика поверхности.
Площадь - Величина чего-нибудь, в длину и ширину, измеряемая в квадратных единицах
Площадь в архитектуре:
открытое пространство в городской застройке.
Площадь — открытое, обрамленное какими-либо зданиями или зелеными насаждениями пространство, входящее в систему других городских пространств, играет важную градостроительную роль. Среди наиболее известных площадей - Красная пл. в Москве, Дворцовая пл. в Санкт - Петербурге, пл. де Голля (б. пл. Звезды) в Париже.
Площадь - ж. ровное место. Европейская Россия одна площадь, особенно южная. Гора будто срезана, вершина площадью. Лес на площади растет, на плоскости, а не в горах. Площадь в городах или селеньях, незастроенный простор, шире улиц, майдан.
Площадь - Незаостренное большое и ровное место (в городе, селе), от которого обычно расходятся в разные стороны улицы
Жилая площадь
Площадь — деревня в Коношском районе Архангельской области.
Площадь - Пространство, помещение предназначенное для какой-нибудь цели
Площадь питания – поверхность участка (поля, сада и т.п.), занята одним растением, зависит от благоприятных особенностей культуры и сорта, возраста растений, условий возделывания, целей выращивания.
Историческая справка
Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников.
Определение понятия площади стали давать много позже.
Определения из учебников
А. В. Погорелов. Площадь простых фигур – положительная величина, численное значение которой обладает следующими свойствами:
1) Равные фигуры имеют равные площади.
2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей частей.
3) Площадь квадрата со стороной, равной единице измерения, равна единице.
Для других фигур площадь не определяется
А. П. Киселев, Н. А. Рыбкин. Величина части плоскости, ограниченной многоугольником или какой-нибудь другой плоской замкнутой фигурой, называется площадью этой фигуры
Свойства площадей и понятие об измерении площадей выделены отдельно
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина Площадь многоугольника – положительное число, обладающее следующими свойствами:
1) Равные многоугольники имеют равные площади
2) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников
Для произвольной фигуры площадь не определяется, а определяется только способ ее вычисления
А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Для многоугольных фигур площадью называется положительная величина с такими свойствами:
1) Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур
2) Равные фигуры имеют одну и ту же площадь
Для произвольной фигуры площадь не определяется, а определяется только способ ее вычисления
А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Площадью многоугольной фигуры называется положительная скалярная величина с такими основными свойствами:
1) Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур
2) Равные фигуры имеют равные площади
Определение дано в конце изучения темы «Площади»
В.Н. Руденко, Г.А. Бахурин. Определение не дается, но сформулированы аксиомы площадей:
1) Каждый многоугольник имеет положительную площадь
2) Площадь квадрата со стороной, равной единице длины, равна единице площади
3) Равные многоугольники имеют равные площади
4) Если многоугольник разбит на неперекрывающиеся многоугольники, то его площадь равна сумме площадей этих многоугольников
Отдельно дается определение площади круга: величина, к которой стремится площадь вписанного в его окружность правильного многоугольника при условии, что число его сторон неограниченно увеличивается
В.Г. Болтянский, Г.Д. Глейзер. Определение не дается, но сформулированы два основных свойства площади многоугольников:
1) Равные многоугольники имеют одну и ту же площадь
2) Если многоугольник представляет собой объединение нескольких многоугольников, попарно не имеющих общих внутренних точек, то площадь всего многоугольника равна сумме площадей его частей
Площадь криволинейной фигуры не определяется
Коллектив авторов. Математический энциклопедический словарь
Площадь – одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратиков
Свойства площадей выделены отдельно
Составитель – А.П. Савин. энциклопедический словарь юного математика
Площадью называется величина, характеризующая размер геометрической фигуры
Дан иллюстративный материал
И. М. Смирнова, В. А. Смирнов. Площадь фигуры - это число, показывающее, сколько раз единичный квадрат и его части укладываются в данной фигуре.
А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Для многоугольных фигур площадью называется положительная величина с такими основными свойствами:
1. Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур.
2. Равные треугольники имеют одну и ту же площадь.
И. Ф. Шарыгин. Площадь - это число, которое ставится в соответствие ограниченной плоской фигуре.
ПОЯВЛЕНИЕ ПОНЯТИЯ «ПЛОЩАДЬ»
Необходимость в понятии «площадь» возникла из жизненных потребностей.. В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе. Позже возникла потребность в измерении, сравнении разнообразных «фигур» (н.п. земельных участков). Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Площадь – открытое, архитектурно организованное, обрамленное какими-либо зданиями, сооружениями или зелеными насаждениями пространство, входящее в систему других городских пространств. Предшественниками городских площадей были парадные дворы дворцовых и храмовых.